Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Current page:

    Virtual Work Intro

    In the previous section, we discussed how to analyze a mechanism using DFA. As you may have noticed, it is a complicated process. Moreover, often we are not interested in the intermediate forces in a linkage; we are only interested in how the input forces affect the output forces. Virtual work gives us a relatively easy way to analyze the input and output forces of a linkage, focusing solely on external forces. A quick refresher of concepts applying to work and energy can be found here.

    Let's first review the Dot Product. The dot product is a vector that takes two vectors and returns a scalar. The dot product between two 2D vectors, \( \vec{a} \) and \( \vec{b} \), can be evaluated as:

    Dot Product
    $$ \begin{gather} \vec{a}=a_x\hat{i}+a_y\hat{j} \\ \vec{b}=b_x\hat{i}+b_y\hat{j} \\ \vec{a}\cdot\vec{b}=a_xb_x+a_yb_y=||\vec{a}||\,||\vec{b}||\cos{\theta}\end{gather} $$

    Note that \( \theta \) is the angle between the two vectors.

    Virtual work method

    Let's first start with the definition of work and power. Work for linear movement is defined as:

    Linear Work
    $$ W=\vec{F}\cdot\vec{d} $$

    and work for rotational movement is defined as:

    Rotational Work
    $$ W=\vec{\tau}\cdot\vec{\theta} $$

    Power is the time-derivative of work. Thus, the power for linear movement is:

    Linear Power
    $$ P=\frac{d}{dt}W=\vec{F}\cdot\frac{d}{dt}\vec{d}=\vec{F}\cdot\vec{v} $$

    and power for rotational movement is:

    Rotational Power
    $$ P=\frac{d}{dt}W=\vec{\tau}\cdot\frac{d}{dt}\vec{\theta}=\vec{\tau}\cdot\vec{\omega} $$

    If energy is conserved in a system, then we can write the following energy balance:

    Energy Balance
    $$ P_{in}=P_{out}+\frac{\partial}{\partial t}E_{system} $$

    A good way to think about this is a bucket with a hole at the bottom. We can fill the bucket with water, which is analogous to energy. The rate of water entering the bucket is equal to the rate of water leaving the bucket, plus the rate of change of the total amount of water in the bucket.

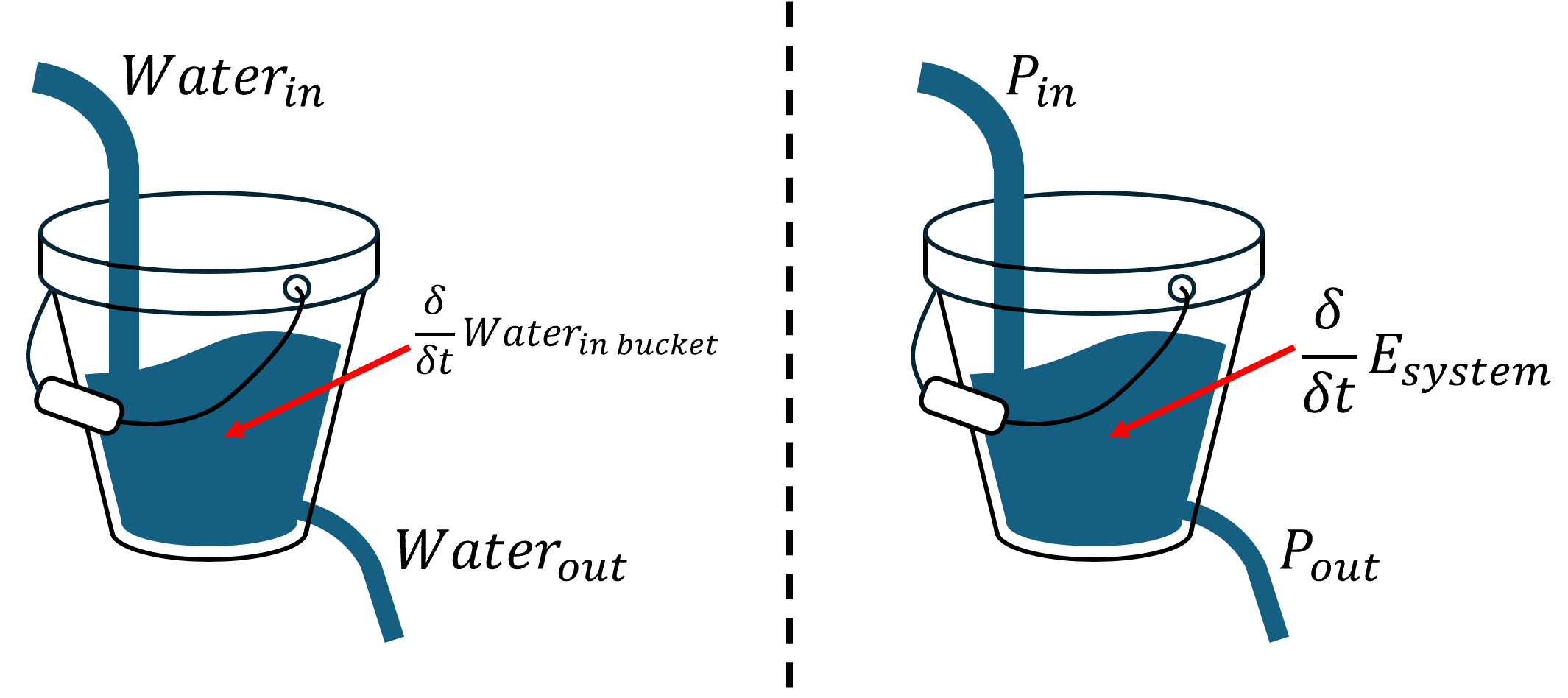
    Water bucket analogy for energy balance

    Moving back to mechanisms, we can compute the input power of a system by looking at the driving torque and angular velocity, which gives us the first term of the equation above. Then, if we know the rate of change in energy of the system, we can calculate the output power.

    First, two assumptions will be made to simplify analysis:

    1. The system's energy is composed only of kinetic and potential energy. i.e., there is no friction or other sources of energy loss.
    2. The system's kinetic energy is far greater than potential energy, so potential energy will be neglected. i.e., \( E_{system}=K_{system} \).

    Thus, the energy conservation equation becomes:

    Energy Conservation
    $$ P_{in}=P_{out}+\frac{\partial}{\partial t} K_{system} $$

    Expanding the kinetic energy term gives:

    Expanded Kinetic Energy
    $$ \frac{\partial}{\partial t} K_{system}=\frac{\partial}{\partial t}\sum_{i=0}^{n}\frac{1}{2} m_n v_n ^2= \sum_{i=0}^{n}m_n v_n \cdot a_n $$

    Rewriting the equation gives:

    VW Equation
    $$ P_{out}=P_{in}-\sum_{i=0}^n m_n v_n \cdot a_n $$

    With this in mind, if we know the input power and the velocity and acceleration of each component in the system, we can compute the output force or torque.

    In summary, the virtual work methods allow us to skip over the DFA process. Using only information about the input forces and the PVA data of a system, we can compute its output force and torque.