Current page:

Mass and Energy Balances

The rate of change of a system's internal energy is due to the net rate of energy input minus the net rate of energy output.

Closed System Energy Rate Balance

In the absence of mass flow, the closed system energy rate balance depends on the net heat flow rate $ \dot{Q}(t) $ and the net work transfer rate $ \dot{W}(t) $, as follows,

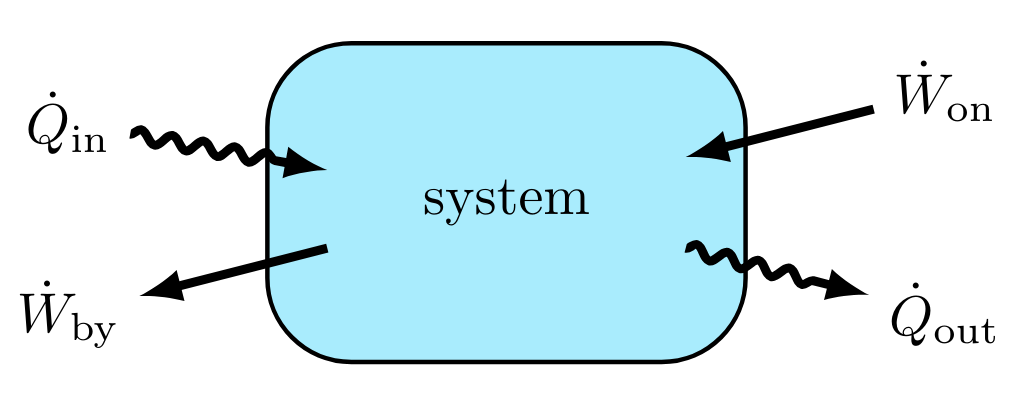
Change in internal energy differential eq. #deltaIE

$$ \frac{dU}{dt}=\dot{Q}(t)-\dot{W}(t), $$

Net Heat Flow Rate:

Comprised of the sum of the heat flow rates into the system minus the flow rates out of the system.

Net heat flow rate #dQdt

$$ \dot{Q}(t)=\dot{Q}_{\text{in}}(t)-\dot{Q}_{\text{out}}(t). $$

Net Work Transfer Rate:

Also known as net power transfer, where $ \dot{W}_{\text{by}} $ is the net work done by the system and $ \dot{W}_{\text{on}} $ is the net work done on the system.

Net work transfer rate #dWdt

$$ \dot{W}(t)=\dot{W}_{\text{by}}-\dot{W}_{\text{on}}. $$

Closed System Energy Rate Balance:

Here, $ \dot{Q}_{\text{in}} $, $ \dot{Q}_{\text{out}} $, $ \dot{W}_{\text{by}} $ and $ \dot{W}_{\text{on}} $ are explicitly defined as the magnitude of energy flow in the direction stated. The rate of change of the internal energy in the system is determined by combining Eqns. deltaIE, dQdt, and dWdt.

Change in internal energy explicit

$$ \begin{split}\frac{dU}{dt}&=\dot{Q}_{\text{in}}-\dot{Q}_{\text{out}}-(\dot{W}_{\text{by}}-\dot{W}_{\text{on}})\\&=\dot{Q}_{\text{in}}-\dot{Q}_{\text{out}}-\dot{W}_{\text{by}}+\dot{W}_{\text{on}}\end{split} $$

Closed System Energy Balance

The previous expression for the closed system energy balance can be determined by integrating the closed system energy rate balance (Eqn. deltaIE) with respect to time,

Change in internal energy result #intUdt

$$ \begin{split}U(t)-U(0)&=\int_0^t \dot{Q}(\tau)d\tau-\int_0^t \dot{W}(\tau)d\tau\\\Delta U(t)&=Q(t)-W(t).\end{split} $$

Energy Transfer via Mass Flow

Energy also transfers to or from a system during mass flow. For mass flow into a system, energy increases by the addition of both the internal energy of the additional mass and the $ pV $ work done by the mass on the system as it enters, and vice versa.

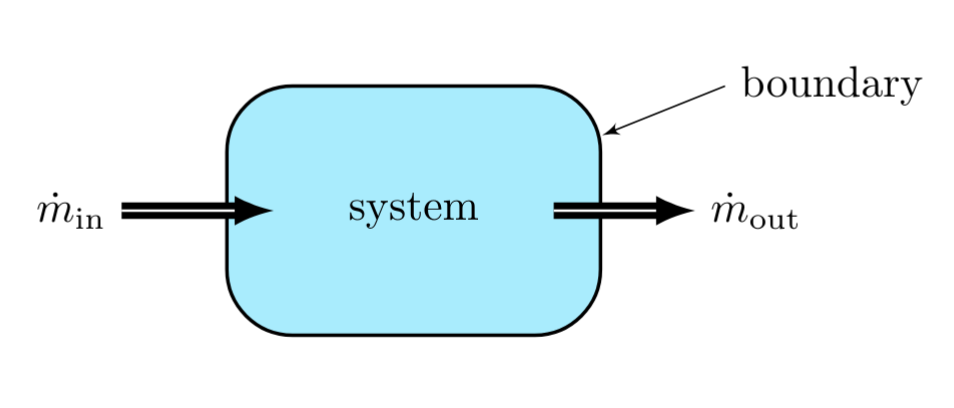
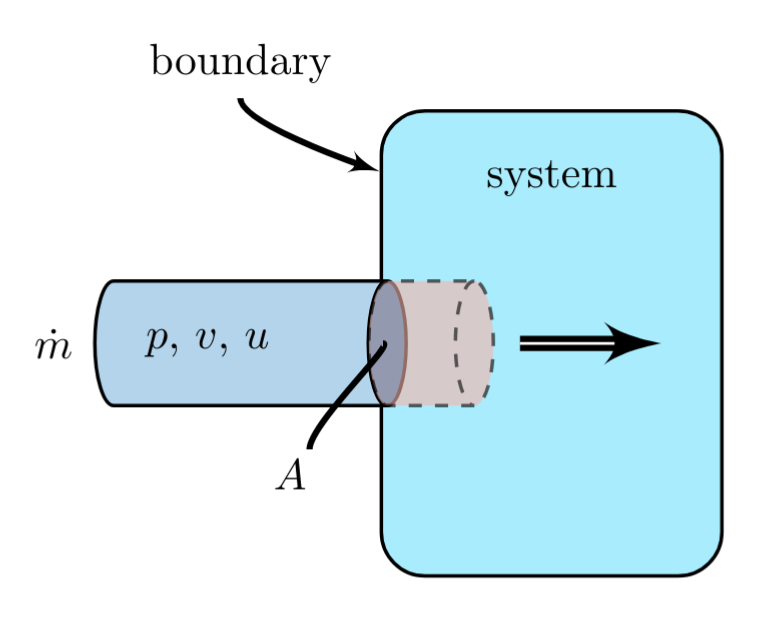
Internal Energy Change via Mass Flow

A mass flow having rate $ \dot{m} $ with cross-sectional area, $ A $, slowly enters a system. The mass is at a pressure $ p $, has a specific volume $ v $, and has a specific internal energy, $ u $, relative to some reference state.

The mass flowing into the system, over a given time interval $ \Delta t $, increases by the the internal energy the system as it enters, by:

Mass-flow & internal energy relationship #Deltau_dotm

$$ \dot{m}\Delta t u=mu. $$

$pV$ Work Done via Mass Flow

The volume occupied by the portion of the stream entering a system is defined by,

Volume in-flow

$$ V_{\text{in-flow}}=\dot{m}\Delta t v=mv $$

This volume is pushed at constant pressure, $ p $, into the system, doing $ pV $ work on the system,

Work due to volume in-flow #massflowPVwork

$$ W_{\text{in-flow}}=\int_{0}^{V_{\text{in-flow}}}p dV=mpv. $$

For an input stream with a constant specific volume $ v $ and pressure $ p $, taking the derivative of the above expression with respect to time yields the rate of work done on the system,

Change in work due to change in mass-flow

$$ \dot{W}=\dot{m}pv. $$

Total Internal Energy Change via Mass Flow

It follows that the total increase in the internal energy of the system includes the contributions of both Eqn. Deltau_dotm and Eqn. massflowPVwork.

Change in internal energy due to mass-flow

$$ \begin{split}\Delta U&=mu+mpv\\&=m(u+pv)\end{split} $$

The rate of internal energy increase is therefore,

Rate of change of internal energy #rateofDeltaU

$$ \frac{d U}{dt}=\dot{m}(u+pv) $$

Relative Specific Enthalpy

Recall, that the sum $ u+pv $ appears frequently in thermodynamic discussion so it is conveniently defined as relative specific enthalpy $ h $, consisting of the same atomic and molecular kinetic and potential energies as specific internal energy $ u $, but with the addition of flow work, $ pv $

Relative enthalpy #RelativeEnthalpy

$$ h=u+pv. $$

Internal Energy Rate Balance

In thermodynamic systems that experience both mass flow rates $ \dot{m}_{\text{in}} $ and $ \dot{m}_{\text{out}} $, net heat flow rate, $ \dot{Q} $, into the system, and performs work at a rate $ \dot{W} $ on its surroundings, a generalized energy rate balance can be used to describe all of these changes at once.

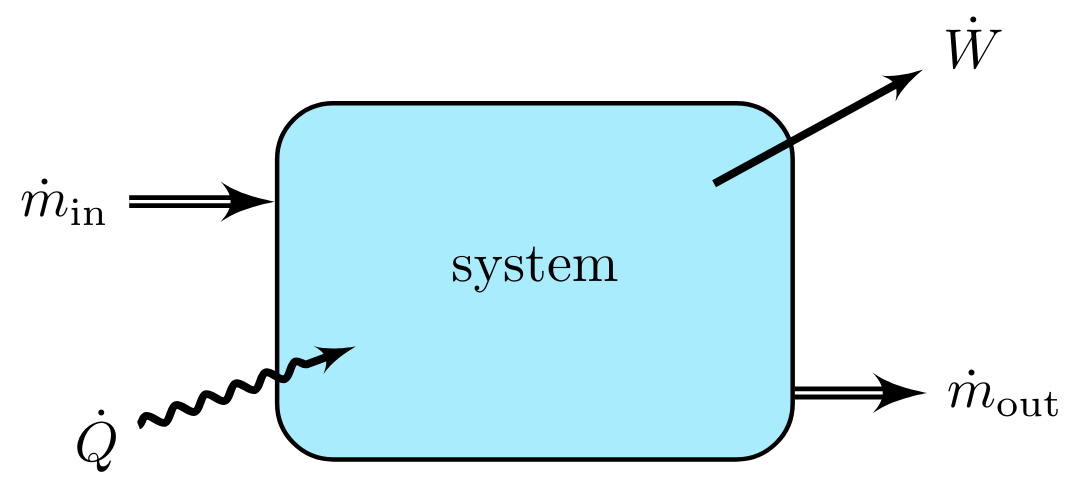
Recall that the rate of change of the internal energy of a system in the absence of mass flows is given by

Rate of change of internal energy without mass-flow

$$ \left.\frac{dU}{dt}\right|_{\text{no-flow}}=\dot{Q}(t)-\dot{W}(t) $$

Recall that the the mass flow rate `in` changes the internal energy of the system at a rate

Rate of change of internal energy due to mass-inflow #ROCofU_MFin

$$ \left.\frac{dU}{dt}\right|_{\text{in-flow}}=\dot{m}_{\text{in}}(u_{\text{in}}+p_{\text{in}}v_{\text{in}})=\dot{m}_{\text{in}}h_{\text{in}} $$

Similarly the mass flow rate `out` changes the internal energy at a rate

Rate of change of internal energy due to mass-outflow #ROCofU_MFout

$$ \left.\frac{dU}{dt}\right|_{\text{out-flow}}=-\dot{m}_{\text{out}}(u_{\text{out}}+p_{\text{out}}v_{\text{out}})=-\dot{m}_{\text{out}}h_{\text{out}} $$

The total rate of change in the internal energy is the sum of Eqns. ROCofU_woMF, ROCofU_MFin, and ROCofU_MFout, yielding a generalized equation to an arbitrary number of input and output streams yields

Rate of change of internal energy with mass-flow

$$ \frac{dU}{dt}=\dot{Q}-\dot{W}+\sum_{\text{in}}\dot{m}_{\text{in}}h_{\text{in}}-\sum_{\text{out}}\dot{m}_{\text{out}}h_{\text{out}} $$

Total Energy Balance

The kinetic and potential energy changes contribute to the total energy $ \Delta E $ of the system

Change in total energy

$$ \Delta E=\Delta U+ \Delta \text{PE}+ \Delta \text{KE} $$

Total Energy Rate Balance

The most general form of the energy rate balance $ \frac{dE}{dt} $

accounts for internal energy effects, along with kinetic and gravitational potential energy effects on the system via the total energy $ E $.

Rate of change of total energy

$$ \frac{dE}{dt}=\frac{d (\Delta U + \Delta KE + \Delta PE)}{dt} = \frac{dU}{dt}+\frac{d\text{KE}}{dt}+\frac{d\text{PE}}{dt} $$

This energy rate balance accounts for all energy contributions including kinetic and gravitational potential energy contributions to the system via mass inputs and outputs.

Rate of change of total energy expanded #ERateTotalGeneral

$$ \frac{dE}{dt}=\dot{Q}-\dot{W}+\sum_{\text{in}}\dot{m}_\text{in}(h_\text{in}+\frac{1}{2}\vec{v}_\text{in}^2+gz_\text{in})-\sum_{\text{out}}\dot{m}_\text{out}(h_\text{out}+\frac{1}{2}\vec{v}_\text{out}^2+gz_\text{out}) $$