Hydrostatic Fluid Pressure

Pascal's Law: A fluid at rest creates a pressure that is the same in all directions.

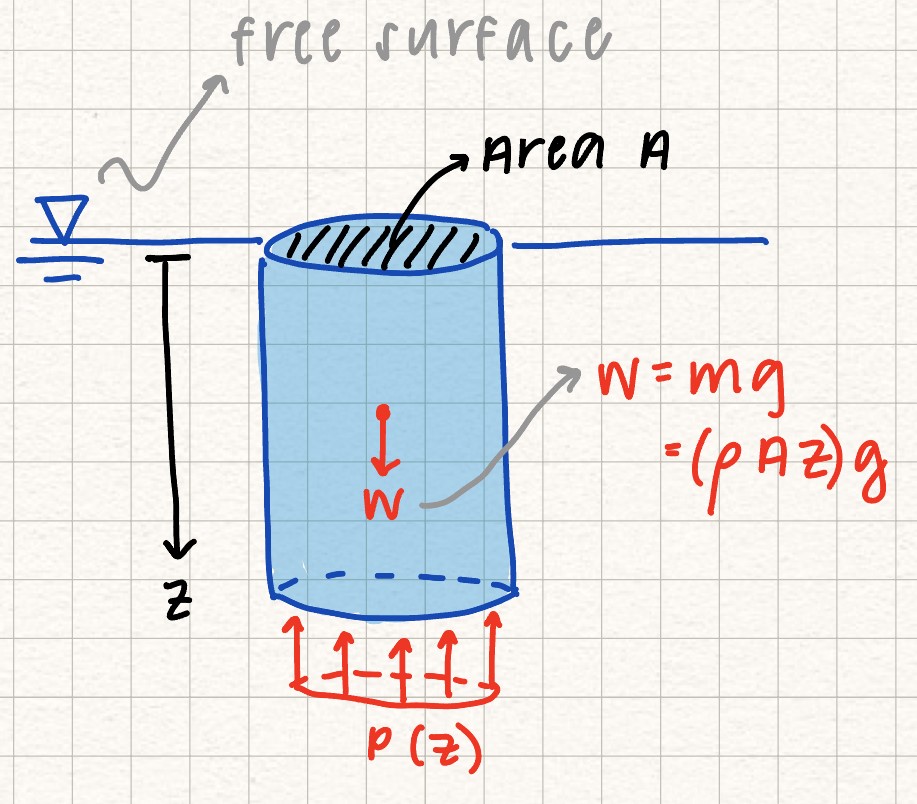
Hydrostatic Fluid Pressure: Hydrostatic fluid pressure refers to the pressure from a fluid that is at rest (the "static" part of hydrostatic). It orginates from the force of gravity acting on the fluid.

Fluid Pressure

For an incompressible fluid (density $ \rho $) at rest, the pressure $ P $ varies linearly with fluid depth $ z $. This means that the pressure along a horizontal plane (at a certain depth $ z $) is constant.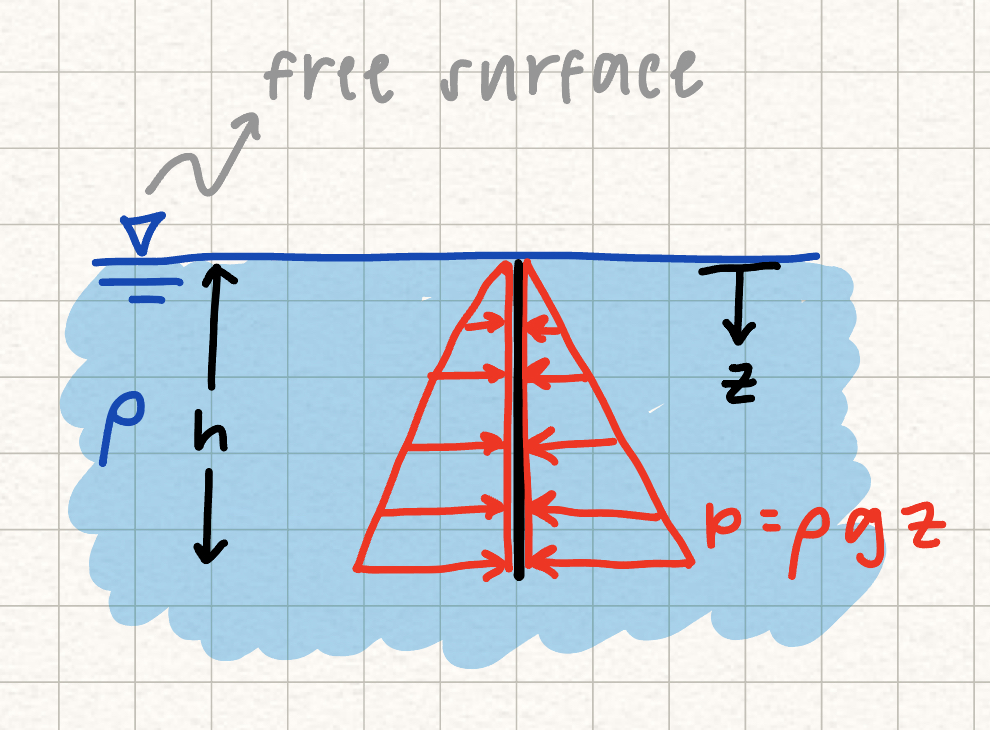

Derivation of the variation of pressure $ P(z) $ with respect to the fluid depth $ z $

The fluid pressure P(z) can be written as #hfp-eq

$$ P(z) = \rho*g*z $$

Ignoring air pressure:

$$ \begin{aligned} \sum{F_y} &= 0 \\ P(z)A - W &= 0 \\ P(z)A - (\rho \ A \ z) \ g &= 0 \\ P(z) &= \rho \ g \ z \end{aligned} $$

Warning: Don't confuse pressure with force! #force-pressure

Pressure is a force distributed over an area (force per area) and therefore has units of Pascals (Pa). To calculate the resultant force from hydrostatic fluid pressure, you must use

$$ F_R = P*A $$

where $ A $ is the area that the force is applied over.

Pressure, Distributed Loads, and Free Body Diagrams

Hydrostatic fluid pessure is a type of distributed load. If you need a refresher on distributed loads, see the Distributed Loads Reference Page.

Given a plate submerged in water, we can choose to draw the FBD of the plate in 2D or 3D:

In 3D, the value for $ w $, the distributed load on the plate from the fluid, is just the pressure $ P $ at depth $ h $. To solve for the resultant force from the distributed load we multiply by the area of the plate.

In 2D, the the value for $ w $, the distributed load on the plate from the fluid, is the pressure $ P $ at depth $ h $ multiplied by the plate depth $ b $. To solve for the resultant force from the distributed load we multiply by the length of the plate.

Fluid Pressure with Slanted and Curved Surfaces

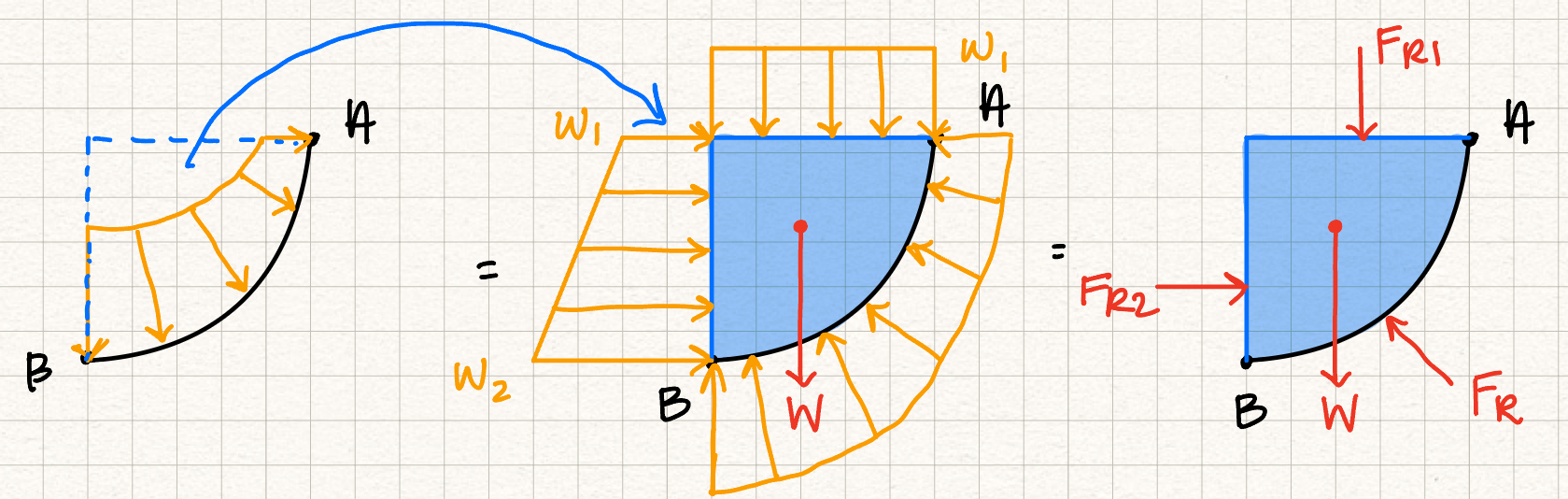
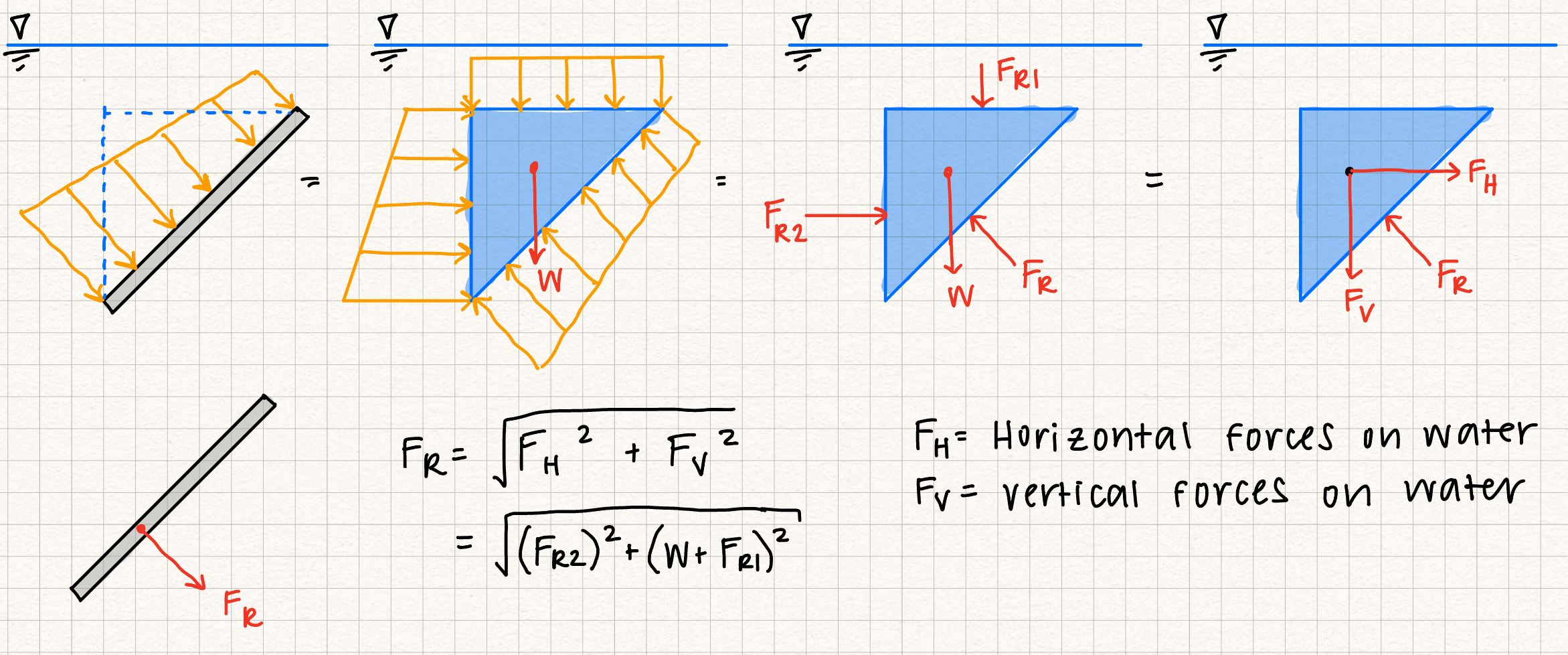
We will often be required to analyze the hydrostatic fluid pressure on surfaces that are not perfectly horizontal or vertical. In these cases, it is easier to redraw our system and create articifial horizontal and vertical "surfaces", adding the force from the FBD of the weight of the water trapped in our horizontal and vertical surfaces.

This method will result in the same resultant force on the slanted surface, but the distributed loads are easier to calculate.

Using this method, we can solve for the resultant force by calculating the total horizontal forces ($ F_H $) and vertical forces ($ F_V $) and relating them using

Resultant force from fluid pressure #res-force

$$ F_R = \sqrt{{F_H}^2+{F_V}^2} $$

Example Problem: Resultant force on a curved plate #fluid-curved

Find the magnitude of the resultant force from the fluid on the curved surface AB (thickness $ t $ of the surface $ = 2 \ m $). Density of $ \text{water} = 1000 \ kg / m^3 $

First, we will draw a FBD of the curved surface
This is complicated! Let's split into horizontal and vertical forces and look at the free body diagram of the water:
Solve for $ F_{R1} $ and $ F_{R2} $

$$ \begin{aligned} w_1 &= P_1 \ t = \rho \ g \ h_1 \ t \\ w_2 &= P_2 \ t = \rho \ g \ h_2 \ t \\ F_{R1} &= w_1 \ R = \rho \ g \ h_1 \ t \ R \end{aligned} $$

To solve for $ F_{R2} $, split the horizontal distributed load into a rectangle and a triangle:

$$ \begin{aligned} F_{triangle} &= \frac{1}{2} (w_2 - w_1) (R) \\ &= \frac{1}{2} \rho \ g \ (h_2 - h_1) \ t \ R \\ F_{rectangle} &= w_1 \ R = \rho \ g \ h_1 \ t \ R \end{aligned} $$

$$ \begin{aligned} F_{R2} &= F_{triangle} + F_{rectangle} \\ &= \frac{1}{2} \rho \ g \ (h_2 - h_1) \ t \ + \rho \ g \ h_1 \ t \ R \\ &= \rho \ g \ t \ R \ [\frac{1}{2} \ (h_2 - h_1) + h_1] \\ &= \rho \ g \ t \ R \ [\frac{1}{2} \ h_2 + \frac{1}{2} \ h_1 ] \\ &= \frac{1}{2} \rho \ g \ t \ R \ (h_2 + h_1) \end{aligned} $$
Solve for weight of water $ W $

$$ \begin{aligned} W &= m \ g = \rho \ V \ g \\ V &= \text{volume of water} = \frac{1}{4} \pi \ R^2 \ (t) \\ W &= \rho \frac{1}{4} \pi \ R^2 \ t \ g \end{aligned} $$
Solve for $ F_{H} $ and $ F_{V} $

$$ \begin{aligned} F_H &= F_{R2} \\ &= \frac{1}{2} \rho \ g \ t \ R \ (h_2 + h_1) \\ &= \frac{1}{2} (1000 \ kg/m^2) \ (9.81 \ m/s^2) \ (2 \ m) \ (3 \ m) \ (1.5 + 4.5 \ m) \\ &= 177 \ kN \end{aligned} $$

$$ \begin{aligned} F_V &= W + F_{R1} \\ &= \frac{1}{4} \rho \pi \ R^2 \ t \ g + \rho \ g \ h_1 \ t \ R = \rho \ t \ g \ R (\frac{1}{4} \pi \ R + h_1) \\ &= 1000 \ kg/m^3 \ (2 \ m) \ (9.81 \ m/s^2) \ (3 \ m) [ \frac{1}{4} \pi \ (3 \ m) + 1.5 \ m ] \\ &= 58,860*3.856 \\ &= 227 \ kN \end{aligned} $$
Solve for $ F_{R} $

$$ \begin{aligned} F_R &= \sqrt{{F_H}^2 + {F_V}^2} \\ &= \sqrt{{(177 \ kN)}^2 + {(227 \ kN)}^2} \\ &= 288 \ kN \end{aligned} $$

Buoyancy

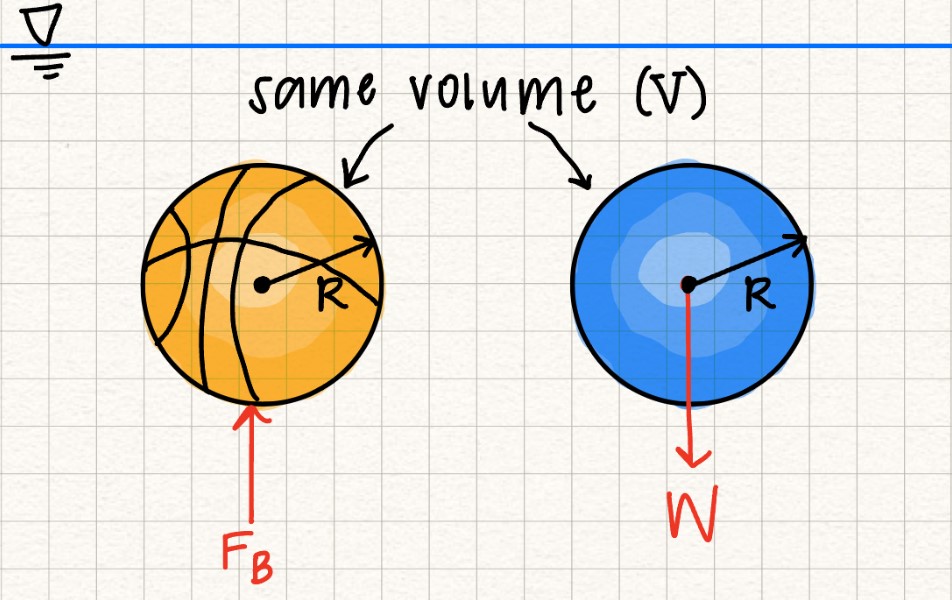
Archimedes' Principle: Any object that is either partially or totally immersed in a fluid has a buoyant force $ F_B $ equal to the weight of the fluid displaced by the object ($ W_{displaced} $).

Buoyant Force #buoyant-f

$$ F_B = W_{displaced} $$

$ \sum F_x : $ horizontal forces cancel out.

$$ \begin{aligned} \sum F_y : F_B &= F_{R_2} - F_{R_1} \\ &= w_2 \ S - w_1 \ S \\ &= \rho \ g \ h_2 \ S^2 - \rho \ g \ h_1 \ S^2 \\ &= \rho \ g \ S^2 \ (h_2 - h_1) \\ &= \rho \ g \ S^3 \\ F_B &= \rho \ g \ V = m \ g \end{aligned} $$

In which $ F_B $ is the buoyance force and $ \rho \ g \ V = m \ g $ is the weight of the volume of water displaced by the cube.

Example Problem: Buoyant force of a basketball #basketball

What is the buoyant force on this basketball with radius $ R $?

We know that the buoyant force is equivalent to the weight of the water that was displaced by the basketball, or the weight of a sphere of water that is the same size as the basketball.

$$ \begin{aligned} F_B &= W \\ &= m_{water} \ g \\ &= \rho_{water} \ V_{displaced} \ g \\ &= \rho_{water} (\frac{4}{3} \pi R^3) \ g \end{aligned} $$