Virtual work
In general, a force does work when it produces a displacement along its line of action. When we talk about virtual work, we're imagining those displacements becoming infinitesimally small.
Work is defined as positive when the force and the displacement are in the same direction, and negative when the force and displacement are in opposite directions.
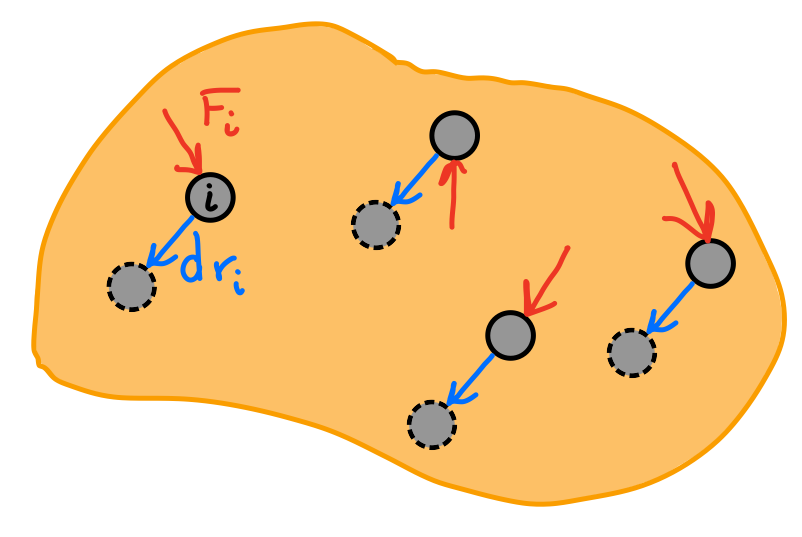
Virtual displacements
A virtual displacement is an infinitesimally small translation (\( dr \)) and/or rotation (\( d\theta \)) that is possible in the system.
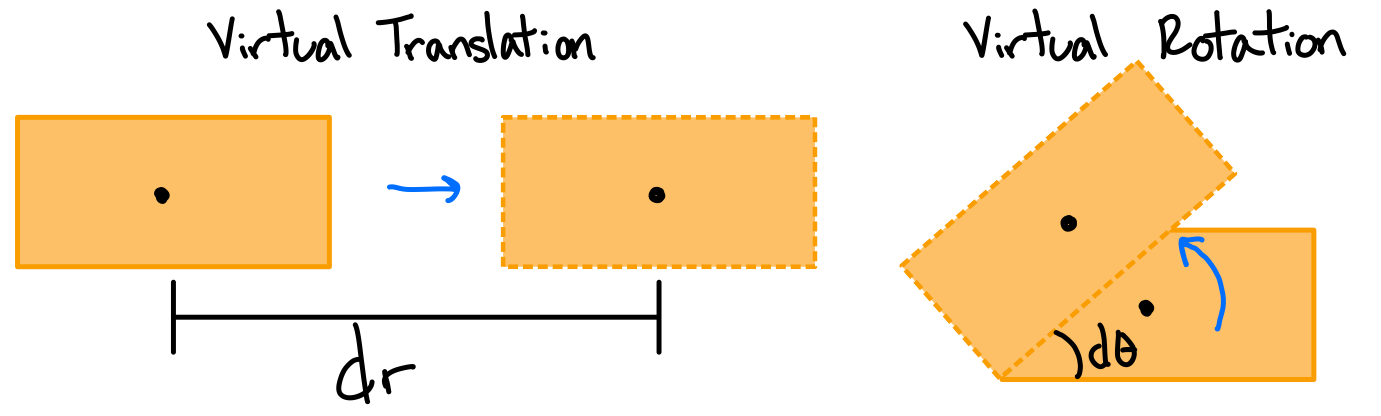
Note: virtual displacements are assumed to be possible, but don't actually exist.
Couple moments
Couple moments can also do work! When a body's rotation and the moment vector are oriented in the same direction, the couple moment does work. For 2D problems, this is when both the moment and the rotation are oriented in the \( \hat{k} \) direction using the right hand rule.
Couple moment virtual work (\( dU \)) is the work produced by a couple moment (\( M \)) over an infinitesimally small angular displacement (\( d\theta \)).
Principle of virtual work
If a body is in equilibrium, the sum of the virtual work done by all the forces and couple moments acting on the body is zero. We can use this principle to solve for the forces on systems.Virtual work analysis
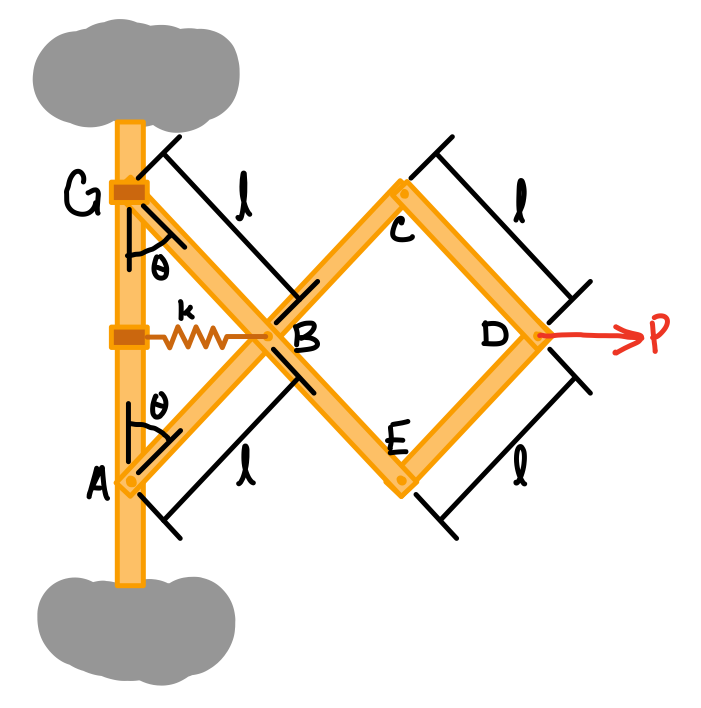
Steps for completing an analysis of a system using virtual work:
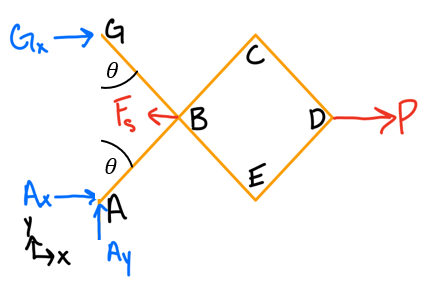
- Draw a free body diagram of the system, including a coordinate system.
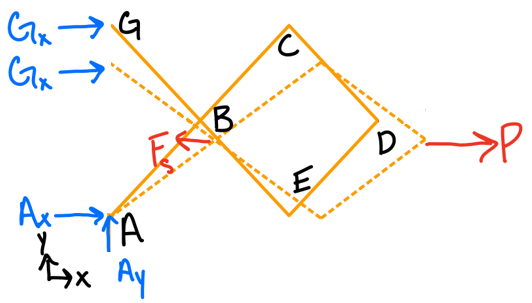
- Sketch the "deflected" position of the system.
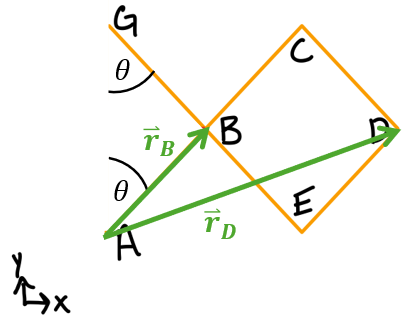
- Define the position coordinates (measured from a fixed point).
- Identify the components of the forces or moments that are parallel to the virtual displacements (the parallel line of action components).
- Remove all the forces that do not complete any work.
- Differentiate the position coordinates to obtain virtual displacement.
- Write the virtual work equation, expressing the virtual work of every force and moment.
- Factor out the common virtual displacement term (\( dr \) and/or \( dr \)) and solve.
We can use virtual work to solve for the forces in a system without needing to solve for all of the support reactions.
For example, if a truss is completely pinned on one end, it doesn't move, which means there is no virtual work completed on that pin because there are no virtual displacements (\( dr = 0 \)). This means that we can ignore it in our virtual work equation and don't need to solve for the reaction forces at the truss pin.