Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Current page:

    Energy Transfers

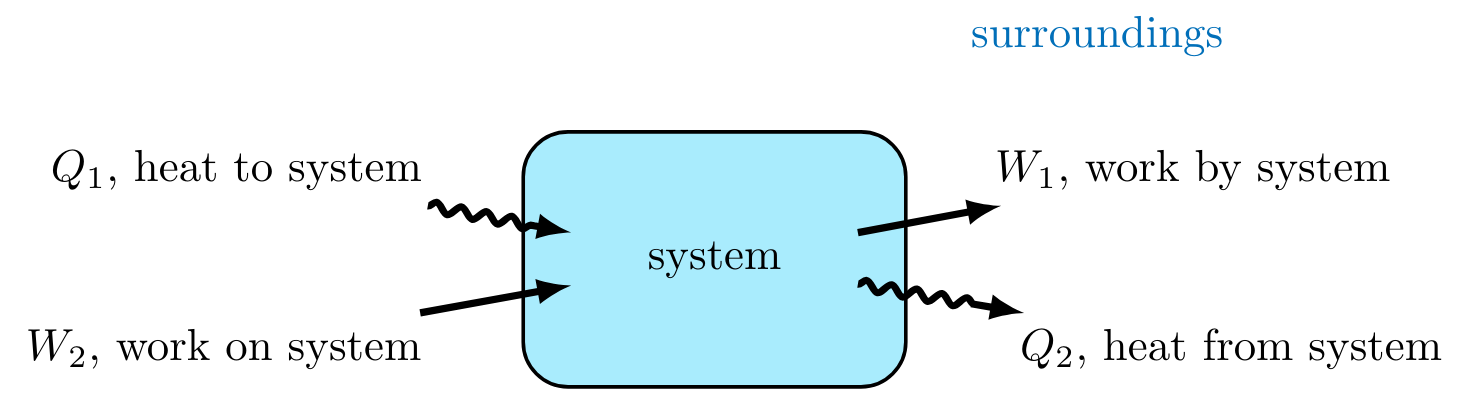
    When mass does not flow into or out of a system, the energy of the system changes in only two ways, through the loss or addition of work and/or heat.

    The internal energy (\( U \)) of a system is affected by the energetic contributions from heat flow (\( Q \)) in and out of a system and work (\( W \))done by or on a system.

    Energy balance equation #ebal
    $$ \Delta U = Q - W. $$
    Figure 1: A schematic illustrating the direction of energy flow when heat is transferred to/from the system and work is performed on or by the system.

    Heat

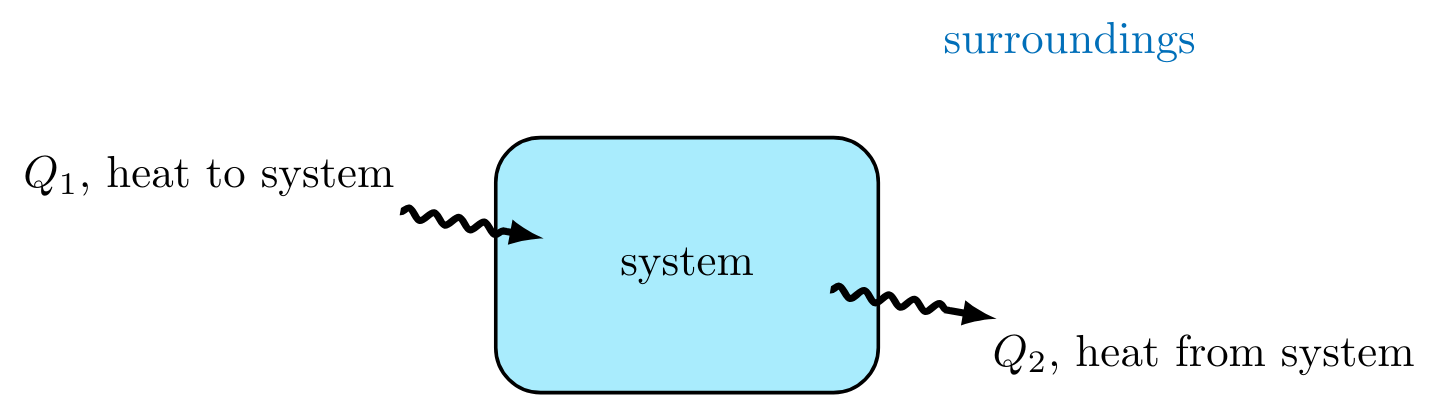
    In thermodynamics, heat \( Q \) is the thermal energy transferred between systems due to a temperature difference. Heat can both flow into and out of a system as shown in Figure 2.

    Figure 2: A schematic illustrating the heat flow transferred to/from the system.

    Work

    Recall from previous physics courses, that when a force \( f \) acts over a distance \( d \) it does work, defined as

    Linear work force-displacement relationship
    $$ W=fd. $$

    However, applied force does not have to be constant during a process. More generally, work is

    General work force-displacement relationship #genw
    $$ W=\int_{d_1}^{d_2}f(x)dx $$

    where \( f \) varies along the path parameterized by \( x \) from position \( d_1 \) to position \( d_2 \), where we are assuming \( f \) is tangent to the path.

    \(pV\) work

    Work done by or on a gas, is known as \( \boldsymbol{pV} \)~work. A gas, such as the one enclosed in the cylindrical device in Figure 3, applies a force uniformly over an area \( A \), due to collisions against the wall, which is defined as pressure,

    Pressure definition #pdefn
    $$ p=\frac{f}{A}. $$
    Figure 3: A sub-volume of gas, imparting forces from collisions on a sub-section of the container wall having area, \(A\).

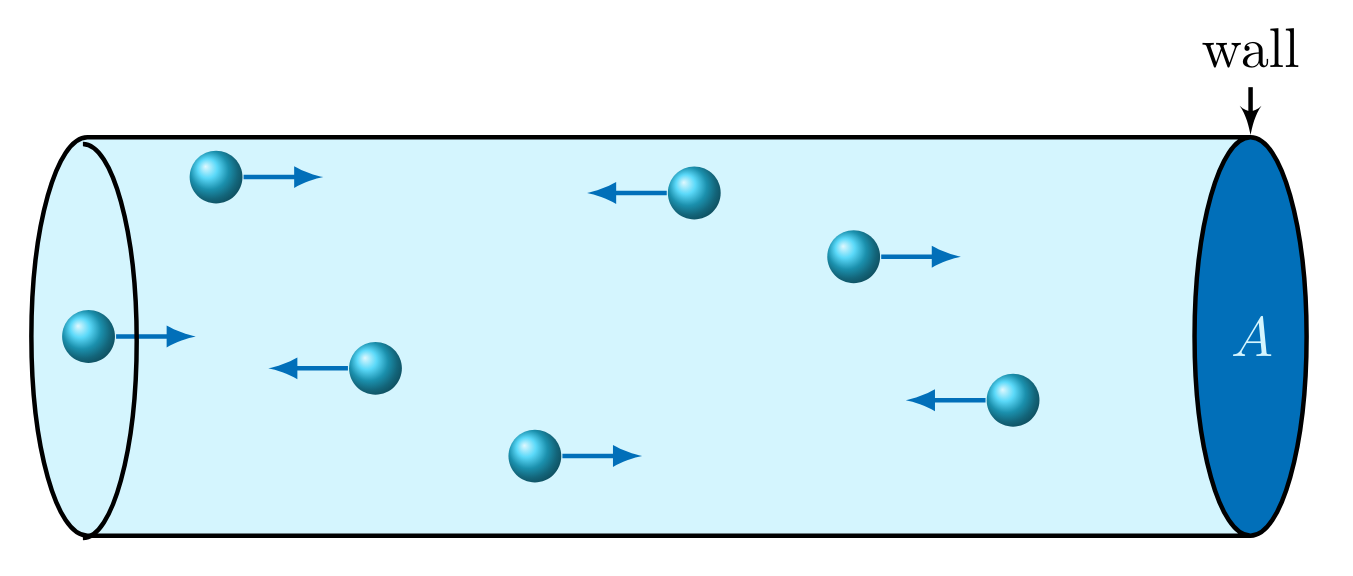
    Referring back to the definition of work in Eqn. GenW, if \( x \) is a single cartesian direction normal to an area \( A \) then \( A\cdot dx \) is a differential volume \( dV \). Additionally, using the definition of pressure Eqn. pdefn, we can define \( pV \) work as follows,

    \(pV\) work equation #pvwork
    $$ \begin{aligned} W &=\int_{d_1}^{d_2}f(x)\,dx \\ &=\int_{d_1}^{d_2}\frac{f(x)}{A}A,dx \\ &=\int_{V_1}^{V_2}p(V),dV \end{aligned} $$

    \( pV \) diagrams

    Graphs whose \( y \) and \( x \) axes are \( p \) and \( V \), respectively. According to the pV work equation, work is the area under the process curve. An example is shown in Figure 4.

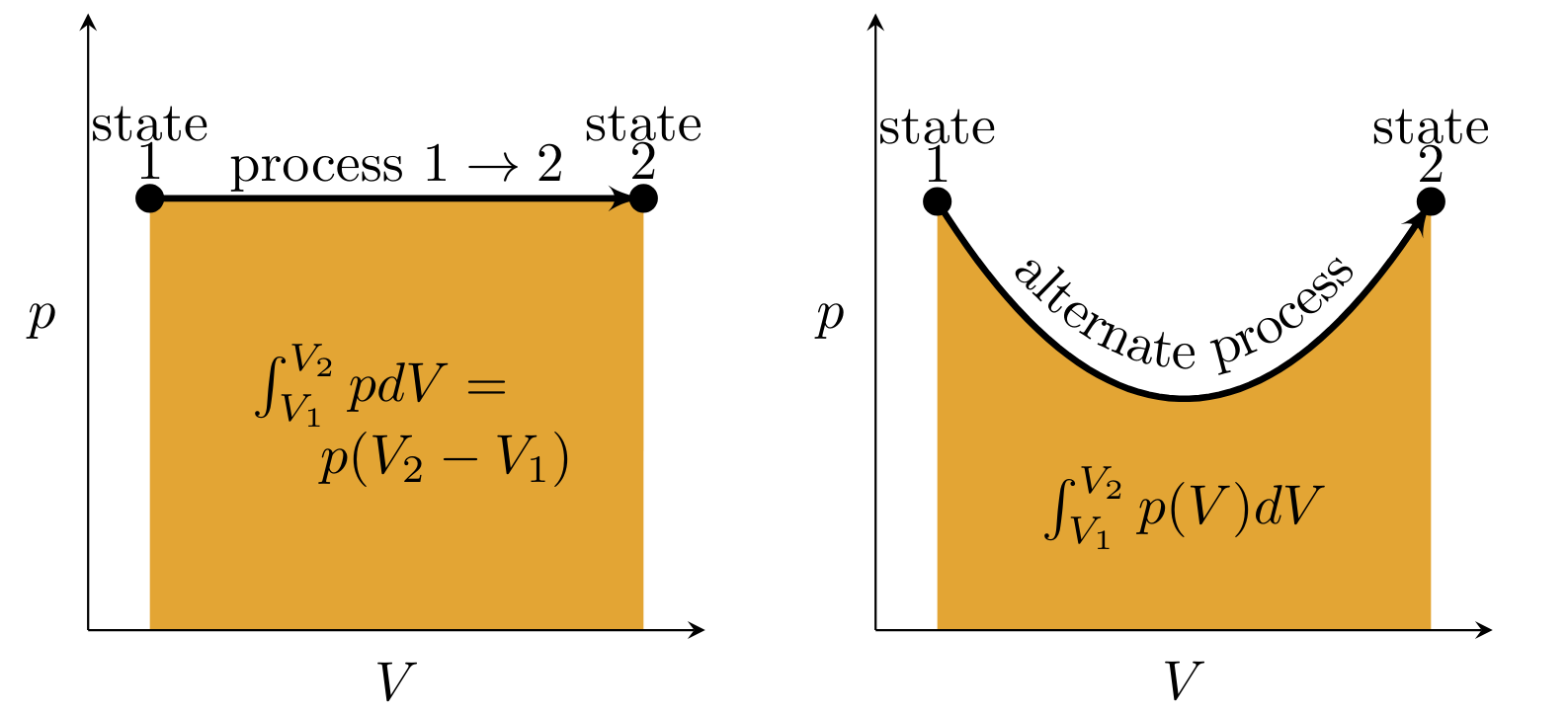
    Figure 4: \(pV\) diagrams for 2 processes where the start and end state are identical but with differing processes.

    Isobaric Process:

    During the process to go from 1 state to another, the system remains at a constant pressure, as shown in Figure 4 (left).

    Work is path dependent:

    Work transfer depends on the process. Figure 4 shows two processes where despite having the same initial and final thermodynamic states, the difference in magnitude of work for these two processes is different.

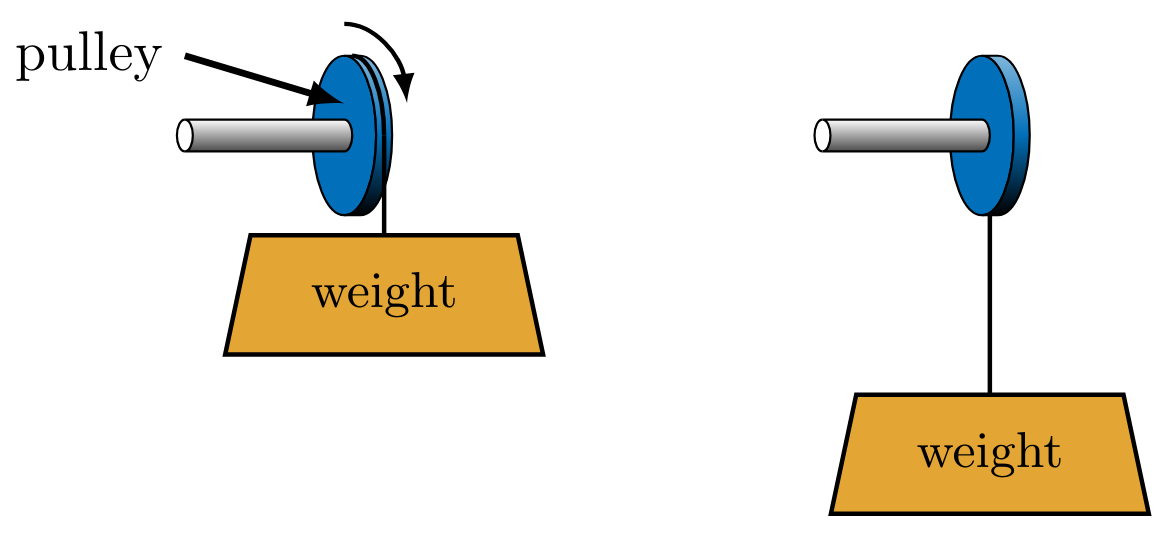
    Shaft work

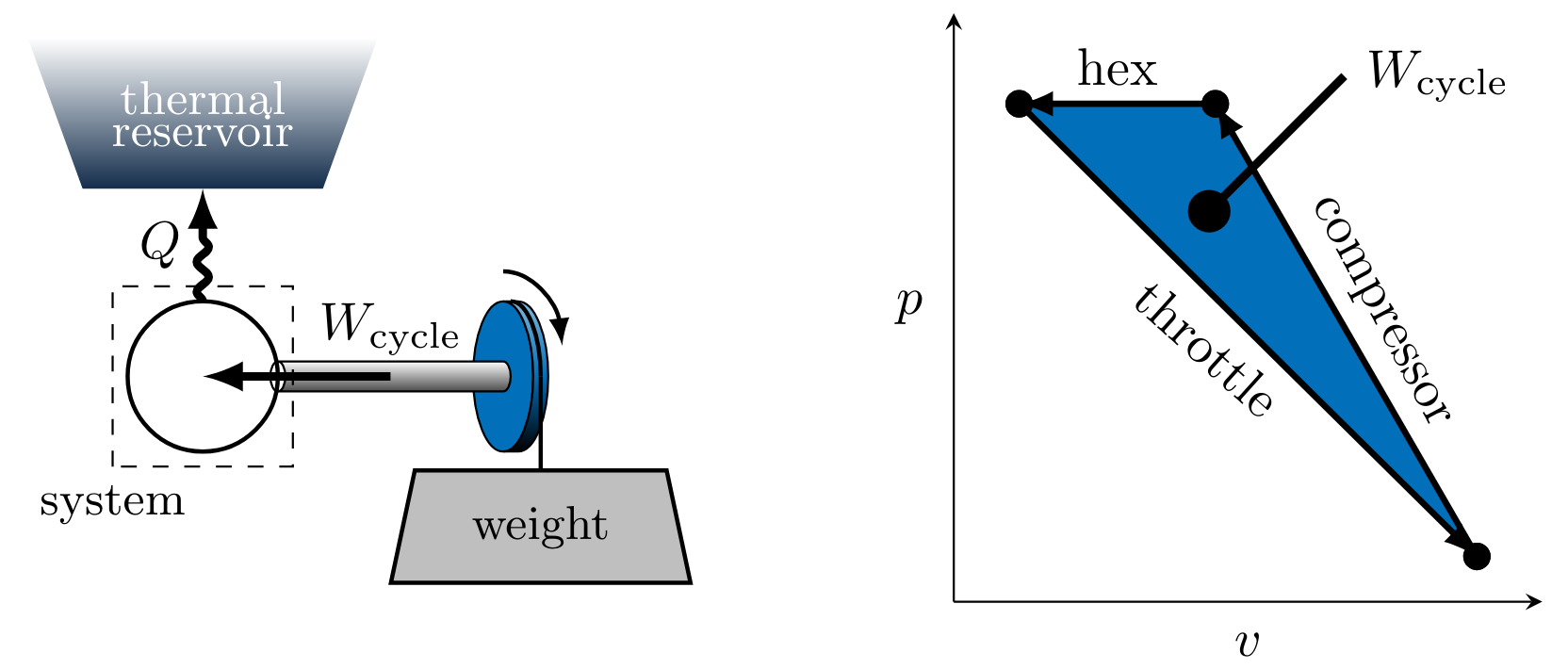
    Work can also be done via shaft work. This can be explained by a shaft, on which a weight and pulley are mounted, providing a mechanism for inputting or extracting work as in Figure 6. Work \( W_{\text{cycle}} \) is done by the lowering mass on the system when the mass is released from its the raised position. The motion of the molecules in the system increases due to the shaft work input. This additional molecular energy temporarily increases the temperature of the system before the excess thermal energy is transmitted as heat \( Q \) to the reservoir.

    Figure 5: Spontaneous lowering of a weight on a pulley.
    Figure 6: A cycle in contact with a single thermal reservoir (left) may operate such that work input leads to an equal amount of heat output. The \(pv\) diagram for one such cycle (right) is shown for a compressor, heat exhanger (hex), and throttle running at steady state.