Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Work and Energy

    Energy

    Potential Energy

    Force and potential energy. #ren-efp
    $$ \begin{aligned}\vec{F} &= -\nabla V \\& = -\frac{\partial V}{\partial x}\hat{\imath} -\frac{\partial V}{\partial y}\hat{\jmath} - \frac{\partial V}{\partial z}\hat{k}\end{aligned} $$

    Beginning with #ren-ec and generalizing it to one-dimensional displacement in the y-direction, the equation becomes:

    $$ \begin{aligned} W &= \vec{F} \cdot \Delta{\vec{y}} \end{aligned} $$

    Assuming the only force applied is the force \( \vec{F} \) , then the system gains potential energy, so the amount of work done is equal to \( \Delta{V} \) .

    $$ \begin{aligned} \Delta{V} &= \vec{F} \cdot \Delta{\vec{y}} \end{aligned} $$

    Rearranging:

    $$ \begin{aligned} F &= \frac{\Delta{V}}{\Delta{y}} \end{aligned} $$

    Since we are interested in the force the field exerts on the system, due to Newton's Third Law, the force is equal and opposite. Therefore, the above result becomes:

    $$ \begin{aligned} F &= -\frac{\Delta{V}}{\Delta{y}} \end{aligned} $$

    If the change in potential energy and displacement is infinitesimally small, this becomes a derivative:

    $$ \begin{aligned} F &= -\frac{dV}{dy} \end{aligned} $$

    Generalizing this result to 3 dimensions, we use the gradient to obtain the following result:

    $$ \begin{aligned} \vec{F} &= -\nabla V \\ & = -\frac{\partial V}{\partial x}\hat{\imath} -\frac{\partial V}{\partial y}\hat{\jmath} - \frac{\partial V}{\partial z}\hat{k} \end{aligned} $$

    Example Problem: Gravitational potential energy. #ren-xgp

    Consider an object of mass \(m\) in the air under the influence of gravity. Derive the potential energy \(V_g\) of the object.

    Using #ren-efp, we can derive the gravitational potential energy. The force due to gravity is:

    $$ \begin{aligned} \vec{F} &= -mg\hat{\jmath} \end{aligned} $$

    Since gravity only acts in one direction, we can simplify #ren-efp to:

    $$ \begin{aligned} F &= -\frac{dV}{dy} \\ -mg &= -\frac{dV}{dy} \\ mg \, dy &= dV \\ \end{aligned} $$

    Integrating both sides:

    $$ \begin{aligned} \int_{V_1}^{V_2} dU &= \int_{y_1}^{y_2} mg \, dy \\ \Delta V & = mg\Delta y \end{aligned} $$

    We can simplify the result by assuming \(U_1\) is zero, and \(y_1\) is at the reference zero-potential height. Therefore, the above becomes:

    $$ \begin{aligned} V_g & = mgy = mgh \end{aligned} $$

    The above result also proves that gravity is a conservative force, as it only depends on the initial and final position of the object.

    Example Problem: Potential energy in a spring. #ren-xsp

    Consider an object of mass \(m\) attached to a spring of stiffness \(k\). Derive the potential energy \(V_s\) stored in the spring.

    Using #ren-efp, we can derive the potential energy in a spring. From the above diagram, the spring force is:

    $$ \begin{aligned} \vec{F} &= -kx\hat{\imath} \end{aligned} $$

    Since the restoring force in a spring only acts in one direction, we can simplify #ren-efp to:

    $$ \begin{aligned} F &= -\frac{dV}{dx} \\ -kx &= -\frac{dV}{dx} \\ kx \, dx &= dV \\ \end{aligned} $$

    Integrating both sides:

    $$ \begin{aligned} \int_{V_1}^{V_2} dU &= \int_{x_1}^{x_2} kx \, dx \\ \Delta V & = \frac{1}{2}k\Delta x^2 = \frac{1}{2}k(x^2_2 - x^2_1) \end{aligned} $$

    We can simplify the result by assuming \(U_1\) is zero, and \(x_1\) is at the reference zero-potential displacement. Therefore, the above becomes:

    $$ \begin{aligned} V & = \frac{1}{2}kx^2 \end{aligned} $$

    The above result also proves that the restoring force in a spring is a conservative force, as it only depends on the initial and final position of the object.

    Warning: Work and energy are not vectors. #wrng-vec

    Work and energy are scalar quantities, as seen by the dot product that results in a scalar value. Positive and negative work/energy values represent either a gain or loss in energy in the system. For instance, in thermodynamics, work done by the system is negative, and work done on the system is positive. In mechanics, positive work represents an object speeding up (putting energy into the system), and negative work represents an object slowing down (taking energy away from the system).

    Gravitational potential energy with uniform gravitational acceleration \(g\). #ren-eg
    $$ V_g = mgh_C $$

    The distance \(h_C\) is the height of the center of mass of the body above the reference height.

    Potential energy stored in a spring with stiffness \(k\). #ren-es
    $$ V_s = \frac{1}{2}kx_C^2 $$

    The distance \(h_C\) is the height of the center of mass of the body above the reference height.

    Work-potential energy theorem. #ren-ewp
    $$ W = -\Delta V $$

    Beginning with the work definition:

    $$ \begin{aligned} W = \vec{F} \cdot \Delta \vec{r} \end{aligned} $$

    Assuming one-dimensional motion, and using the force-potential energy relationship:

    $$ \begin{aligned} W & = -\frac{\Delta V}{\Delta x}\Delta x\\ & = -\Delta V \end{aligned} $$

    Kinetic Energy

    Kinetic energy of a point mass. #ren-ek
    $$ T = \frac{1}{2}mv^2 $$

    We begin with Newton's 2nd Law assuming \( \vec{F} \) is the total external force applied:

    $$ \begin{aligned} \vec{F} &= m\vec{a} \\ & = m\frac{d\vec{v}}{dt} \end{aligned} $$

    Using #ren-efp to relate force and energy:

    $$ \begin{aligned} \frac{dU(\vec{r})}{d\vec{r}} & = m\frac{d\vec{v}}{dt} \end{aligned} $$

    Note that the negative is not found here, as we're interested in the force exerted on the field, not by the field (see derivation in #ren-efp).

    Rearranging then yields:

    $$ \begin{aligned} dU & = m\frac{d\vec{v}}{dt} d\vec{r} \end{aligned} $$

    We can then do the following:

    $$ \begin{aligned} dU & = m\frac{d\vec{r}}{dt} d\vec{v} \\ & = m\vec{v} \, d\vec{v} \\ \end{aligned} $$

    Integrating both sides:

    $$ \begin{aligned} \int_{U_1}^{U_2} dU & = \int_{\vec{v_1}}^{\vec{v_2}}m\vec{v} \, d\vec{v} \\ \Delta U & = \frac{1}{2}m\left[\vec{v} \cdot \vec{v}\right]_{\vec{v_1}}^{\vec{v_2}} \\ \end{aligned} $$

    Assuming an initial velocity of zero, and zero potential energy (i.e the object is at the reference height):

    $$ \begin{aligned} U & = \frac{1}{2}m\left(\vec{v} \cdot \vec{v}\right) \end{aligned} $$

    Using conservation of energy, and the fact that a vector dotted with itself equals its magnitude squared (see #rvi-eg), then:

    $$ \begin{aligned} T & = \frac{1}{2}mv^2\\ \end{aligned} $$

    Another perhaps less intuitive way is to begin with the work definition #ren-ef:

    $$ \begin{aligned} W &= \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d\vec{r} \\ & = \int_{t_1}^{t_2} \vec{F} \cdot \dot{\vec{r}}dt \\ & = \int_{t_1}^{t_2} \vec{F} \cdot \vec{v} \, dt \end{aligned} $$

    Using Newton's 2nd Law assuming \( \vec{F} \) is the total external force applied:

    $$ \begin{aligned} W & = \int_{t_1}^{t_2} m\vec{a} \cdot \vec{v} \, dt \end{aligned} $$

    Note that this integrand looks similar to the following:

    $$ \begin{aligned} \frac{d}{dt}(\vec{u} \cdot \vec{u}) = \dot{\vec{u}} \cdot \vec{u} + \vec{u} \cdot \dot{\vec{u}} = 2\vec{u} \cdot \dot{\vec{u}} \end{aligned} $$

    By the fundamental theorem of calculus, this must mean that:

    $$ \begin{aligned} W = \frac{1}{2}m\left(\vec{v} \cdot \vec{v}\right) \end{aligned} $$

    And we've arrived at the last step of the previous derivation.

    Kinetic energy of an arbitrary body. #ren-ekb
    $$ T = \iiint_{\mathcal{B}} \frac{1}{2} \rho v^2 \, dV $$
    Kinetic energy of a rigid body about the center of mass \(C\). #ren-ekr
    $$ T = \frac{1}{2} m v_C^2 + \frac{1}{2} I_{C,\hat\omega} \omega^2 $$

    Using #ren-ea below, in the case that the point \(Q\) is the center of mass \(C\) we see that \( \vec{r}_{QC} = \vec{r}_{CC} = 0 \) and so the middle term in #ren-ea is eliminated, leaving the result.

    Kinetic energy of a rigid body about the instantaneous center \(M\). #ren-em
    $$ T = \frac{1}{2} I_{M,\hat\omega} \omega^2 $$

    Using #ren-ea below, in the case that the point \(Q\) is the instantaneous center \(M\) we have that \( \vec{v}_Q = \vec{v}_M = 0 \) and so the first two terms are eliminated.

    Kinetic energy of a rigid body about an arbitrary body point \(Q\). #ren-ea
    $$ T = \frac{1}{2} m v_Q^2 + m \vec{v}_Q \cdot \left( \vec\omega \times \vec{r}_{QC} \right) + \frac{1}{2} I_{Q,\hat\omega} \omega^2 $$

    We start with the general expression #rem-eb:

    $$ \begin{aligned} T &= \iiint_{\mathcal{B}} \frac{1}{2} \rho v_P^2 \, dV, \end{aligned} $$
    where we integrate over the body with a location \(P\). We choose a point \(Q\) fixed to the body and use #rkg-er to express the velocity of \(P\) in terms of \( \vec{v}_Q \) and \(\vec\omega\), giving
    $$ \begin{aligned} T &= \iiint_{\mathcal{B}} \frac{1}{2} \rho \|\vec{v}_Q + \vec\omega \times \vec{r}_{QP}\|^2 \, dV \\ &= \iiint_{\mathcal{B}} \frac{1}{2} \rho \left(\vec{v}_Q + \vec\omega \times \vec{r}_{QP}\right) \cdot \left(\vec{v}_Q + \vec\omega \times \vec{r}_{QP}\right) \, dV \\ &= \iiint_{\mathcal{B}} \frac{1}{2} \rho \left( \vec{v}_Q \cdot \vec{v}_Q + 2 \vec{v}_Q \cdot (\vec\omega \times \vec{r}_{QP}) + (\vec\omega \times \vec{r}_{QP}) \cdot (\vec\omega \times \vec{r}_{QP}) \right) \, dV. \end{aligned} $$
    We next use the fact that \( \vec{v}_Q \) and \(\vec\omega\) do not depend on the integration point within the body to pull them outside of the integrals, which results in
    $$ \begin{aligned} T &= \frac{1}{2} \|\vec{v}_Q\|^2 \iiint_{\mathcal{B}} \rho \, dV + \vec{v}_Q \cdot \bigg( \vec\omega \times \iiint_{\mathcal{B}} \rho \vec{r}_{QP} \, dV \bigg) + \iiint_{\mathcal{B}} \frac{1}{2} \rho (\vec\omega \times \vec{r}_{QP}) \cdot (\vec\omega \times \vec{r}_{QP}) \, dV \\ &= \frac{1}{2} m v_Q^2 + \vec{v}_Q \cdot \left( \vec\omega \times m \vec{r}_{QC} \right) + \iiint_{\mathcal{B}} \frac{1}{2} \rho \| \vec\omega \times \vec{r}_{QP} \|^2 \, dV \\ &= \frac{1}{2} m v_Q^2 + m \vec{v}_Q \cdot \left( \vec\omega \times \vec{r}_{QC} \right) + \iiint_{\mathcal{B}} \frac{1}{2} \rho \omega^2 r_{QP}^2 \sin^2\theta \, dV \\ &= \frac{1}{2} m v_Q^2 + m \vec{v}_Q \cdot \left( \vec\omega \times \vec{r}_{QC} \right) + \frac{1}{2} \omega^2 \iiint_{\mathcal{B}} \rho (r_{QP} \sin\theta)^2 \, dV, \end{aligned} $$
    where $\theta$ is the angle between \(\vec\omega\) and \( \vec{r}_{QP} \). But \( r_{QP}\sin\theta \) is simply the orthogonal distance to point \(P\) from the line through \(Q\) in direction \( \vec\omega \) , so from #rem-ei we see that the final integral above is the moment of inertia \( I_{Q,\hat\omega} \) about the axis through point \(Q\).

    Work-kinetic energy theorem. #ren-wk
    $$ W = \Delta T $$

    Skipping the derivation shown in #ren-ep, taking the last step with the integral:

    $$ \begin{aligned} \int dW & = \int_{\vec{v_1}}^{\vec{v_2}}m\vec{v} \, d\vec{v} \\ W & = \frac{1}{2}m\left[\vec{v} \cdot \vec{v}\right]_{\vec{v_1}}^{\vec{v_2}} \\ & = \Delta T \end{aligned} $$

    Work-energy theorem. #ren-eco
    $$ W = Delta T + Delta V $$

    where \(W\) is the work done by non-conservative forces. If non-conservative forces are not present, then it becomes conservation of energy.

    Summary

    Total energy

    $$ \begin{aligned} E &= T + V \\ Total \ Energy &= Kinetic + Potential \end{aligned} $$

    Kinetic

    Point Mass. #sum-pm
    $$ T = \frac{1}{2} m v^2 $$
    Rigid Body. #sum-rb
    $$ \begin{aligned} T &= \frac{1}{2} m \ {v_c}^2 + \frac{1}{2} I_c \ \omega^2 \quad \text{(about center of mass C)} \\ T &= \frac{1}{2} \ I_O \ \omega^2 \quad \text{(if point O is pinned)} \\ T &= \frac{1}{2} \ I_M \ \omega^2 \quad \text{(if M is the instantaneous center)} \end{aligned} $$

    Potential

    Gravitational. #sum-pg
    $$ V = m \ g \ h_c \quad \text{ (h is the height of center of mass)} $$
    Elastic. #sum-pe
    $$ V = \frac{1}{2}\ k \ x^2 \quad \text{ (k is the spring stifness and x is elongation)} $$

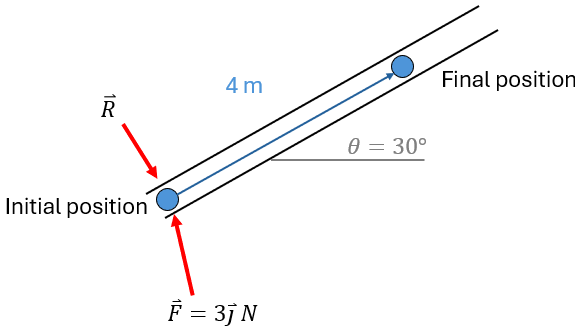
    Work

    Work-Energy Principal #wan-we
    $$ W = \Delta{E} = E_f - E_0 $$

    Work done by a Force

    Work done by a force \(\vec{F}\). #ren-wf
    $$ \begin{aligned}W &= \int_{\vec{r}_1}^{\vec{r}_2} \vec{F} \cdot d\vec{r} \\& = \int_{t_1}^{t_2} \vec{F} \cdot \dot{\vec{r}}dt\end{aligned} $$
    Work done by a constant force \(\vec{F}\). #ren-wc
    $$ W = \vec{F} \cdot \Delta \vec{r} $$

    The change in position is \( \Delta \vec{r} = \vec{r}_2 - \vec{r}_1 \) .

    Work done by a constraint force \(\vec{F}\). #ren-wt
    $$ W = 0 $$

    The work \(W\) is by a force of constraint force \( \vec{F} \) .

    By definition a constraint force \( \vec{F} \) does not permit movement in the direction that it applies. This means that the constraint force and the displacement are always orthogonal and the dot product between orthogonal vectors is zero.

    Work done by a moment \(M\). #ren-wm
    $$ \begin{aligned}W &= \int_{\theta_1}^{\theta_2} M \, d\theta \\& = \int_{t_1}^{t_2} M \dot\theta \, dt \\&= M \, \Delta \theta \text{ (for constant M)}\end{aligned} $$

    The rotation angle \(\theta\) is measured around the same axis \( \vec{a} \) about which the moment \(M\) is applied.

    Example Problem: Constant Force. #wfe-cf

    Work done by \( \vec{F} \) is \( W = 6 J \). Assume no gravity, frictionless, constraint force \( \vec{R} \) of the slot of the mass.

    What is the increase in energy of the mass?

    1. \( > 6 J \)
    2. \( 6 J \)
    3. \( < 6 J \)
    4. Need to first find \( \vec{R} \)

    B. \( 6 J \)

    $$ \Delta E = W = \vec{R} \ \cdot \Delta \ \vec{r} \quad , \quad \vec{R} \perp \vec{r} $$

    Conservative vs Non-conservative forces

    A conservative force is one such that the work done by the force only depends on the initial and final positions of the object (i.e independent of the path taken by the object). Examples of conservative forces are gravity and spring force, where only the initial and final displacements are needed to calculate the work done by those forces. Examples of a non-conservative force are any type of drag forces (e.g friction, air resistance).

    The diagram below illustrates different paths and the work done by a conservative forces vs. a non-conservative force.

    If the force moving an object from point \(A\) to point \(B\) was conservative, the work done by that force in all paths is equal. If the force was non-conservative, the work done by that force is not equal, and it depends on the path length.

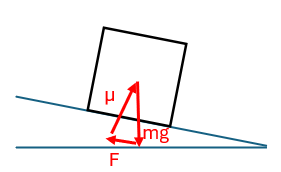
    Work done by Friction

    $$ W = \Delta{E} = E_f - E_i $$

    Work done by friction can be positive, zero, or negative.

    Example Problem: Friction during rolling wihtout slip. #wdf-rws
    1. Which direction does friction force \( \vec{F} \) act?
      1. Right
      2. Zero
      3. Left
    2. What is the work done by friction?
      1. \( > 0 \)
      2. Zero
      3. \( < 0 \)
    1. A.
    2. B.
      $$ W = \int \vec{F} \cdot \vec{r} \,dt = 0 \quad \text{as} \quad \vec{r} = 0 $$
      • Friction prevents slip
      • Converts rotation motion into translational

    Work done by a Moment

    $$ W = \int_{\theta_0}^{\theta_f} M_z \,d\theta = \int_{t_0}^{t_f} M_z \ \dot{\theta} \,d\theta $$
    Example Problem: Rod with friction moment. #wdm-rm

    Rod shown above starts from rest, falls to horizontal, friction moment of 2 Nm. What is the work done by friction?

    1. \( \geq 2 J \)
    2. \( 0 < W < 2 J \)
    3. \( = 0 \)
    4. \( W \leq -2 J \)

    D.

    \( W = \int_{\frac{\pi}{4}}^0 (2 Nm) \, d\theta \\ = \mu \ (\Delta \theta) \\ = (2 Nm)(0- \frac{\pi}{4}) = -\frac{\pi}{2} J \)

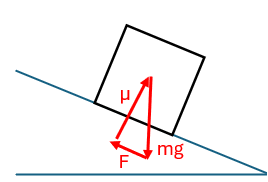
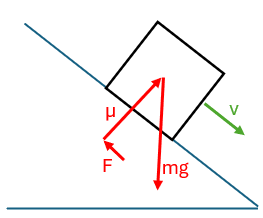
    Friction

    Stick Transition Slip
    • No relative motion \( v_{px} = 0 \) and \( a_{px} = 0 \)
    • \( F \leq \mu N \)
    • No relative motion \( v_{px} = 0 \) and \( a_{px} = 0 \)
    • Critical friction force \( F = \mu N \)
    • Relative motion \( v_{px} \neq 0 \) or \( a_{px} \neq 0 \)
    • \( F = \mu N \)
    • \( \hat{F} \) opposed motion

    Solution procedure

    Known Case

    1. Determine case: stick, transition, slip (and direction)
    2. FBD, equations of motion (or statics), solve

    Unknown Case

    1. Try stick
      1. Assume \( v_{px} = 0 \) and \( a_{px} = 0 \)
      2. Solve for N, F
      3. Check \( |F| \leq \mu |N| \)
    2. Try slip
      1. Assume \( F = \mu N \) (in one direction)
      2. Solve for motion of contact point and N, F
      3. Check \( v_{px} \neq 0 \) or \( a_{px} \neq 0 \) and \( \hat{F} \) opposed motion (\( \hat{v} \) or \( \hat{a} \))
    3. Otherwise
      1. Assume \( F = \mu N \) (in opposite direction) and resume from step B.2

    Momentum

    Momentum is one of the most fundamental concepts in dynamical systems. It is often convenient to derive equations of motion using momentum. Furthermore, it is related to kinetic energy and Newton's second law. Conservation of momentum is one of the three conservation laws in dynamics alongside conservation of energy and mass.

    Linear momentum of a rigid body. #rec-lm
    $$ \vec{p} = m\vec{v}_C $$

    Unlike energy, momentum is a vector, and its direction is the same as the direction of the velocity of the center of mass.

    Furthermore, angular momentum is analogous to linear momentum. The angular momentum of a rigid body is shown below.

    Angular momentum of a rigid body rotating about principal axis \(\hat{a}\) through point \(O\). #rec-am
    $$ \vec{L}_O = I_{O,\, \hat{a}} \vec{\omega} $$

    Momentum is also closely linked to force and moments. More specifically, the change in momentum and Newton's second law can be related.

    Newton's equations and linear momentum. #rec-mn
    $$ \begin{aligned}\vec{F} &= \frac{d\vec{p}_C}{dt}\\&= \dot{\vec{p}_C}\end{aligned} $$

    We begin with Newton's second law:

    $$ \begin{aligned} \vec{F} &= m\vec{a}_C\\ &= m \frac{d\vec{v}_C}{dt} \\ \end{aligned} $$

    Assuming constant mass, then this can be rewritten as:

    $$ \begin{aligned} \vec{F} &= \frac{d}{dt} (m\vec{v}_C)\\ & = \frac{d\vec{p}_C}{dt} \\ & = \dot{\vec{p}_C} \end{aligned} $$

    Warning: \(\vec{F} = \dot{\vec{p}_C}\) is not applicable with variable mass. #rec-wm

    In the derivation of #ren-mn, the mass was assumed to be constant. In the case of a rocket expelling propellant, this does not work. See the rocket equation derivation further down.

    As aforementioned, angular momentum is analogous to linear momentum, so the above equation can also be derived using moments and angular momentum.

    Newton's equations and angular momentum. #rec-mm
    $$ \begin{aligned} \vec{M}_{C} &= \frac{d\vec{L}_C}{dt}\\&= \dot{\vec{L}_C}\end{aligned} $$

    We begin with Newton's second law:

    $$ \begin{aligned} \vec{M}_{C} &= I_{C, \hat{a}}\vec{\alpha}\\ &= I_{C, \hat{a}} \frac{d\vec{\omega}}{dt} \\ \end{aligned} $$

    Assuming constant moment of inertia, then this can be rewritten as:

    $$ \begin{aligned} \vec{M}_{C} &= \frac{d}{dt} (I_{C, \hat{a}}\vec{\omega})\\ & = \frac{d\vec{L}_C}{dt} \\ & = \dot{\vec{L}_C} \end{aligned} $$

    From the above equations, it is clear to see that linear momentum is conserved if and only if the sum of external forces acting on the system is zero, and angular momentum is conserved if and only if the sum of external moments acting on the system is zero.

    Conservation of linear momentum. #rec-lmc
    $$ \begin{aligned} \vec{F} &= \frac{d\vec{p}_C}{dt}\\&= \vec{0}\end{aligned} $$
    Warning: Linear momentum is conserved if and only if the sum of external forces is zero #rec-wlmc

    As seen from #rec-lmc, linear momentum is conserved if the sum of the external forces is zero. This is why choosing an appropriate system and drawing a free-body diagram is crucial in determining whether linear momentum is conserved. See examples below.

    Conservation of angular momentum. #rec-amc
    $$ \begin{aligned} \vec{M}_{C} &= \frac{d\vec{L}_C}{dt}\\&= \vec{0}\end{aligned} $$
    Warning: Angular momentum is conserved if and only if the sum of external moments is zero. #rec-wamc

    As seen from #rec-amc, angular momentum is conserved if the sum of the external moments is zero. This is why choosing an appropriate system and and drawing a free-body diagram is crucial in determining whether angular momentum is conserved. See examples below.

    Example Problem: An object in free-fall. #rec-xlmc

    An object is free-falling in the air under the influence of gravity. Take the system to be the object. Is linear momentum conserved?

    Begin with a free-body diagram of the forces acting on the system:

    Write Newton's second law in terms of momentum:

    $$ \begin{aligned} \vec{F} &= \frac{d\vec{p}_C}{dt} \\ m\vec{g} & = \frac{d\vec{p}_C}{dt} \end{aligned} $$

    Verifying with conservation of linear momentum, it's clear to see that the sum of external forces is not zero, as the weight of the object is external to the system, and is not balanced by any other force. Therefore, linear momentum is not conserved.

    If however, the system was chosen to be the object and the Earth, then linear momentum is conserved, as by Newton's third law, the Earth exerts a force equal to \(mg\), and the object exerts a force \(-mg\) on the Earth. Therefore, the sum of external forces acting on the system is zero, and linear momentum is conserved.

    Example Problem: A satellite in a circular orbit around the Earth. #rec-xamc

    A satellite of mass \(m\) is inserted into a circular orbit around the Earth. Take the system to be the satellite and the Earth. Ignoring the effects of gravity from any other celestial body, is angular momentum conserved?

    Begin with a free-body diagram of the forces acting on the system. Assume the altitude of the satellite is negligble enough so that the gravitational acceleration is $g$. Otherwise, Newton's Law of Gravitation would need to be used to denote the forces.

    Write Newton's second law in terms of momentum:

    $$ \begin{aligned} \vec{M}_C &= \frac{d\vec{L}}{dt} \\ \vec{r} \times m\vec{g} - \vec{r} \times m\vec{g} & = \frac{d\vec{L}}{dt} \end{aligned} $$

    Verifying with conservation of angular momentum, it's clear to see that the sum of external moments is zero, as the moment due to the pull of the Earth on the satellite is equal and opposite to the moment due to the pull of the satellite on the Earth. Moreover, those moments are equal to zero as the position vector $r$ and $mg$ are parallel, which yields a cross product of zero.

    Interestingly, angular momentum is also related to linear momentum if the object is a point mass.

    Angular momentum of a point mass \(P\) about a stationary point \(O\). #rec-al
    $$ \vec{L}_{O} = \vec{r}_{OP} \times \vec{p}_P $$

    Begin with the relationship between angular momentum and moment at #rec-mm

    $$ \begin{aligned} \vec{M}_C &= \frac{d\vec{L}}{dt}\\ \end{aligned} $$

    For simplicity's sake, assume there's only one external moment due to a force applied at point \(P\). Recall the definition of moment due to a force applied at point \(P\):

    $$ \begin{aligned} \vec{M}_O &= \vec{r}_{OP} \times \vec{F}_P \\ \end{aligned} $$

    Then #rec-mm becomes:

    $$ \begin{aligned} \frac{d\vec{L}}{dt} &= \vec{r}_{OP} \times \vec{F}_P \end{aligned} $$

    Using the relationship between linear momentum and force at #rec-mn , the above equation becomes:

    $$ \begin{aligned} \frac{d\vec{L}}{dt} &= \vec{r}_{OP} \times \vec{F}_P \\ & = \vec{r}_{OP} \times \frac{d\vec{p}_P}{dt} \end{aligned} $$

    Multiplying both sides by $dt$ yields:

    $$ d\vec{L} = \vec{r}_{OP} \times d\vec{p}_P $$

    Recall integration by parts:

    $$ \int u \, dw = uw - \int w \, du $$

    Setting \( dw = d\vec{p}_P and u = \vec{r}_{OP} \) , then:

    $$ \begin{aligned} u = \vec{r}_{OP} \quad \quad \quad du = \vec{v}_P \,dt \\ w = \vec{p}_P \quad \quad \quad dw = d\vec{p}_P \end{aligned} $$

    Therefore:

    $$ \begin{aligned} \int d\vec{L} &= \int \vec{r}_{OP} \times d\vec{p}_P \\ &= \vec{r}_{OP} \times \vec{p}_P - \int \vec{p}_P \times \vec{v}_P \,dt \end{aligned} $$

    However, \( \vec{p}_P = m\vec{v}_P \) as established in #rec-lm:

    $$ \begin{aligned} \vec{L} &= \vec{r}_{OP} \times \vec{p}_P - \int m\vec{v}_P \times \vec{v}_P \,dt \end{aligned} $$

    The cross product of a vector with itself is zero (cross product self-annihilation). So the integral of \( \int m\vec{v}_P \times \vec{v}_P \, dt \) is a constant, which is the initial angular momentum. Assuming this is zero, we arrive at the desired expression.

    Impulse

    Impulse is a quantity that describes the effect of a resultant force acting over time. Naturally, impulse is related to momentum.

    Impulse. #rec-ij
    $$ \vec{J} = \int_{t_1}^{t_2} \vec{F} \, dt $$

    Note that impulse, like momentum, is a vector. Its direction is the same direction as the net force.

    As seen from the equation above, this naturally leads to relating the impulse and momentum. Specifically, impulse is the change in momentum.

    Impulse-momentum theorem. #rec-jm
    $$ \vec{J} = \Delta \vec{p}_C $$

    From Newton's second law and linear momentum at #rec-mn:

    $$ \vec{F} = \frac{d\vec{p}_C}{dt} $$

    Plugging into the impulse definition:

    $$ \begin{aligned}\vec{J} &= \int_{t_1}^{t_2} \frac{d\vec{p}_C}{dt} \, dt \\&= \int_{\vec{p}_1}^{\vec{p}_2} d\vec{p} \\&= \vec{p}_2 - \vec{p}_1 = \Delta \vec{p}_C\end{aligned} $$

    Example: The Rocket Equation #rec-xr

    As stated in the warning at #rec-wm, the relationship between Newton's equations and linear momentum are not applicable for a system whose mass is changing with time. To use that relationship, a few things must be changed. Consider the figure below of a rocket.

    The vector \( \vec{v} \) is the velocity of the center of mass of the rocket relative to an inertially fixed point in space, \(O\). The vector \( \vec{c} \) is the effective exhaust velocity. It is the average equivalent velocity at which propellant is ejected from the rocket relative to the rocket. We will explain further how it relates to what is often a characteristic value of the performance of an engine, called the specific impulse, denoted by \( I_{sp} \).

    Since the rocket is ejecting propellant, the rate at which this propellant is expelled is the mass flow rate, denoted by \( \dot{m} \). In this case, it will be \( -\dot{m} \) as the rocket is expelling propellant. To derive the rocket equation, we will need to calculuate the momentum at time \(t\), and at time \(t + dt\), a little time after expelling propellant.

    The momentum at time \(t\) is simply \( \vec{p}_1 = m\vec{v} \). The momentum at time \(t + dt\) consists of two parts: the momentum of the rocket without the mass lost to propellant expulsion, and the momentum of the propellant leaving the rocket. First, the momentum of the rocket at time \(t + dt\) is given by:

    $$ \begin{aligned}\vec{p}_{2, rocket} = (m + \dot{m}dt)(\vec{v} + d\vec{v})\end{aligned} $$

    You can expand the result to make sure it makes sense:

    $$ \begin{aligned}\vec{p}_{2, rocket} &= (m + \dot{m}dt)(\vec{v} + d\vec{v}) \\& = m\vec{v} + md\vec{v} + \dot{m}\vec{v}dt + \dot{m}d\vec{v}dt\end{aligned} $$

    The expression \( m\vec{v} \) is the initial momentum of the rocket. The expression \( md\vec{v} \) is the momentum of the rocket due to the velocity change. The expression \( \dot{m}\vec{v}dt \) is the momentum of the propellant at the initial velocity. (Note that \( \dot{m}dt \) is the mass of the propellant since \( \dot{m} = -\frac{dm}{dt} \)). The expredssion \( \dot{m}d\vec{c}dt \) is the momentum of the propellant due to the velocity change.

    The second part of the momentum is the momentum of the propellant leaving the rocket. This expression is a little tricky, as the effective exhaust velocity is relative to the rocket as aforementioned, so we need to obtain the effective exhaust velocity \( \vec{c} \) relative to the inertially fixed point, \(O\). Otherwise, Newton's equations cannot work. The exhaust velocity relative to \(O\) is:

    $$ \vec{c}_{O} = \vec{c}_{rocket} + \vec{v}_{rocket, O} = \vec{c} + \vec{v} $$

    Then the momentum of the propellant being exhausted:

    $$ \vec{p}_{2, p} = -\dot{m}dt(\vec{c} + \vec{v}) $$

    So the total momentum at time \(t + dt\):

    $$ \vec{p}_2 = (m + \dot{m}dt)(\vec{v} + d\vec{v}) - \dot{m}dt(\vec{c} + \vec{v}) $$

    By the impulse-momentum theorem:

    $$ \begin{aligned}\vec{J} = \Delta \vec{p}_C = \vec{F} dt\end{aligned} $$

    Plugging into the above equation:

    $$ \begin{aligned}(m + \dot{m}dt)(\vec{v} + d\vec{v}) - \dot{m}dt(\vec{c} + \vec{v}) - m\vec{v} = \vec{F} dt\end{aligned} $$

    Expanding:

    $$ \begin{aligned}m\vec{v} + md\vec{v} + \dot{m}\vec{v}dt + \dot{m}d\vec{v}dt - \dot{m}\vec{c}dt - \dot{m}\vec{v}dt - m\vec{v} = \vec{F} dt\end{aligned} $$

    Simplifying:

    $$ \begin{aligned}md\vec{v} + \dot{m}d\vec{v}dt - \dot{m}\vec{c}dt &= \vec{F}dt \\md\vec{v} + \dot{m}dt(d\vec{v} - \vec{c}) &= \vec{F}dt\end{aligned} $$

    Dividing by $dt$:

    $$ \begin{aligned}m\frac{d\vec{v}}{dt} + \dot{m}(d\vec{v} - \vec{c}) &= \vec{F} \\m\vec{a} + \dot{m}(d\vec{v} - \vec{c}) &= \vec{F}\end{aligned} $$

    This shows that Newton's equations in linear momentum form do not work with variable mass, as \( \vec{F} - m\vec{a} \) is not zero in this case. Rearranging one more time:

    $$ \begin{aligned}m\frac{d\vec{v}}{dt} = \dot{m}(d\vec{v} - \vec{c}) + \vec{F}\end{aligned} $$

    Note the positive next to \( \dot{m} \) is due to the loss of mass, as aforementioned earlier. The above equation is called the ideal rocket equation, or Tsiolkovsky rocket equation.

    Collisions

    A collision is when two or more objects exert forces on each other in a relatively short time. These problems are usually solved using conservation of momentum and energy. There are two general types of collisions: elastic and inelastic collisions. They are categorized by the state of the kinetic energy before and after the collisions:

    type of collision definition
    elastic collisions collisions where there is no loss in kinetic energy
    inelastic collisions collisions where there are losses in kinetic energy, typically due to internal friction

    Typically in collisions, it is assumed it takes place on a frictionless surface. This is important, since if friction were to be present, the system is not isolated, and therefore momentum is not conserved.

    The types of collisions that will be noted are perfectly inelastic and elastic collisions.

    The steps involved in solving a perfectly elastic collision with conservation of momentum and energy are detailed as follows:

    Solution procedure of perfectly elastic collisions. #rec-ecp
    $$ \begin{aligned} m_1 \vec{v}_{1, i} + m_2 \vec{v}_{2, i} &= m_1 \vec{v}_{1, f} + m_2 \vec{v}_{2, f} \\ \frac{1}{2} m_1 v_{1, i}^2 + \frac{1}{2} m_2 v_{2, i}^2 & = \frac{1}{2} m_1 v_{1, f}^2 + \frac{1}{2} m_2 v_{2, f}^2 \end{aligned} $$

    where subscripts \(i, f\) denote initial and final velocities, respectively.

    Below an animation to simulate a 1D perfectly elastic collision between two blocks.

    \(m_1\)

    \(v_1\)

    \(m_2\)

    \(v_2\)

    The solution procedure to solve a perfectly inelastic collisions is simpler, as the objects stick together after an inelastic collision. It involves using conservation of momentum only, as kinetic energy is lost in the collision, as aforementioned.

    Solution procedure of perfectly inelastic collisions. #rec-icp
    $$ m_1 \vec{v}_{1, i} + m_2 \vec{v}_{2, i} = (m_1 + m_2)\vec{v}_f $$

    where subscripts \(i, f\) denote initial and final velocities, respectively.

    Note the \( \vec{v}_f \) shown above is the velocity of the center of mass. It is the same before and after the collision due to conservation of momentum where the net external force is zero (and therefore, the acceleration of the center of mass).

    Below is an animation to simulate a 1D perfectly inelastic collision between two blocks.

    \(m_1\)

    \(v_1\)

    \(m_2\)

    \(v_2\)

    One way collisions can be classified into elastic and inelastic collisions is using what is called the coefficient of restitution. It is the ratio of the final to initial relative speeds between two objects after the collision. It can be a way to solve collisions that are not classified as perfectly inelastic or elastic, as well as collisions of more than two objects.

    Coefficient of restitution. #rec-cor
    $$ e = \frac{\left|v_{2,f} - v_{1,f}\right|}{\left|v_{2,i} - v_{1,i}\right|} $$

    where subscripts \(i, f\) denote initial and final velocities, respectively.

    Using the solution procedure of perfectly elastic collisions at #rec-ecp and assuming a one-dimensional collision:

    $$ \begin{aligned}m_1 v_{1, i} + m_2 v_{2, i} &= m_1 v_{1, f} + m_2 v_{2, f} \\\frac{1}{2} m_1 v_{1, i}^2 + \frac{1}{2} m_2 v_{2, i}^2 & = \frac{1}{2} m_1 v_{1, f}^2 + \frac{1}{2} m_2 v_{2, f}^2\end{aligned} $$

    From conservation of kinetic energy:

    $$ \begin{aligned}m_1 \left(v_{1, i}^2 - v_{1, f}^2\right) &= m_2 \left(v_{2, f}^2 - v_{2, i}^2\right)\end{aligned} $$

    Using the difference of two squares :

    $$ \begin{aligned}m_1 \left(v_{1, i} - v_{1, f}\right) \left(v_{1, i} + v_{1, f}\right) &= m_2 \left(v_{2, f} - v_{2, i}\right) \left(v_{2, f} + v_{2, i}\right)\end{aligned} $$

    From conservation of linear momentum:

    $$ \begin{aligned}m_1 \left(v_{1, i} - v_{1, f}\right) &= m_2 \left(v_{2, f} - v_{2, i}\right)\end{aligned} $$

    Divide the conservation of linear momentum equation:

    $$ \begin{aligned}\frac{m_1 \left(v_{1, i} - v_{1, f}\right)}{m_2 \left(v_{2, f} - v_{2, i}\right)} &= 1\end{aligned} $$

    Divide the conservation of kinetic energy equation:

    $$ \begin{aligned}\frac{m_1 \left(v_{1, i} - v_{1, f}\right)}{m_2 \left(v_{2, f} - v_{2, i}\right)} &= \frac{\left(v_{2, f} + v_{2, i}\right)}{\left(v_{1, i} + v_{1, f}\right)}\end{aligned} $$

    Substituting the division from conservation of momentum into the division from the conservation of kinetic energy:

    $$ \begin{aligned}1 &= \frac{\left(v_{2, f} + v_{2, i}\right)}{\left(v_{1, i} + v_{1, f}\right)}\end{aligned} $$

    Rearranging:

    $$ \begin{aligned}v_{1, i} + v_{1, f} &= v_{2, f} + v_{2, i} \\v_{1, i} - v_{2, i} & = -\left(v_{1, f} - v_{2, f}\right)\end{aligned} $$

    Finally, one more divison and taking the absolute value:

    $$ \begin{aligned}1 & = \frac{\left|v_{2,f} - v_{1,f}\right|}{\left|v_{2,i} - v_{1,i}\right|}\end{aligned} $$

    Which equals 1, which is the coefficient of restitution for a perfectly elastic collision.

    The range of values of the coefficient of restitution corresponds to different types of collisions. It is a dimensionless parameter, usually between 0 and 1. Those ranges are tabulated below.

    range type of collision
    \(e = 0\) This corresponds to a perfectly inelastic collision. The velocity of both objects after the collision is the same
    \(0 < e < 1\) This corresponds to an inelastic collision that happens in the real world, where some kinetic energy is lost
    \(e = 1\) This corresponds to a perfectly elastic collision, where no kinetic energy is lost.
    \(e > 1\) This corresponds to a superelastic collision, where energy is gained/released, like a chemical reaction, a reduction of rotational energy.

    Did you know?

    Counting the number of collisions with two simple objects, such as blocks, billiard balls, can be used to estimate \(\pi\) to any accuracy. Mathematician Gregory Galperin of Eastern Illinois University discovered this in 1995 and published this in 2003. Famous YouTuber 3Blue1Brown made a video on this explaining this seemingly paradoxical result. However, looking at the velocity phase space, which is graphing the velocity of \(m_1\) on one axis, and the velocity of \(m_2\) on another. This arises from conservation of kinetic energy in elastic collisions.

    Did you know?

    There was a time when hitting the perfect shot in a game of billiards could result in the ball to explode. They were made from nitrocellulose, which is a plastic that is easily combustible, as an alternative to ivory. This corresponds to a coefficient of restitution greater than 1.

    Applications