Current page:

Substances

Phases of matter

A phase of matter is homogeneous in both its molecular composition and the structure of its molecules with respect to one another.

Pure Substance:

A pure substance is when a substance occurs in a single phase and is composed of a single type of molecule.

Solid:

A substance that has a definite shape and volume is a solid. The molecules in a solid are tightly packed, and cannot move past one another but vibrate.

Liquid:

A substance that has a definite volume, but no definite shape is a liquid, taking on the shape of their container. The molecules in a liquid are constantly moving yet still in contact with one another.

Gas:

A substance with no definite shape or volume, gases take on the shape or volume of the container they are surrounded by. Molecules can move freely and have negligible intermolecular interactions.

Phase Diagrams

A phase diagram is like a map and predicts the phase of a substance according to its thermodynamic properties: $ p $, $ T $, $ v $, $ u $, and $ h $. An example of a $ pv $ liquid-vapor phase diagram for a pure substance is shown below:

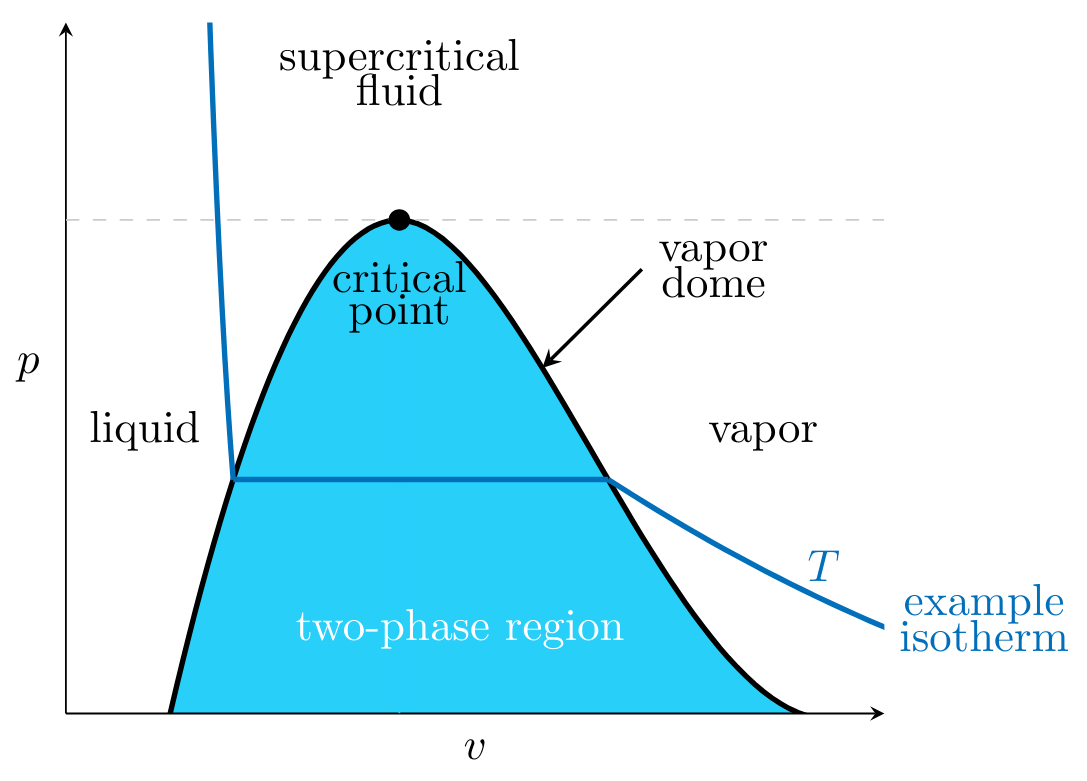
Figure 1: A $pv$ liquid-vapor phase diagram for a pure substance illustrating the critical point, vapor dome, and liquid and vapor regions.

Critical Point:

Point at which at lesser pressures the substance exists as either a liquid or vapor, and above exists as a supercritical fluid.

Vapor Dome:

Region within the dome-like curve known as the two-phase region, where some part of the substance is in a liquid phase, and some part is in a vapor phase. The substance is in a liquid phase when its $ p $ and $ v $ lie in the region to the left of the vapor dome and in a vapor phase when its $ p $ and $ v $ lie in the region to the right of the vapor dome.

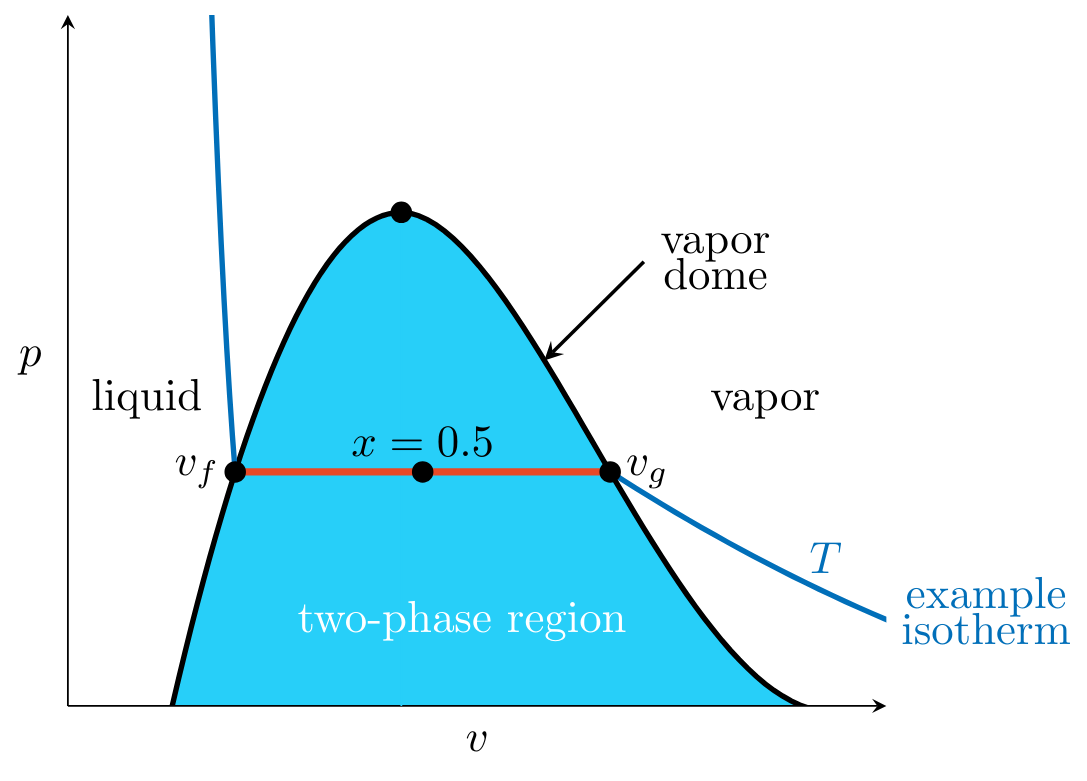
If $ v $ lies at the intersection of the isotherm and the left side of the vapor dome, the system is said to be in the saturated liquid state with specific volume $ v_f $.
If $ v $ lies at the intersection of the isotherm and the right side of the vapor dome, the system is said to be in the saturated vapor state $ v_g $.
If the system is halfway between the liquid and vapor states (see Figure 2) such that the mass of the liquid portion $ m_f $ equals the mass of the vapor portion $ m_g $, then its quality $ x $ is given by

$$ x \equiv \frac{m_g}{m_f + m_g} = 0.5 $$

Figure 2: A $pv$ liquid-vapor phase diagram for a pure substance illustrating thermodynamic properties that define the two-phase region.

Supercritical Fluid:

Phase of the substance when existing above the critical point, and possesses characteristics similar to both liquids and gases, but strictly behaves as neither.

Isotherm:

For a given $ p $ and $ v $, the substance's $ T $ lies on an isotherm. The segment of the isotherm within the vapor dome is horizontal because phase transitions occur at a constant $ T $ and $ p $.

State of a Substance:

If any two independent intensive variables are known ($ T, v, p, x, h, u $), they fix the state of the substance. (Intensive variables are independent of mass. For example, specific volume $ v $ is intensive. Volume $ V=mv $ is not.)

Critical Values and Ideal Gases

Ideal gases are modeled as having internal energy entirely composed of kinetic energy due to the absence of any interactions between the particles of the gas, which occurs when:

The particles are far away from each other, at lower pressure or density
the kinetic energy of the particles is so large as to render the energy due to interactions between them negligible, at high temperature

Reduced Values:

Low and high are relative terms and depend on the particular gas, specifically its phase behavior. Reduced values are normalized with respect to their values at the critical point to describe where gases are far enough away from the vapor dome to behave ideally,

($ p_c $, $ v_c $, and $ T_c $). The following expressions

$$ p_R = p/p_c \qquad T_R = T/T_c \qquad v_R^\prime = \frac{v}{R(T_c/p_c)} $$

define the reduced pressure, reduced temperature, and pseudoreduced specific volume.

Compressibility factor:

The compressibility factor, $ Z $, for an ideal gas equals 1, meaning a gas behaves ideally at infinitely small $ p $. Therefore, the more deviation of Z from unity the less ideally a gas behaves.

Compressibility factor $Z$

$$ Z = \frac{pv}{RT} $$

Ideal Gases

A gas is a state of matter that has neither independent shape nor volume. When contained, the atoms or molecules that comprise it interact with every boundary of the container.

Ideal Gas Assumptions

An ideal gas is a hypothetical model of a gas that follows the assumptions that

molecules are infinitesimally small (just points in space)
- ideal gas molecules never collide with one another
- ideal gas molecules occupy no volume
intermolecular forces are zero
- ideal gas molecules have no potential energies between molecules
- internal energy is only a function of kinetic energy

Figure 3: A sub-volume of gas next to a sub-section of the container wall having area, $A$.

Equation of State

It has been shown empirically that an ideal gas obeys the equation of state

Ideal-gas law

$$ pV=n\overline{R}T $$

$\overline{R}$ in different unit systems

$$ \overline{R} = \begin{cases} &8.314 \textrm{ kJ/kmol}\cdot\textrm{K}\\ &1.986 \textrm{ Btu/lbmol}\cdot\textrm{$^\circ$R}\\ &1545 \textrm{ ft $\cdot$lbf/kmol}\cdot\textrm{$^\circ$R}\\ \end{cases} $$

Temperature Effects

$ \overline{R} $ defines the proportionality constant that converts the average translational kinetic energy of a single particle, $ \langle KE\rangle $, to temperature ($ N_A $ is Avagadro's number)

$\color{red} \textrm{Title?} $

$$ T = \frac{2}{3} \frac{N_A}{\overline{R}}\langle KE \rangle. $$

Internal energy of an ideal gas depends only on the total molecular kinetic energy. Therefore, internal energy is solely a function of the temperature, $ T $, and mass of the gas, $ m $. The rate of change of the specific internal energy, $ u $, where $ u = U/m $, of an ideal gas with respect to $ T $ is its , $ c_v $

Constant volume specific heat $c_v$ in an ideal gas

$$ \frac{du}{dT} = c_v $$

It follows that the change in internal energy of an ideal gas due to a change in temperature from $ T_1 $ to $ T_2 $ is given by

Internal energy-temperature relationship

$$ \Delta U = U_2 - U_1 = m\int_{T_1}^{T_2} c_v dT. $$

Incompressible Fluids

In the incompressible substance model, the volume of a quantity of a substance cannot be compressed or expanded, thus its specific volume is constant.

Internal Energy of Incompressible Fluids

Because the specific volume is not changing, the average intermolecular potential energy, which from the average distance between molecules, cannot change. Thus, the only contribution to an incompressible substance's internal energy comes from atomic and molecular kinetic energy, quantified via temperature. It follows that, like the ideal gas model, the internal energy of an incompressible substance is a function of temperature only and

$$ u = u(T) $$

Constant volume specific heat $c_v$ in an incompressible fluid

$$ \frac{du}{dT} = c_v $$

Specific Heat of Incompressible Fluids

For an incompressible substance, constant pressure specific heat $ c_p $ equals constant volume specific heat $ c_v $. $ c_p $ is defined as the partial derivative of the enthalpy $ h $, while pressure $ p $ is held constant.

Constant pressure specific heat

$$ c_p \equiv \left(\frac{\partial h}{\partial T}\right)_p. $$

By definition $ h = u+pv $, thus at constant $ p $ and for an incompressible substance (constant $ v $), we can write the partial derivative of $ h $ with respect to $ T $ as

$$ \left(\frac{\partial h}{\partial T}\right)_p = \left(\frac{\partial u}{\partial T}\right)_p = \frac{du}{dT} = c_v $$

where the conversion from a partial to total derivative arises because $ u = u(T) $ for an incompressible substance. Therefore $ c_p = \left(\frac{\partial h}{\partial T}\right)_p = c_v $ for an incompressible substance.

$c_v$ & $c_p$ equivalence for incompressible substances

$$ c_p = c_v = c $$

Specific Entropy Change of Incompressible Fluids

For an ideal gas with a given, constant specific heat $ c_v $, its change in specific entropy from a state $ 1 $ to a state $ 2 $ is given by the expression

Change in specific entropy

$$ s_2 - s_1 = c_v\ln\frac{T_2}{T_1}+ R \ln\frac{v_2}{v_1} $$

where $ R $ is the gas constant and $ v $ is the specific volume. Assuming this ideal gas is incompressible, $ v_2=v_1 $. Therefore,

$$ s_2 - s_1 = c_v\ln\frac{T_2}{T_1}+ R \ln(1) $$

the ratio of $ \frac{v_2}{v_1}=1 $ and the $ ln(1)=0 $, simplifying the change in specific entropy is

Change in specific entropy for incompressible substances

$$ s_2 - s_1 = c\ln\frac{T_2}{T_1}, $$

as long as $ c $ is constant.