Torsion

Torsion refers to the twisting of a specimen when it is loaded by couples (or moments) that produce rotation about the longitudinal axis. Applications include aircraft engines, car transmissions, and bicycles, etc.

Units

Force X distance [lb-in or N-m]

Notation and Convention

Sign convention

$ \phi > 0 $ : counter clockwise
$ \phi < 0 $ : clockwise

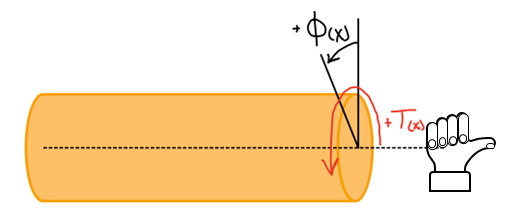
Right hand rule

Torque and angle of twist follow the right hand rule sign convention. When positive, using the right hand, the thumb points outward from the shaft and the fingers will curl in the direction of the positive twist/torque.

Equilibrium

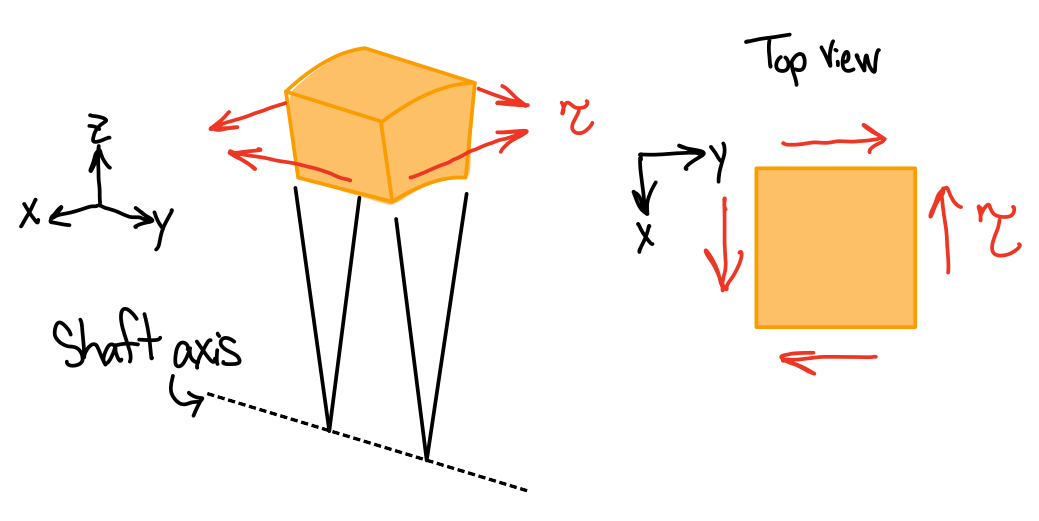
Single element shear stresses

The stress distribution in the shaft is not known.

Statically indeterminate: must consider shaft deformations.
Multi-planar: equilibrium requires the existence of shear stresses on the faces formed by the two planes containing the axis of the shaft

Assumptions

Torsion lines

For circular shafts (hollow and solid): cross-sections remain plane and undistorted due to axisymmetric geometry
For non-circular shafts: cross-sections are distorted when subject to torsion
Linear and elastic deformation

Shear Stress and Strain

Shear Strain: Geometry of Deformation

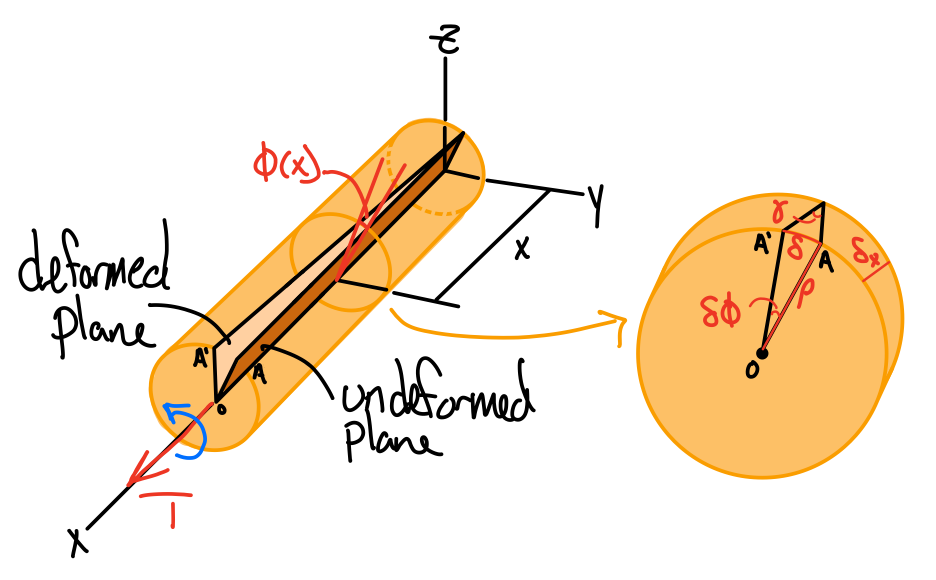
Deformation

The angle of twist increases as x increases.

The twist rate is given by.

$$ \frac{d\phi}{dx} = \frac{\gamma}{\rho} = \frac{\gamma_{max}}{c}\ $$

where $ c $ is the radius and $ \rho $ is a point between 0 and $ c $.

Moving terms.

$$ \gamma = \rho \frac{d\phi}{dx}\ $$

Arc length.

$$ \delta = \rho d\phi\ $$

Hence, the shear strain ($ \gamma $):

is proportional to the angle of twist
varies linearly with the distance from the axis of the shaft
is maximum at the surface

Shear Stress: Torsion Formula

Geometry

$$ \gamma = \rho \frac{d\phi}{dx}\ $$

Hooke's law.

$$ \tau = G\gamma\ $$

From equilibrium.

$$ \frac{d\phi}{dx} = \frac{T}{GJ}\ $$

Elastic torsion formula.

$$ \tau = \frac{T\rho}{J}\ $$

The shear stress in the elastic range varies linearly with the radial position in the section.

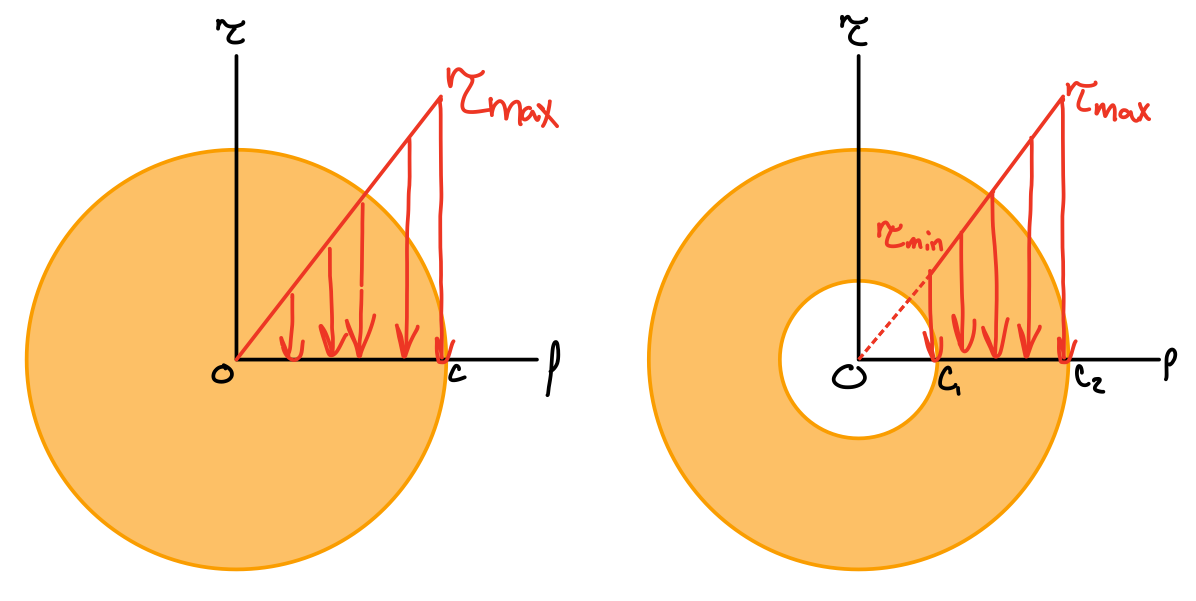
Stress distribution

Note: shaft under torque $ T $ rotating at angular speed $ \omega $ transmits power $ P $.

Power.

$$ P=T\omega\ $$

Shear Stress: Polar Moment of Inertia

Solid shaft (radius and diameter).

$$ J = \int_0^R{\rho^2dA} = \int_0^R{\rho^2(2\pi\rho d\rho)dA} =2\pi \int_0^R{\rho^3d\rho} = \frac{\pi R^4}{2} = \frac{\pi D^4}{32}\ $$

Hollow shaft (inner and outer radius).

$$ J = \frac{\pi}{2}(R_o^4-R_i^4) = \frac{\pi}{32}(D_o^4-D_i^4)\ $$

Heads up!

For a moment of inertia summary, go to the "Moment of Inertia Summary" section of the Bending page.

Shear Stress: Angle of Twist

From observation:

The angle of twist of the shaft is proportional to the applied torque
The angle of twist of the shaft is proportional to the length
The angle of twist of the shaft decreases when the diameter of the shaft increases

Angle of twist.

$$ \phi = \frac{TL}{GJ}\ $$

Torsional stiffness.

$$ k_T = \frac{GJ}{L}\ $$

Torsional flexibility.

$$ f_T = \frac{L}{GJ}\ $$

Miscellaneous

Types of Material Failure

Ductile materials generally fail in shear

Axial – maximum shear stress at $45^o$ angle

Torsion – maximum shear stress at $0^o$ angle

Brittle materials are weaker in tension than shear

Axial – maximum normal stress at $0^o$ angle

Torsion – maximum normal stress at $45^o$ angle

Heads up - Extra!

Torsion of thin-walled hallow shafts builds on this content.

In general, the maximum shear stress is given by

$$ \phi = \frac{TL}{GJ}\ $$

For thin-walled shafts

$$ \tau_{max} = \frac{T}{2tA_m}\ $$

where

$$ \begin{align} A_m &= \pi R_{ave}^2 \\ R_{ave} &= \frac{R_o + R_i}{2} \end{align} $$

Note that is NOT the cross sectional area of the hollow shaft!

Gear Systems

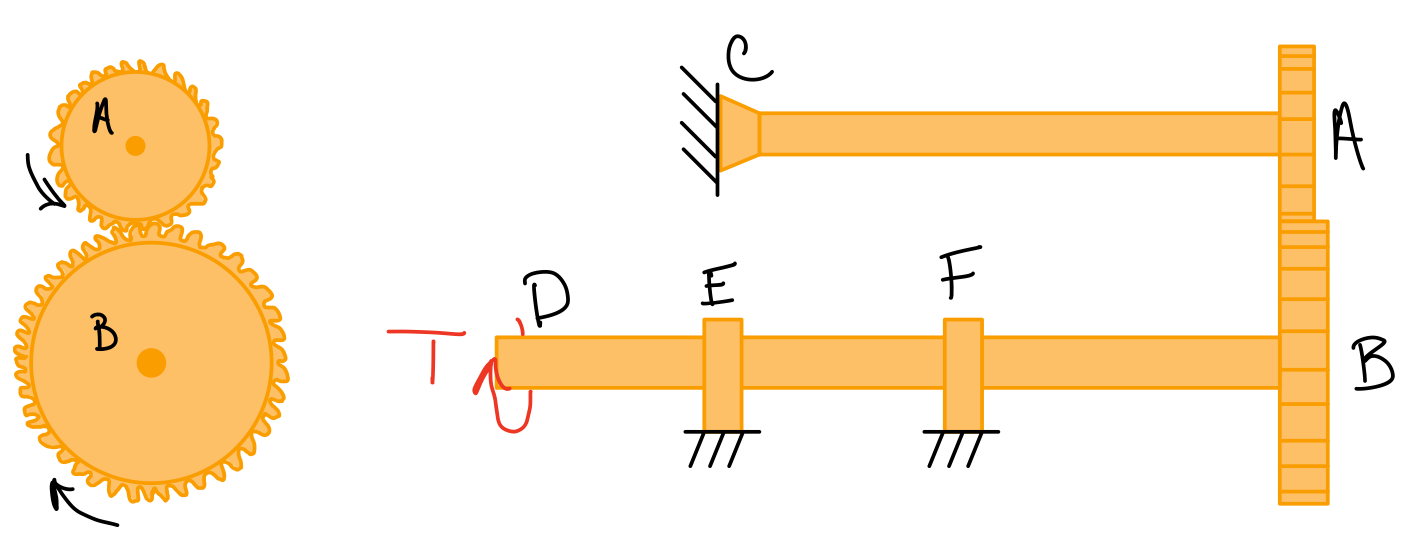
Gear system

Gear system problems can be solved using the torsion equations.

Common assuptions:

Gears are perfectly rigid.
The roation axis is perfectly fixed in space.
Gear teeth are evenly spaced and perfectly shaped so there is no gap to create lost motion.
Gear tooth faces are perfectly smooth so there is no slip.
Mated gears twist through the same arc length.

To solve:

Draw a FBD for each shaft.
Use the torsion equilibrium equations of each shaft to find the recation forces and torques.
Use the shear stress equation to find the stresses in the shaft.

The angle of twist between two mating gears is related through the gear ratio.

Gear ratio.

$$ GR = d_B:d_A\ $$

Angle of twist

$$ \phi_A = GR \text{ } \phi_B\ $$

Note: 1 hp = 550 ft.lb/s

Extra!

Power transmition can be used to find shear stress in gear shafts.

Maximum shear stress:

$$ \tau = \frac{P c}{\omega J}\ $$