Current page:

Force Systems

Equivalent systems

It can be helpful at times to reduce the forces on a body and combine resultant moments and simplify the analysis. Note: These forces and moments will have the same external effect on the body, but the internal forces on the rigid body may be different. For example, the four systems below are statically equivalent, which means that the sum of external forces and sum of extrenal moments are the same for both systems.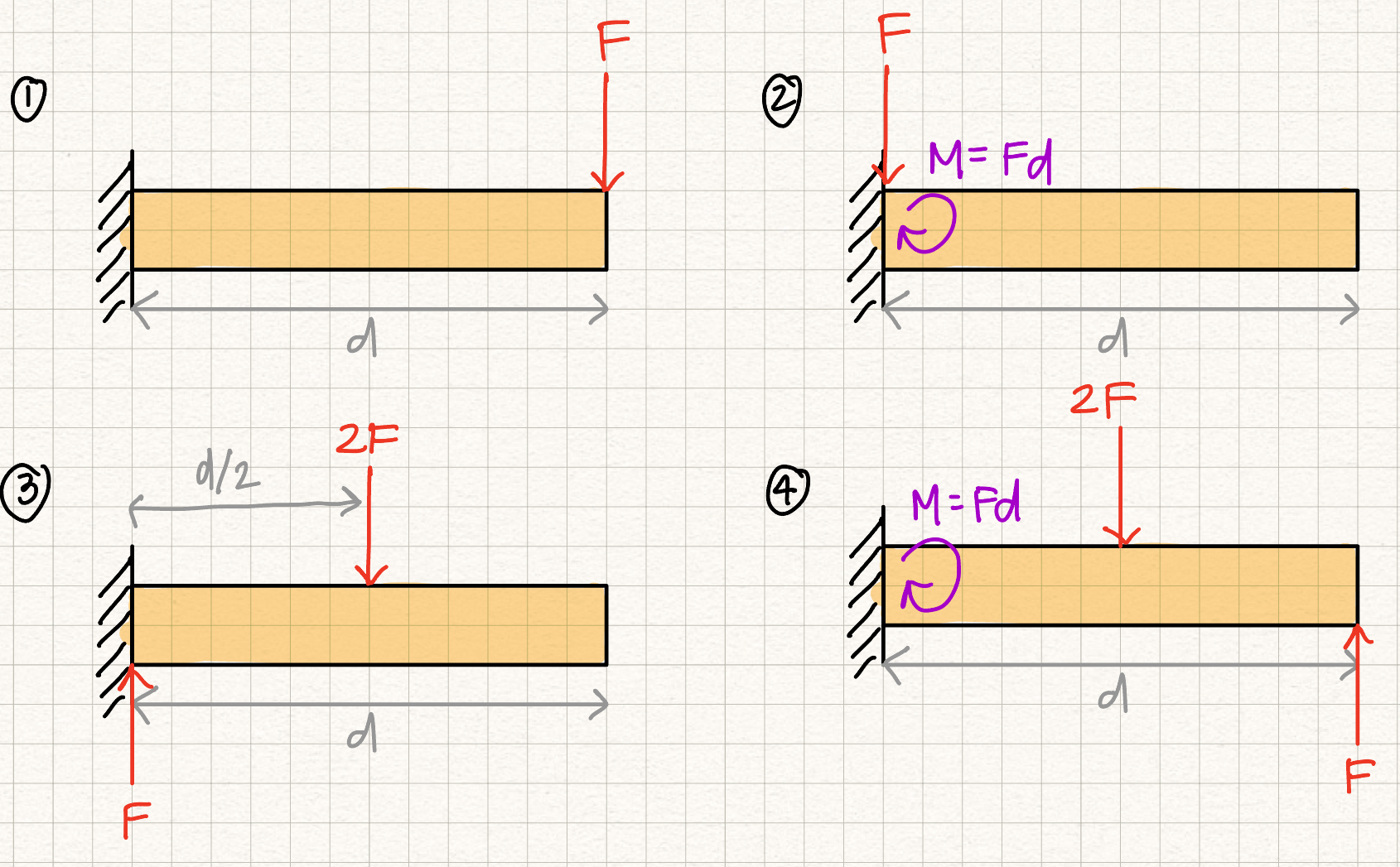

All four of these systems are statically equivalent.

It can be helpful to know what are equivalent transformations for both forces and moments. These are described below:

Allowable Force Transformations

Replacing two forces with their vector sum: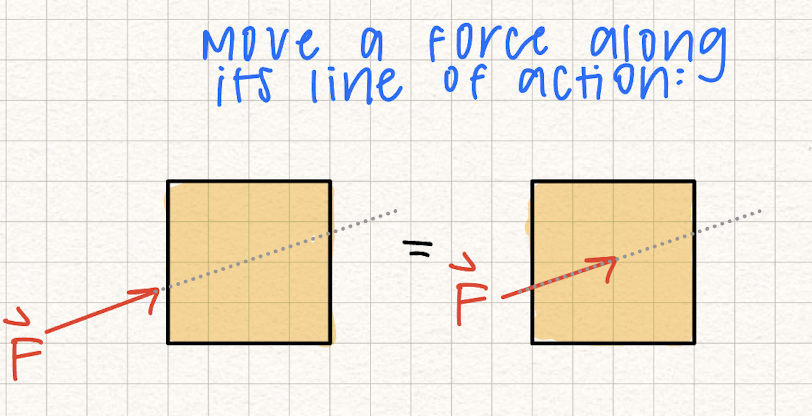

Moving a force ALONG its line of action:

Allowable Moment Transformations

Replacing a force couple with a couple moment: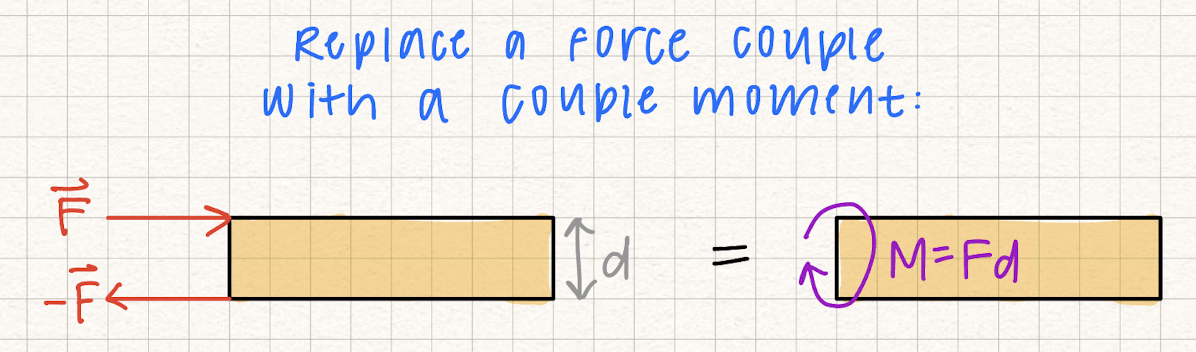

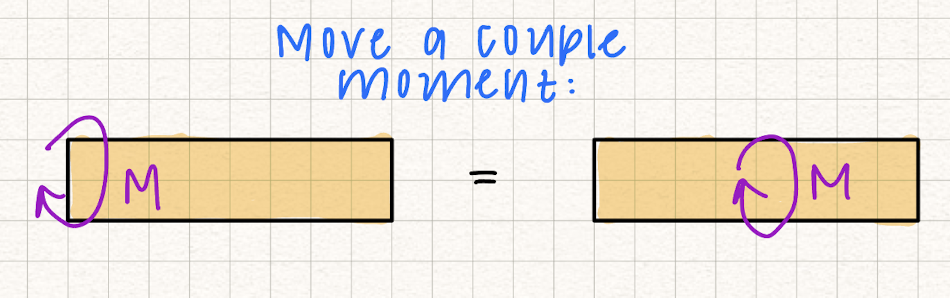
Moving a couple moment to another spot on a rigid body:

Concentrated forces

Concentrated forces are forces acting at a specific point on a body.

A concentrated force applied to a bar at point A.

Distributed loads

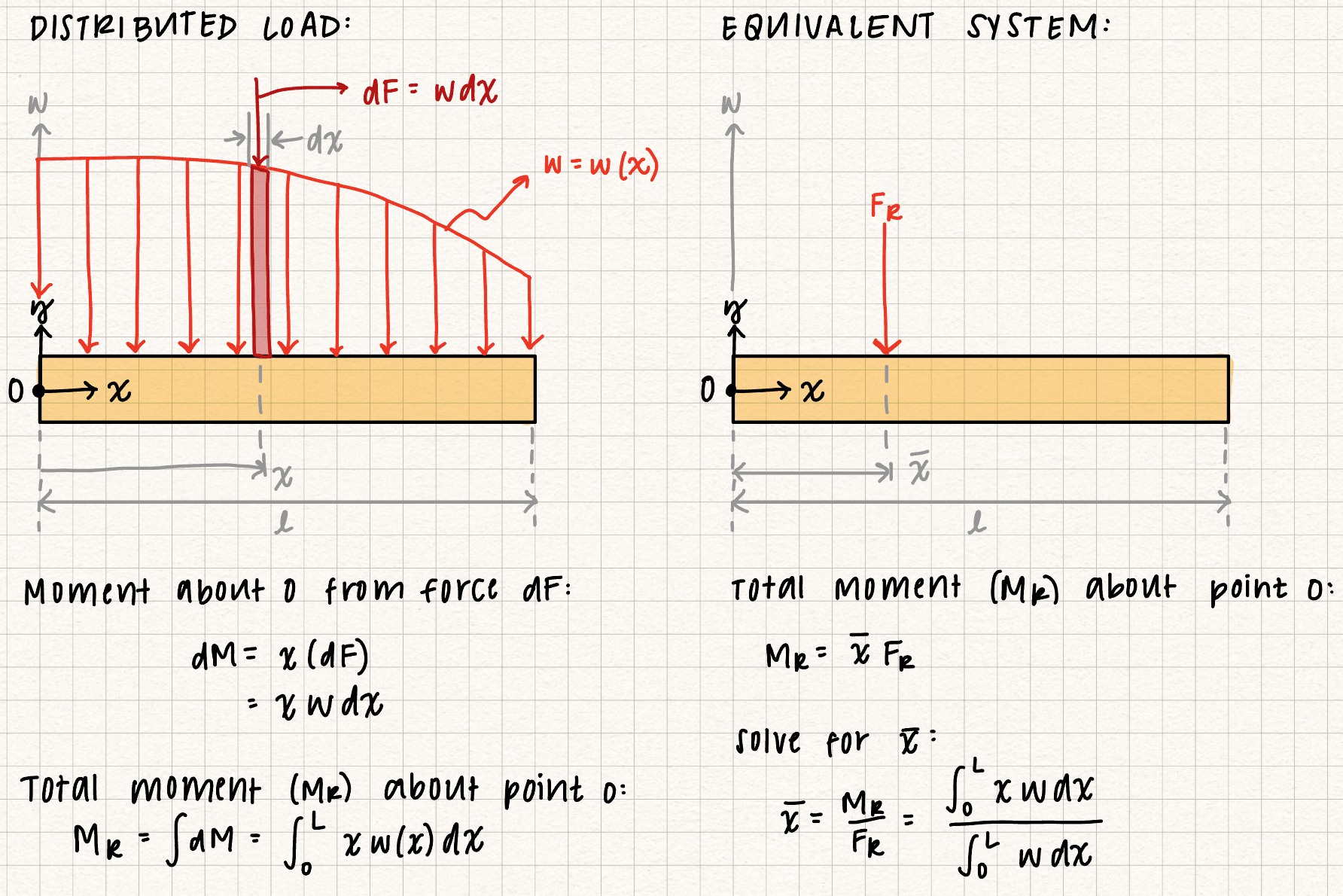
Distributed loads (usually written as $ w(x) $) are forces applied over a length, volume, or area. The SI units for distributed loads are N/m. These loads, written as a function of length $ x $ can be simplified into an equivalent force, $ F_R $, which results in the same external loading on the rigid body. The magnitude of the equivalent force $ F_R $ is the area under the $ w(x) $ curve. The location of the resultant force $ F_R $ is the location of the centroid of the shape of the force curve.

Rectangular loading

For a constant distributed load of magnitude c applied to a bar over a length l, the resultant force magnitude is

$$ F_R = c*l\ $$

the resultant force location is at $ l/2 $.

Example distributed load (top) and its equivalent force system (bottom).

Triangular loading

For a triangular distributed load (a uniformly varying load), the magnitude of the load is equivalent to the area of the triangle.

$$ F_R = 0.5*c*l\ $$

The location of $ F_R $ is 1/3 from the base of the triangle.

Example triangular distributed load (top) and its equivalent force system (bottom).

Nonuniform distributed loads

More complex distributed loads can be reduced to two distributed loads of uniform shape, or the integral of the distributed load function can be taken to obtain the area under $ w(x) $, which is $ F_R $.

$$ F_R = \int_{0}^{L} w(x) \,dx \ $$

The location of $ F_R $ on the beam can be found by solving for the moment $ M_R $ about a point. In this case we will take the moment about the point $ x $=0 and setting it equivalent to the moment produced by the resultant force $ F_R $ at $ x $=0.

$$ M_R = \int_{0}^{L} x*w(x) \,dx = \bar{x}*F_R\ $$

Now we can solve for the center of mass of the distributed load, $ \bar{x} $, using

$$ \bar{x} = \dfrac{M_R}{F_R}\ $$

Nonuniform load.