Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Current page:

    Thermodynamic Terminology and Definitions

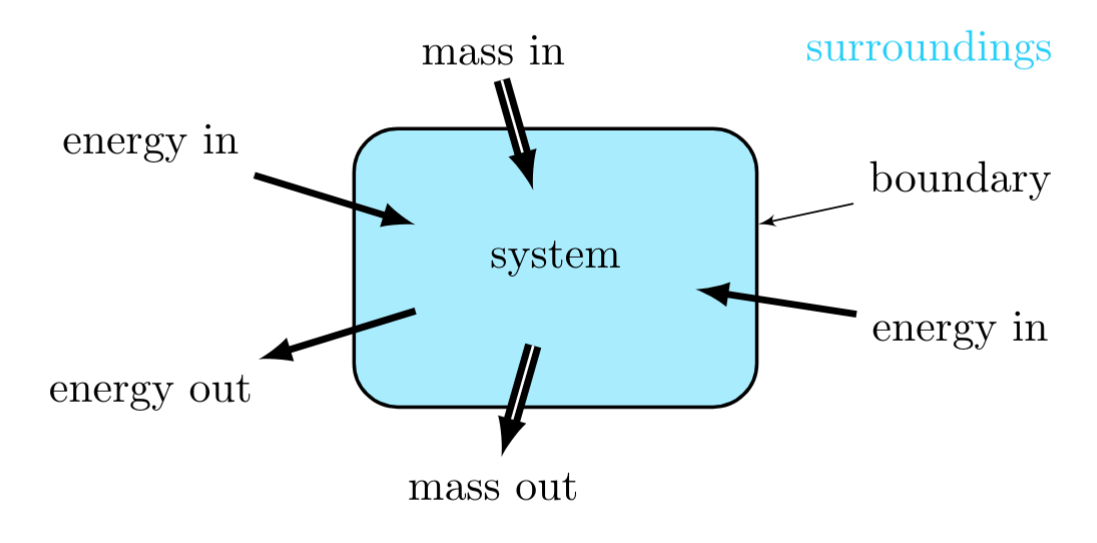
    System, boundaries and surroundings

    Energy and matter flow between a thermodynamic system and its surroundings that are separated by a boundary, lead to changes its internal state. An increase in its mass results when the matter flowing into the system is greater than that flowing out of the system. An increase in its internal energy results when the energy flowing into the system is greater than that flowing out of the system. When the flow rates into and out of the system are equal, the system is in a steady state.

    Figure1: A schematic representation of a thermodynamic system illustrating its key features including depictions of energy and mass flows.

    Steady-state:

    When the flow rates into and out of the system are equal, the system is in a steady state

    Transient:

    The state of a thermodynamic system is transient if it is not in steady state.

    Types of Systems: Closed, Open, and Isolated Systems

    Closed System:

    Mass cannot flow in or out of the system, therefore energy is transferred via only heat or work.

    Open System:

    An open system can exchange both energy and matter with its surroundings.

    Isolated System:

    A system is isolated from its environment, meaning neither matter nor energy may flow in or out of the system.

    Units of Interest

    Typical Units in SI and English Systems

    Typical Units in SI and English Systems: Dimensions

    DimensionSIUS
    Lengthmeter (m)foot (ft)
    Masskilogram (kg)pound mass (lb)
    Timesecond (s)second (s)

    Typical Units in SI and English Systems: State properties

    State propertySIUS
    Pressure1 Pa = N/m\( ^2 \) = J/m\( ^3 \)
    Volumem\( ^3 \)ft\( ^3 \)
    Temperaturedegrees Celcius (\( ^{\circ} \)C)degrees Fahrenheit (\( ^{\circ} \)F)
    Absolute TemperatureKelvin (K)degree Rankine (\( ^{\circ} \)R)
    Internal Energy, EnthalpyJoules (J)British thermal Unit (Btu)
    Newton-meter (N\( \cdot \)m)Foot-pound force (ft\( \cdot \)lbf)
    Entropy(J/K)Btu/\( ^{\circ} \)R

    Useful Conversions

    Pressure

    Pressure unit conversions
    $$ \begin{aligned} 1~\textrm{standard atm} &= 1.01325 ~\textrm{bar} = 1.01325 \times 10^{5} ~\textrm{Pa} = 14.696~\textrm{psi} \\ &= 760~\textrm{mmHg} = 29.92~\textrm{inHg}\end{aligned} $$

    Temperature

    Temperature unit conversions
    $$ \begin{aligned}\textrm{Fahrenheit to Rankine:}&~ ^{\circ}\textrm{R} = ^{\circ}\textrm{F} + 459.67 \\ \textrm{Celsius to Kelvin:}&~ ^{\circ}\textrm{K} = ^{\circ}\textrm{C} + 273.15\end{aligned} $$

    Energy

    Energy unit conversions
    $$ \textrm{Btu to ft\(\cdot\)lbf:}~ 1~\textrm{Btu} = 778.18~ \textrm{ft}\cdot\textrm{lbf} $$

    Useful Constants

    Gravity

    Mass to force conversions (Earth specific)
    $$ \begin{aligned} 9.8~\textrm{N} = 1~\textrm{kg}\times 9.8~ \textrm{m}/\textrm{s}^2 \\ 1~\textrm{lbf} = 1~\textrm{lb}\times 32~ \textrm{ft}/\textrm{s}^2 \end{aligned} $$

    Universal Gas Constant, \( \overline{R} \)

    Universal Gas Constant in different units
    $$ \begin{aligned} \overline {R} = 8.314~\textrm{kJ/kmol}\cdot \textrm{K} \\ \overline {R} = 1545~\textrm{ft}\cdot \textrm{lbf}/\textrm{lbmol}\cdot ^{\circ}\textrm{R} \\ \overline {R} = 1.986~\textrm{Btu}/\textrm{lbmol}\cdot ^{\circ}\textrm{R} \end{aligned} $$

    Molecular weights \( M \) of common substances:

    Note: (1 g/mol = 1 kg/kmol = 1 lb/lbmol): \( R= \frac{\overline{R}}{M} \)

    Convert this to a table??
    • Air- 28.97 g/mol
    • Carbon dioxide CO\( _2 \)- 44.01 g/mol
    • Ethane C\( _2 \)H\( _6 \)- 30.07 g/mol
    • Hydrogen H\( _2 \)- 2.01 g/mol
    • Methane CH\( _4 \)- 16.04 g/mol
    • Nitrogen N\( _2 \)- 28.01 g/mol
    • Oxygen O\( _2 \)- 32.00 g/mol
    • Refrigerant 22- 86.48 g/mol
    • Refrigerant 134a- 102.3 g/mol
    • Water H\( _2 \)O- 18.015 g/mol

    Helpful Math Expressions

    Integrals:

    Integral of the inverse function
    $$ \int_{y_a}^{y_b} \frac{1}{y}dy = ln(y)|_{y_a}^{y_b} $$
    Power rule with negative exponents \(\neq\) -1
    $$ \int_{y_a}^{y_b} \frac{1}{y^{\gamma}}dy = - \left. \frac{1}{\gamma -1}\frac{1}{y^{\gamma -1}} \right|_{y_a}^{y_b} ,~\textrm{for}~\gamma \neq 1 $$

    Natural Logs:

    Additive property of logarithms
    $$ ln(ab)= ln(a)+ln(b) $$
    Change of base of exponentials
    $$ e^{aln(b)} = b^a $$

    Mass and Mass Flow

    As matter flows in and out of a thermodynamic system, the amount of mass in the system at time \( t \) by is defined by \( m(t) \), then

    Mass-balance differential equation
    $$ \frac{dm}{dt}(t) = \sum_{in}\dot{m}_{in}(t) - \sum_{out}\dot{m}_{out}(t), $$

    refers to 'the rate of change of the mass of the system.' The sums on the right add up all mass flows into and out of the system, respectively. If this quantity is positive, then the mass of the system is increasing. If it is negative, the mass of the system must be decreasing, as long as there is still mass left inside the system.

    If these flow rates are known functions of time, then this equation implies that

    Mass-balance equation #MassBalanceInt
    $$ m(t) = m(0) + \int_0^t \left( \sum_{in}\dot{m}_{in}(\tau) - \sum_{out}\dot{m}_{out}(\tau)\right) d\tau, $$

    where \( m(0) \) is the initial value of the mass in the system at time \( t=0 \). Integrating Eqn. MassBalanceInt with respect to time yields.

    Result of mass-balance equation #MassBalanceInt2
    $$ m(t) - m(0) = \Delta m = \sum_{in}m_{in}- \sum_{out}m_{out} $$
    where \( m_{in} \) and \( m_{out} \) are the total quantities of mass transferred in or out of the system for a given set of processes.
    Figure2: A system whose state is changing due to mass flow.

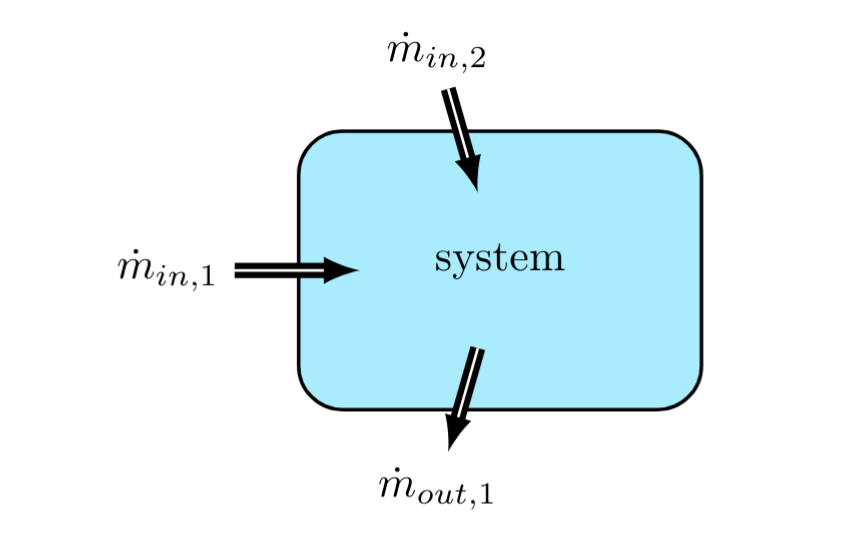
    Given the thermodynamic system shown in Figure 2, one can write the rate of change of mass of the system equals the following quantity,

    $$ \dot{m}_{in,1} +\dot{m}_{in,2} - \dot{m}_{out,1} $$

    Volume and Volume Flow

    The volume \( V \) of a system is an extensive parameter for describing its thermodynamic state. The specific volume \( v \), an intensive property, is the system's volume per unit mass. Volume is a function of state and is interdependent with other thermodynamic properties such as pressure and temperature.

    Specific Volume

    Specific volume is the volume per unit mass

    Specific volume equation and units
    $$ v=\frac{V}{m}={\frac{\textrm{m}^3}{\textrm{kg}}} $$

    Volume Flow

    As mass flows into a system, energy increases by the addition of both the internal energy of the additional mass and the \( pV \) work done by the volume occupied by the mass on the system as it enters, and vice versa.

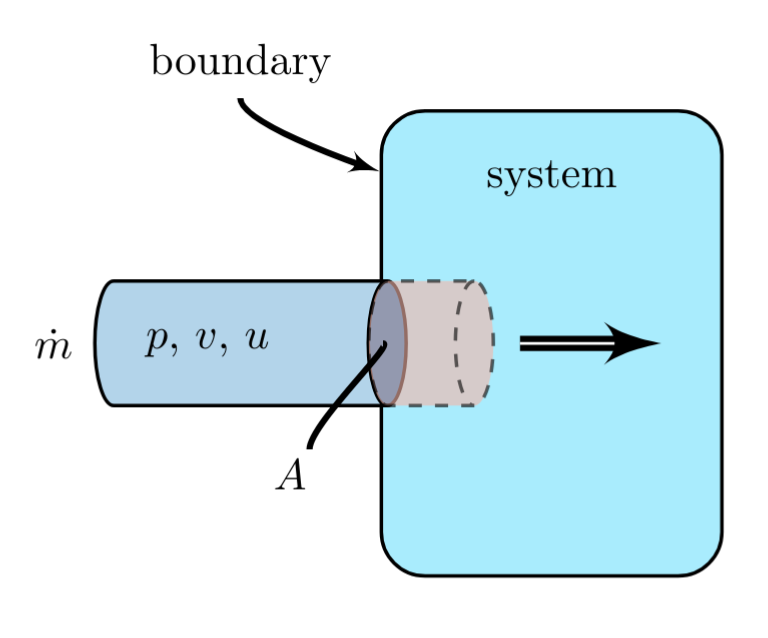
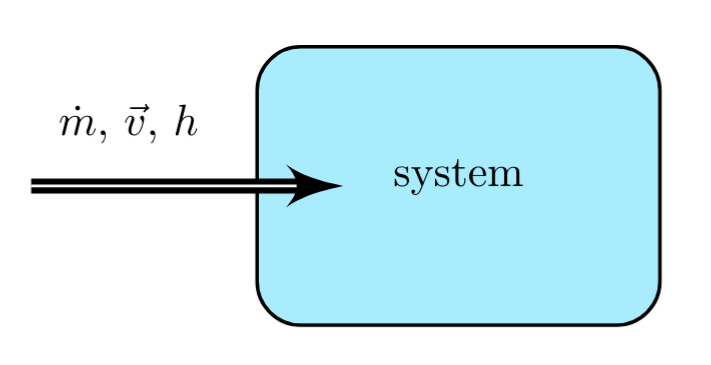
    A mass flow having rate \( \dot{m} \) with cross-sectional area, \( A \), slowly enters a system. The mass is at a pressure \( p \), has a specific volume \( v \), and has a specific internal energy, \( u \), relative to some reference state.

    The mass flows into the system, over a given time interval \( \Delta t \), increasing the internal energy of the system as it enters, by:

    Mass-flow & internal energy relationship #Deltau_dotm
    $$ \dot{m}\Delta t u=mu. $$

    The volume occupied by the portion of the stream entering a system is defined by,

    Volume in-flow
    $$ V_{\text{in-flow}}=\dot{m}\Delta t v=mv $$

    This volume is pushed at constant pressure, \( p \), into the system, is doing \( pV \) work on the system, which will be described further in section \(pV\) work.

    Energy and Energy Flow

    Internal Energy

    The internal energy, \( U \), of a thermodynamic system relative to some reference state \( U_0 \) is the energy required to set up the positions and motions of the atoms and molecules within the system from their positions and motions in the reference state. When the system is in its reference state, its relative internal energy equals \( 0 \).

    External energy balance
    $$ \Delta U = U - U_0 = \textrm{energy}_{in} - \textrm{energy}_{out} $$

    The addition of energy to a system in its reference state will result in the system having a positive relative internal energy. The removal of energy from a system in its reference state will result in the system having a negative relative internal energy. Eqn.MassBalanceInt2.

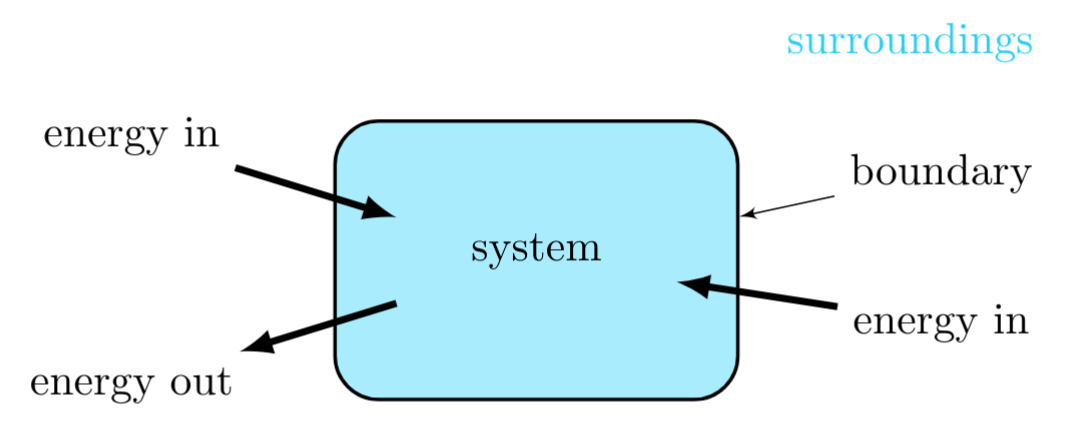
    Figure 3: A schematic representation of a thermodynamic system illustrating energy flows.

    Internal Energy Contributions

    The internal energy (\( U \)) of a system is affected by the energetic contributions from heat flow (\( Q \)) in and out of a system and work (\( W \)) done by or on a system.

    Internal energy balance
    $$ \Delta U = Q - W. $$

    Sign Convention:

    These energetic changes affect thermodynamic systems as follows:

    1. When heat is transferred to the system, the system energy increases (positive heat transfer).
    2. When the system does work on its surroundings, the system energy decreases (negative sign in front of work done by system).
    3. When the system transfers heat to the surroundings, the system energy decreases (negative heat transfer).
    4. When work is done on to the system, the system energy increases (positive sign in front of work done on system).
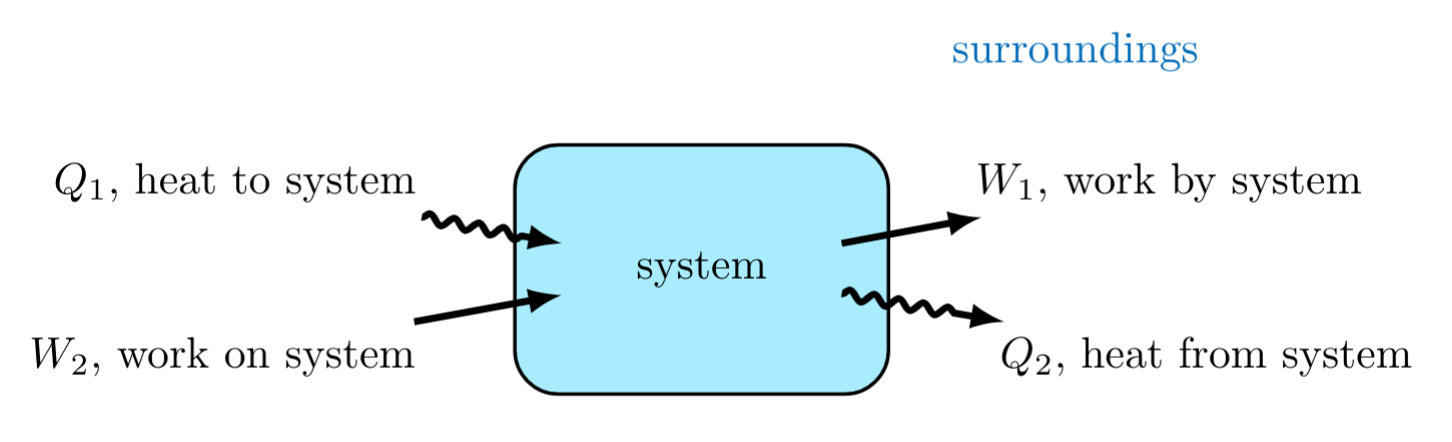
    Figure 4: A schematic illustrating the direction of energy flow when heat is transferred to/from the system and work is performed on or by the system.

    Given the system shown in Figure 4, the net work done by the system is \( W_1-W_2 \). The net heat transferred to the system is \( Q_1-Q_2 \). The change in system energy is

    Change in total system energy
    $$ \Delta U = Q_1-Q_2-(W_1-W_2). $$

    Potential Energy

    A system may find itself subject to a conservative force in a position that differs from a reference position. In this scenario, work has been done against a conservative force, such as changing the height, \( h \), to change the potential energy.

    Typical conservative forces include elastic potential energy, e.g., a spring, and electric potential energy. For the particular case of gravity,
    Potential energy
    $$ \begin{split}W_{\text{PE}_g}&=\int_{z_1}^{z_2}mg\,dz\\&=mg(z_2-z_1)\end{split} $$

    Thus the change in the gravitational potential energy of the system.

    Work done by potential energy
    $$ W_{\text{PE}_g}=\Delta \text{PE}_g $$

    Kinetic Energy

    A system may find itself in motion with respect to a reference frame. In this first case, work has been done to

    accelerate the system to its velocity. Work done is defined by forces acting over a distance, and work \( W_{\text{KE}} \) can be done to accelerate the system to its velocity,

    Work-force relationship
    $$ W_{\text{KE}}=\int_{\vec{x_1}}^{\vec{x_2}}\vec{f}\,d\vec{x}. $$

    Force is determined from Newton's 2nd law:

    Newton's second law
    $$ \vec{f}=m\frac{d\vec{v}}{dt}=m\frac{d\vec{v}}{d\vec{x}}\underbrace{\frac{d\vec{x}}{dt}}_{\vec{v}}=m\vec{v}\frac{d\vec{v}}{d\vec{x}} $$

    This results in the following relationship for work done via kinetic energy change (\( W_{\text{KE}} \))

    Work-momentum relationship
    $$ \begin{split}W_{\text{KE}}&=\int_{\vec{v_1}}^{\vec{v_2}}m\vec{v}\,d\vec{v}\\&=\frac{1}{2}m(\vec{v}_2^2-\vec{v}_1^1).\end{split} $$

    Thus the change in kinetic energy of the system.

    Work done by kinetic energy
    $$ W_{\text{KE}}=\Delta \text{KE} $$

    Enthalpy

    Enthalpy is a state function that is the sum of a system's internal energy \( \mu \) and the product of its pressure and volume \( pv \).

    Relative Specific Enthalpy

    The sum \( u+pv \) appears frequently in thermodynamic discussion so it is conveniently defined as relative specific enthalpy \( h \), consisting of the same atomic and molecular kinetic and potential energies as specific internal energy \( u \), but with the addition of flow work, \( pv \)

    Relative enthalpy #RelativeEnthalpy
    $$ h=u+pv. $$

    Entropy

    The topic of entropy is discussed on this page.