Contact and rolling
Rolling motion
A special case of rigid body motion is rolling without slipping on a stationary ground surface. This is defined by motion where the point of contact with the ground has zero velocity, so it matches the ground velocity and is not slipping.
It is helpful to think about the motion of the body in two ways:
- The body rotates about the moving center \( C \).
- The body rotates about the instantaneous center at the contact point \( P \).
These two ways of visualizing the motion can be seen on the figure below.
Movement:
flat
big flat
rock
inside 2-circle
inside 3-circle
inside rock
outside 1-circle
outside 2-circle
outside rock
Center \(C\)
Body
\(P\) velocity
none
\( \vec{v}_C \) (trans.)
\( \vec{\omega} \times \vec{r}_{CP} \) (rot.)
\( \vec{v}_P \) (total)
\(P\) acceleration
none
\( \vec{a}_C \) (trans.)
\( \vec{\alpha} \times \vec{r}_{CP} \) (ang.)
\( \vec{\omega} \times (\vec{\omega} \times \vec{r}_{CP}) \) (cent.)
\( \vec{a}_P \) (total)
Velocity and acceleration of points on a rigid body undergoing different rolling motions.
Heads up!
Instant centers builds on this content in mechanism design.
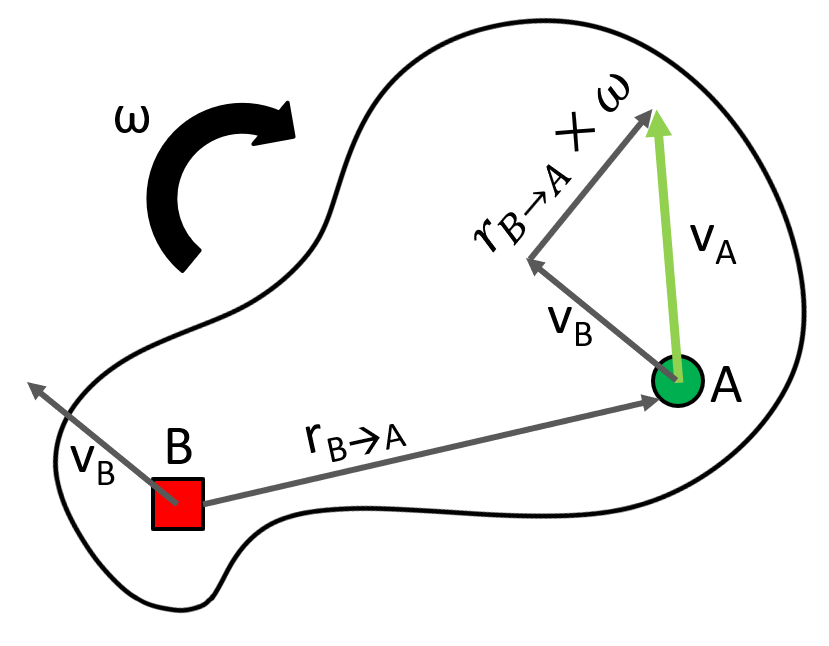
Any rigid body has an angular velocity, which can create a linear velocity.
Rolling on a flat surface
The most common and also the simplest form of rolling occurs on a flat surface.
Geometry and variables for rolling without slipping on a flat surface.
While rolling, the velocity and acceleration are directly connected to the angular velocity and angular acceleration, as shown by the next equations.
Another way to express the connection between angular and linear velocity and acceleration is via the distance \(s\) traveled by the rolling body:
While rolling, the contact point will have zero velocity but will have a centripetal acceleration towards the rolling center:
Rolling on curved surfaces
When a circular rigid body rolls without slipping on a surface which is itself curved, the radius of curvature of the surface affects the acceleration (but not velocity) of points on the rolling body.
The center velocity for rolling on a curved surface is the same as for a flat surface, while the acceleration also depends on the radius of curvature of the surface:
Just as with rolling on a flat surface, when a rigid body rolls on a curved surface the contact point has zero velocity but nonzero acceleration, as shown below.