Rigid Body Kinetics

Center of mass (COM)

The total mass of a rigid body is as follows:

Total mass of a rigid body. #rcm-tm

$$ m = \iiint_{\mathcal{B}} \rho \, dV $$

The mass of an infinitesimally small element of the rigid body $dm$ assuming constant density is: \[ dm = \rho \, dV \] Therefore, integrating over the entire volume of the body gives us the expression above.

The center of mass of a rigid body can be calculated as follows:

Center of mass $C$ of a rigid body. #rcm-cm

$$ \begin{gathered} \vec{r}_C = \frac{1}{m}\iiint_{\mathcal{B}} \rho \vec{r} \, dV \\ \end{gathered} $$

$ \vec{r} $ is the vector from a reference origin $ O $ to $ dV $.

The integral term $ \iiint_{\mathcal{B}} \rho \vec{r} \, dV $ is known as the "first moment of mass".

The center of mass of a collection of particles is given by the finite sum:

$$ \vec{r}_C = \frac{1}{m} \sum_{i=1}^{N} m_i \, \vec{r}_i $$

Therefore, for a continuous mass distribution and infinite number of particles, the sum becomes an integral and the masses become the mass of an infinitesimally small element on the rigid body:

$$ \vec{r}_C = \frac{1}{m}\iiint_{\mathcal{B}} \vec{r} dm $$

Where $ dm = \rho \, dV $ from the differential of #rcm-tm. Substituting in:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iiint_{\mathcal{B}} \vec{r} dm \\ &= \frac{1}{m}\iiint_{\mathcal{B}} \vec{r} \rho \, dV \\ &= \frac{1}{m}\iiint_{\mathcal{B}} \rho \vec{r} \, dV \\ \end{aligned} $$

Example Problem: Center of mass of a right-triangular plate. #rcm-xc

A solid uniform right-triangular plate with mass $ m $ has width $ w $, height $ h $. Where is the center of mass $ \vec{r}_C $located?

In order to figure out where the center of mass is located, we will need to choose an origin. The origin chosen in this instant is where the base and height begin, as shown. Using the center of mass formula will allow us to calculate the vector shown below (i.e we are calculating $ \vec{r}_{OC} $).

Using the formula #rcm-cm:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m} \iiint_{\mathcal{B}} \rho \vec{r} \, dV \\ &= \frac{1}{m} \iint_{A} \rho \vec{r} \, tdA \\ \end{aligned} $$

Where $ A $ represents the surface area of the plate, and $ t $ is the thickness. We will assume the thickness is 1, as we are only interested in the center of mass in the $ x $-$ y $ plane. Our triple integral with $ dV $instead becomes a double integral with $ dV = t dA $. We therefore have:

$$ \vec{r}_C = \frac{1}{m} \int_{x_1}^{x_2} \int_{y_1}^{y_2} \rho \vec{r} \, dA $$

We will redraw the figure and show the $dA$ element. We will also find the $x$-coordinate and $y$-coordinate ranges for the body.

Examining the figure above, we can see that the $ x $-coordinate range is $ 0 $ to $ w $. Our $ y $-coordinate range has a dependence on the $ x $-value, and the equation of the hypotenuse is $ y = h - \frac{h}{w}x $, using the point-slope formula. Therefore, the $ y $-coordinate range is $ 0 $ to $ h - \frac{h}{w}x $. As a result of this, we will have to integrate with respect to $ y $ first. All in all, our center of mass equation becomes:

$$ \vec{r}_C = \frac{1}{m} \int_{0}^{w} \int_{0}^{h - \frac{h}{w}x} \rho \vec{r} \, dydx $$

where $ vec{r} $ is the distance to the $ dA $ element. We can see the coordinates of $ dA $ are $[x,y]$. Thus, $ \vec{r} = x\hat{\imath} + y\hat{\jmath} $. Therefore:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m} \int_{0}^{w} \int_{0}^{h - \frac{h}{w}x} \rho \left(x\hat{\imath} + y\hat{\jmath}\right) \, dydx \\ &= \frac{\rho}{m} \int_{0}^{w} \int_{0}^{h - \frac{h}{w}x} \left(x\hat{\imath} + y\hat{\jmath}\right) \, dydx \\ &= \frac{\rho}{m} \left[\int_{0}^{w} \int_{0}^{h - \frac{h}{w}x} \left(x\hat{\imath} \, dy\right)dx + \int_{0}^{w} \int_{0}^{h - \frac{h}{w}x} \left(y\hat{\jmath} \, dy\right)dx\right] \\ &= \frac{\rho}{m} \left[\int_{0}^{w} x\left(h - \frac{h}{w}x\right)\hat{\imath}dx + \int_{0}^{w} \frac{1}{2}\left(h - \frac{h}{w}x\right)^2\hat{\jmath}dx\right] \\ &= \frac{\rho}{m} \left[\frac{w^2 h}{6}\hat{\imath} + \frac{wh^2}{6}\hat{\jmath}\right] \end{aligned} $$

where $ \frac{\rho}{m} = \frac{1}{A} = \frac{1}{\frac{1}{2}wh} = \frac{2}{wh} $. Substituting that in yields:

$$ \vec{r}_C = \frac{1}{3}w \hat{\imath} + \frac{1}{3}h \hat{\jmath} $$

Meaning the center of mass for a right-triangular plate is located at 1/3rd of the width, and 1/3rd of the height. This formula has been used to calculate the center of mass of different common shapes.

Finding the center of mass allows us to treat complex shapes as point-masses with all their mass at the center of mass.

To find the center of mass of a body made up of composite shapes, we simply do the weighted average of each body by using the fact above.

Center of mass (C) of composite bodies. #rcm-cb

$$ \vec{r}_C = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1 + m_2} $$

$ \vec{r}_i $ is the center of mass of the $i$th body. The whole body $ \mathcal{B} $ is composed of sub-bodies $ \mathcal{B}_1 $ and $ \mathcal{B}_2 $

Finding the center of mass of the whole body follows directly from the fact that the integral over the whole body is the sum of the integrals over the sub-bodies. That is, for $ \mathcal{B} = \mathcal{B}_1 \cup \mathcal{B}_2 $ (and $ \mathcal{B}_1 $not overlapping with $ \mathcal{B}_2$ $, we have:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{M}\iiint_\mathcal{B} \rho \vec{r} \, dV \\ &= \frac{1}{M}\iiint_{\mathcal{B}_1 \cup \mathcal{B}_2} \rho \vec{r} \, dV \\ &= \frac{1}{M}\left[\iiint_{\mathcal{B}_1} \rho_1 \vec{r}_1 \, dV + \iiint_{\mathcal{B}_2} \rho_2 \vec{r}_2 \, dV \right] \\ &= \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{M} \\ &= \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1 + m_2} \end{aligned} $$

Example Problem: Center of mass of an L-shaped plate. #rcm-xl

A solid uniform L-shaped plate has mass $m$ and dimensions as shown. What is the location of the center of mass?

In order to figure out where the center of mass is located, we will need to choose an origin. The origin chosen here is the corner shown.

Then we must realize that the L-shape can be decomposed into four square plates, as shown. Each square plate has the same mass, so:

$$ m_i = \frac{1}{4}m $$

Using the addition formula #rcm-cb:

$$ \vec{r}_C = \frac{1}{m} \sum_{i=1}^{4} m_i \vec{r}_i $$

where:

$$ \begin{aligned} \vec{r}_1 &= d\hat{\imath} + 3d\hat{\jmath} \\ \vec{r}_2 &= d\hat{\imath} + d\hat{\jmath} \\ \vec{r}_3 &= 3d\hat{\imath} + d\hat{\jmath} \\ \vec{r}_4 &= 5d\hat{\imath} + d\hat{\jmath} \end{aligned} $$

Substituting in:

$$ \begin{aligned} x_C = \frac{\frac{1}{4}md + \frac{1}{4}md + \frac{3}{4}md + \frac{5}{4}md}{m} = \frac{5}{2}d \\ y_C = \frac{\frac{3}{4}md + \frac{1}{4}md + \frac{1}{4}md + \frac{1}{4}md}{m} = \frac{3}{2}d \end{aligned} $$

Thus, the center of mass of the L-shape plate:

$$ \vec{r}_C = \frac{5}{2}d \hat{\imath} + \frac{3}{2}d \hat{\jmath} $$

And its location on the plate is shown below.

Recap

Type of shape	Operation
Simple shapes	Symmetry tables
Combination of simple shapes	Find each c.o.m and then combine
Complex shapes	Integrate

Basic Shapes

The centers of mass listed below are all computed directly from the integral #rcm-cm. Note the center of mass provided is the vector from point $O$ (the reference origin).

Rectangular plate: center of mass #rcm-er

$$ \vec{r}_C = \frac{\ell_x}{2}\hat{\imath} + \frac{\ell_y}{2}\hat{\jmath} $$

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iiint_\mathcal{B} \rho \vec{r} \, dV \\ &= \frac{1}{m}\iint_{A} \rho \vec{r} \, dA \\ &= \frac{\rho}{m}\int_{0}^{\ell_x}\int_{0}^{\ell_y} \left[x\hat{\imath} + y\hat{\jmath}\right] \, dydx \\ &= \frac{\rho}{m}\int_{0}^{\ell_x} \left[xy\hat{\imath} + \frac{y^2}{2}\hat{\jmath}\right]_{y = 0}^{y = \ell_y} dx \\ & = \frac{\rho}{m}\int_{0}^{\ell_x} \left[x\ell_y \hat{\imath} + \frac{\ell^2_y}{2}\hat{\jmath}\right]dx \\ & = \frac{\rho}{m} \left[\frac{x^2}{2}\ell_y \hat{\imath} + \frac{\ell^2_y}{2}x\right]_{x = 0}^{x = \ell_x} \\ & = \frac{\rho}{m} \left[\frac{\ell_y \, \ell^2_x}{2} \hat{\imath} + \frac{\ell^2_y \, \ell_x}{2} \hat{\jmath}\right] \\ \end{aligned} $$

The total mass of the plate is $ m = \rho A = \rho \ell_x \ell_y $. Thus we have:

$$ \vec{r}_C = \frac{\ell_x}{2}\hat{\imath} + \frac{\ell_y}{2}\hat{\jmath} $$

Triangular plate: center of mass #rcm-et

$$ \vec{r}_C = \frac{x_P + x_Q}{3}\hat{\imath} + \frac{y_Q}{3}\hat{\jmath} $$

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iiint_\mathcal{B} \rho \vec{r} \, dV \\ &= \frac{1}{m}\iint_{A} \rho \vec{r} \, dA \\ \end{aligned} $$

It is convenient to do a linear transformation from $x$-$y$ plane to the $u$-$v$ plane, to transform the triangle into a right-triangle with $b = 1$, $h = 1$:

$$ \begin{aligned} x &= au + bv \\ y &= cu + dv \\ \end{aligned} $$

Or solve the following system of equations:

$$ \begin{aligned} x_P &= a(1) + b(0) \\ x_Q &= a(0) + b(1) \ y_P &= c(1) + d(0) \\ y_Q &= c(0) + d(1) \\ \end{aligned} $$

We find that the linear transformation is:

$$ \begin{aligned} x &= x_P u + x_Q v \\ y &= y_P u + y_Q v \\ \end{aligned} $$

The Jacobian of this coordinate transformation is:

$$ \begin{aligned} J &= \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} x_P & x_Q \\ y_P & y_Q \end{vmatrix} = x_P y_Q - x_Q y_P \end{aligned} $$

Starting with the $x$-coordinate:

$$ \begin{aligned} x_C &= \frac{\rho}{m}\int_{0}^{1}\int_{0}^{1 - u} (x_P u + x_Q v) \, J \, dvdu \\ &= \frac{\rho}{m}\int_{0}^{1}\int_{0}^{1 - u} (x_P u + x_Q v) \, (x_P y_Q - x_Q y_P) \, dvdu \\ &= \frac{\rho}{m}(x_P y_Q - x_Q y_P)\int_{0}^{1}\int_{0}^{1 - u} (x_P u + x_Q v) \, dvdu \\ &= \frac{\rho}{m}(x_P y_Q - x_Q y_P)\int_{0}^{1}x_P u\left[v\right]_{v = 0}^{v = 1-u} + \frac{x_Q}{2}\left[v^2\right]_{v = 0}^{v = 1-u}du \\ &= \frac{\rho}{m}(x_P y_Q - x_Q y_P)\int_{0}^{1} x_P u(1 - u) + \frac{x_Q}{2}(1 - u)^2 du \\ &= \frac{\rho}{m}(x_P y_Q - x_Q y_P) \left(\frac{x_P}{2} \left[u^2\right]_{0}^{1} - \frac{x_P}{3}\left[u^3\right]_{0}^{1} + \frac{x_Q}{2}\left[u\right]_{0}^{1} - \frac{x_Q}{2}\left[u^2\right]_{0}^{1} + \frac{x_Q}{6}\left[u^3\right]_{0}^{1}\right) \\ &= \frac{\rho}{m}(x_P y_Q - x_Q y_P) \left(\frac{x_P}{2} - \frac{x_P}{3} + \frac{x_Q}{2} - \frac{x_Q}{2} + \frac{x_Q}{6}\right) \\ &= \frac{\rho}{m}(x_P y_Q - x_Q y_P) \left(\frac{x_P + x_Q}{6}\right) \end{aligned} $$

The total mass of the plate is $ m = ho A = rac{1}{2} ho x_P y_Q $, and with the chosen configuration $y_P = 0$. Thus:

$$ x_C = rac{x_P + x_Q}{3} $$

Elliptical plate: center of mass #rcm-ee

$$ \vec{r}_C = \frac{2a\sin\theta}{3\theta}\hat{\imath} + \frac{2b\left(1 - \cos\theta\right)}{3\theta}\hat{\jmath} $$

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iiint_\mathcal{B} \rho \vec{r} \, dV \\ &= \frac{1}{m}\iint_{A} \rho \vec{r} \, dA \\ \end{aligned} $$

It is convenient to switch to cylindrical coordinates:

$$ \begin{aligned} x &= a \, r \cos\theta \\ y &= b \, r \sin\theta \\ \end{aligned} $$

The Jacobian of this coordinate transformation is:

$$ \begin{aligned} J &= \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{vmatrix} = \begin{vmatrix} a\cos\theta & -a r \sin\theta \\ b \sin\theta & b r\cos\theta \end{vmatrix} = a b r \cos^2\theta + a b r\sin^2\theta = a b r \\ \end{aligned} $$

Therefore:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iint_{A} \rho \vec{r} \, dx \, dy \\ &= \frac{\rho}{m}\int_{0}^{\theta} \int_{0}^{1} \left[ar\cos\theta\hat{\imath} + br\sin\theta\hat{\jmath}\right] \, J \, dr \, d\theta \\ &= \frac{\rho ab}{m}\int_{0}^{\theta} \int_{0}^{1} \left[ar^2\cos\theta\hat{\imath} + br^2\sin\theta\hat{\jmath}\right] \, dr \, d\theta \\ &= \frac{\rho ab}{m}\int_{0}^{\theta} \left[\frac{r^3}{3}\right]_{0}^{1}a\cos\theta\hat{\imath} + \left[\frac{r^3}{3}\right]_{0}^{1}b\sin\theta\hat{\jmath} \, d\theta \\ &= \frac{\rho ab}{m}\int_{0}^{\theta} \left[\frac{1}{3}a\cos\theta\hat{\imath} + \frac{1}{3}b\sin\theta\hat{\jmath}\right] \, d\theta \\ &= \frac{\rho ab}{m}\left(\left[\sin\theta\right]_{0}^{\theta}\frac{1}{3}a\hat{\imath} + \left[-\cos\theta\right]_{0}^{\theta}\frac{1}{3}b\hat{\jmath}\right) \\ &= \frac{\rho ab}{m}\left[\frac{1}{3}a\sin\theta\hat{\imath} + \frac{1}{3}b\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ \end{aligned} $$

The total mass of the sector is $ m = \rho A = \frac{\theta}{2}\rho ab $. Thus:

$$ \begin{aligned} \vec{r}_C &= \frac{\rho ab}{m}\left[\frac{1}{3}a\sin\theta\hat{\imath} + \frac{1}{3}b\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ &= \frac{\rho ab}{\frac{\theta}{2}\rho ab}\left[\frac{1}{3}a\sin\theta\hat{\imath} + \frac{1}{3}b\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ &= \frac{2}{\theta}\left[\frac{1}{3}a\sin\theta\hat{\imath} + \frac{1}{3}b\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ &= \frac{2a\sin\theta}{3\theta}\hat{\imath} + \frac{2b\left(1 - \cos\theta\right)}{3\theta}\hat{\jmath} \end{aligned} $$

Simplified shapes

The centers of mass listed below are all special cases of the basic shapes given in Section #rcm-bs. Other special cases can be easily obtained by similar methods, or directly computing the integral.

Right triangular plate: center of mass #rcm-eg

$$ \vec{r}_C = \frac{b}{3}\hat{\imath} + \frac{h}{3}\hat{\jmath} $$

See example problem on how to derive it by directly computing the integrals.

The other perhaps simpler approach is to let $x_Q = 0$ in #rcm-et, which forms a right triangle if the configuration is the same as the one shown in the figure. Thus:

$$ \begin{aligned} \vec{r}_C &= \frac{x_P + x_Q}{3}\hat{\imath} + \frac{y_Q}{3}\hat{\jmath} \\ &= \frac{x_P}{3}\hat{\imath} + \frac{y_Q}{3}\hat{\jmath} \\ &= \frac{b}{3}\hat{\imath} + \frac{h}{3}\hat{\jmath} \end{aligned} $$

Isosceles triangular plate: center of mass #rcm-ei

$$ \vec{r}_C = \frac{b}{2}\hat{\imath} + \frac{h}{3}\hat{\jmath} $$

See example problem on how to derive it by directly computing the integrals.

The other perhaps simpler approach is to let $x_Q = 0$ in #rcm-et, which forms a right triangle if the configuration is the same as the one shown in the figure. Thus:

$$ \begin{aligned} \vec{r}_C &= \frac{x_P + x_Q}{3}\hat{\imath} + \frac{y_Q}{3}\hat{\jmath} \\ &= \frac{x_P + \frac{x_P}{2}}{3}\hat{\imath} + \frac{y_Q}{3}\hat{\jmath} \\ &= \frac{\frac{3}{2}x_P}{3}\hat{\imath} + \frac{y_Q}{3}\hat{\jmath} \\ &= \frac{b}{2}\hat{\imath} + \frac{h}{3}\hat{\jmath} \end{aligned} $$

Circular sector: center of mass #rcm-ec

$$ \vec{r}_C = \frac{2r\sin\theta}{3\theta}\hat{\imath} + \frac{2r\left(1 - \cos\theta\right)}{3\theta}\hat{\jmath} $$

We could use the integral definition of the center of mass and compute it directly:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iiint_\mathcal{B} \rho \vec{r} \, dV \\ &= \frac{1}{m}\iint_{A} \rho \vec{r} \, dA \\ \end{aligned} $$

It is convenient to switch to cylindrical coordinates:

$$ \begin{aligned} x &= r \cos\theta \\ y &= r \sin\theta \\ \end{aligned} $$

The Jacobian of this coordinate transformation is:

$$ \begin{aligned} J &= \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{vmatrix} = \begin{vmatrix} \cos\theta & -r \sin\theta \\ \sin\theta & r\cos\theta \end{vmatrix} = r \cos^2\theta + r \sin^2\theta = r \end{aligned} $$

Therefore:

$$ \begin{aligned} \vec{r}_C &= \frac{1}{m}\iint_{A} \rho \vec{r} \, dx \, dy \\ &= \frac{\rho}{m}\int_{0}^{\theta} \int_{0}^{r} \left[r\cos\theta\hat{\imath} + r\sin\theta\hat{\jmath}\right] \, J \, dr \, d\theta \\ &= \frac{\rho}{m}\int_{0}^{\theta} \int_{0}^{r} \left[r^2\cos\theta\hat{\imath} + r^2\sin\theta\hat{\jmath}\right] \, dr \, d\theta \\ &= \frac{\rho}{m}\int_{0}^{\theta} \left[\frac{r^3}{3}\right]_{0}^{r}\cos\theta\hat{\imath} + \left[\frac{r^3}{3}\right]_{0}^{r}\sin\theta\hat{\jmath} \, d\theta \\ &= \frac{\rho}{m}\int_{0}^{\theta} \left[\frac{r^3}{3}\cos\theta\hat{\imath} + \frac{r^3}{3}\sin\theta\hat{\jmath}\right] \, d\theta \\ &= \frac{\rho}{m}\left(\left[\sin\theta\right]_{0}^{\theta}\frac{r^3}{3}\hat{\imath} + \left[-\cos\theta\right]_{0}^{\theta}\frac{r^3}{3}\hat{\jmath}\right) \\ &= \frac{\rho}{m}\left[\frac{1}{3}r^3\sin\theta\hat{\imath} + \frac{1}{3}r^3\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ \end{aligned} $$

The total mass of the sector is $ m = \rho A = \frac{\theta}{2}\rho r^2 $. Thus:

$$ \begin{aligned} \vec{r}_C &= \frac{\rho}{m}\left[\frac{1}{3}r^3\sin\theta\hat{\imath} + \frac{1}{3}r^3\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ &= \frac{\rho}{\frac{\theta}{2}\rho r^2}\left[\frac{1}{3}r^3\sin\theta\hat{\imath} + \frac{1}{3}r^3\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ &= \frac{2}{\theta r^2}\left[\frac{1}{3}r^3\sin\theta\hat{\imath} + \frac{1}{3}r^3\left(1 - \cos\theta\right)\hat{\jmath}\right] \\ &= \frac{2r\sin\theta}{3\theta}\hat{\imath} + \frac{2r\left(1 - \cos\theta\right)}{3\theta}\hat{\jmath} \end{aligned} $$

Another way to reach this formula is to use #rcm-ee, and for a circular sector, let $a = b = r$.

Semi-circular sector: center of mass #rcm-es

$$ \vec{r}_C = \frac{4r}{3\pi}\hat{\jmath} $$

Using #rcm-ec, for a semi-circular sector, the angle $ \theta = \pi $. Therefore:

$$ \begin{aligned} \vec{r}_C &= \frac{2r\sin\theta}{3\theta}\hat{\imath} + \frac{2r\left(1 - \cos\theta\right)}{3\theta}\hat{\jmath} \\ &= \frac{2r\sin(\pi)}{3\pi}\hat{\imath} + \frac{2r\left(1 - \cos(\pi)\right)}{3\pi}\hat{\jmath} \\ &= 0 + \frac{4r}{3\pi}\hat{\jmath} \\ &= \frac{4r}{3\pi}\hat{\jmath} \end{aligned} $$

Moment of Inertia

The moment of inertia of a body, written $ I_{P,\hat{a}} $, is measured about a rotation axis through point $P$ in direction $ \hat{a} $. The moment of inertia expresses how hard it is to produce an angular acceleration of the body about this axis. That is, a body with high moment of inertia resists angular acceleration, so if it is not rotating then it is hard to start a rotation, while if it is already rotating then it is hard to stop.

The moment of inertia plays the same role for rotational motion as the mass does for translational motion (a high-mass body resists is hard to start moving and hard to stop again).

Moment of inertia about axis $ \hat{a} $ through point (P). #rem-ei

$$ \begin{gathered} I_{P,\hat{a}} = \iiint_\mathcal{B} \rho r^2 \,dV \\ \text{(units: $\rm kg\ m^2$)} \end{gathered} $$

The distance $r $ is the perpendicular distance to $ dV $ from the axis through $P$ in direction $ \hat{a}. $

Warning: Mass moments of inertia are different to area moments of inertia. #rem-wm

Be advised that the "moment of inertia" encountered in Statics is not the same as the moment of inertia used in Dynamics. Strictly speaking, the "moment of inertia" from Statics shouldn't even be called "moment of inertia." What it really is is the "second moment of area." Below are the definitions of two such second moments of area:

$$ J_{xx}=\iint_{A}{y^{2}dA} $$

$$ J_{yy}=\iint_{A}{x^{2}dA} $$

In contrast, the moment of inertia (about the $z$-axis) is defined as stated above.

For example, a rectangle of base $b$ and height $h$ has the following moments about its centroid $C$:

$$ J^{C}_{xx}=\frac{1}{12}bh^{3} $$

$$ J^{C}_{yy}=\frac{1}{12}b^{3}h $$

$$ I^{C}_{zz}=\frac{1}{12}m(b^{2}+h^{2}) $$

Notice that the dimensions of the two quantities are different. While the dimension of second moment of area is $ (\text{length})^{4} $, the dimension of moment of inertia is $ (\text{mass})(\text{length})^{2} $. When doing dynamics problems with moments of inertia, you should not use the formulas you remember for second moment of area instead. You will get the wrong answer!

Observe that the moment of inertia is proportional to the mass, so that doubling the mass of an object will also double its moment of inertia. In addition, the moment of inertia is proportional to the square of the size of the object, so that doubling every dimension of an object (height, width, etc) will cause it to have four times the moment of inertia.

Moments of inertia about coordinate axes through point (P). #rem-ec

$$ \begin{aligned} I_{P,x} &= I_{P,xx} = I_{P,\hat\imath} = \iiint_\mathcal{B} \rho (y^2 + z^2) \,dx\,dy\,dz \\ I_{P,y} &= I_{P,yy} = I_{P,\hat\jmath} = \iiint_\mathcal{B} \rho (z^2 + x^2) \,dx\,dy\,dz \\ I_{P,z} &= I_{P,zz} = I_{P,\hat{k}} = \iiint_\mathcal{B} \rho (x^2 + y^2) \,dx\,dy\,dz \end{aligned} $$

The coordinates $(x,y,z)$ in the body are measured from point $P$.

The distance$r$ in the moment of inertia integral #rem-ei is the perpendicular distance from the axis of rotation to the infinitesimal volume $dV $. If we are using rectangular coordinates $(x,y,z)$ measured from point $P$, and the axis of rotation is one of the coordinate axes, then the perpendicular distance is very simple.

As an example, consider the case when the axis of rotation $ \hat{a} $ is the $ \hat{k} $ axis, as shown in the figure. Then the perpendicular distance $r$ satisfies $r^2 = x^2 + y^2$, giving the coordinate expression above. The other two coordinate axes are similar.

Example Problem: Moment of inertia of a square plate. #rem-xs

A solid square uniform plate has mass $m$, side-length $ \ell $, and thickness $ h $. What is the moment of inertia about the $z $-axis through the center of mass $C$?

We will use the coordinate formula #rem-ec. To do this, we measure the position from the point $C$ about which we are computing the moment of inertia, so the coordinate origin is at $C$. The figure to the right shows the 3D configuration of the body, where we see that the $x$-coordinate range of the body is $-\ell/2$ to $\ell/2$, and the same for the $y$-coordinate, while the $z$-coordinate ranges from $-h/2$ to $h/2$.

Taking the density of the plate to be $\rho$, we thus have:

$$ \begin{aligned} I_{C,z} &= \iiint_\mathcal{B} \rho (x^2 + y^2) \,dx\,dy\,dz \\ &= \int_{-h/2}^{h/2} \int_{-\ell/2}^{\ell/2} \int_{-\ell/2}^{\ell/2} \rho (x^2 + y^2) \,dx\,dy\,dz \\ &= \int_{-h/2}^{h/2} \int_{-\ell/2}^{\ell/2} \left[ \rho \left(\frac{1}{3}x^3 + y^2 x\right)\right]_{x = -\ell/2}^{x = \ell/2} \,dy\,dz \\ &= \int_{-h/2}^{h/2} \int_{-\ell/2}^{\ell/2} \rho \left(\frac{1}{12}\ell^3 + y^2 \ell \right) \,dy\,dz \\ &= \int_{-h/2}^{h/2} \left[ \rho \left(\frac{1}{12}\ell^3 y + \frac{1}{3} y^3 \ell \right) \right]_{y = -\ell/2}^{y = \ell/2} \,dz \\ &= \int_{-h/2}^{h/2} \rho \left(\frac{1}{12}\ell^4 + \frac{1}{12} \ell^4 \right) \,dz \\ &= \int_{-h/2}^{h/2} \rho \frac{1}{6}\ell^4 \,dz \\ &= \left[ \rho \frac{1}{6}\ell^4 z \right]_{z = -h/2}^{z = h/2} \\ &= \rho \frac{1}{6}\ell^4 h. \end{aligned} $$

The total mass of the plate is $ m = \rho \ell^2 h $, so we can write the moment of inertia as $ I_{C,z} = \frac{1}{6} m \ell^2. $ The square plate moment of inertia is actually a special case of the rectangular prism formula #rem-er with $ \ell_y = \ell_z = \ell $

Did you know?

We are always considering the moment of inertia to be a scalar value $ I $, which is valid for rotation about a fixed axis. For more complicated dynamics with tumbling motion about multiple axes simultaneously, it is necessary to consider the full 3 × 3 moment of inertia matrix:

$$ I = \begin{bmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{bmatrix} $$

The three scalar moments of inertia from #rem-ec appear on the diagonal. The off-diagonal terms are called the products of inertia and are given by

$$ I_{xy} = -\iiint_{\mathcal{B}} \rho xy \,dx\,dy\,dz, $$

and similarly for the other terms. The angular momentum of a rigid body is given by $ \vec{H} = I \vec{\omega} $, which is the matrix product of the moment of inertia matrix with the angular velocity vector. This is important in advanced dynamics applications such as unbalanced rotating shafts and the precession of gyroscopes.

Parallel axis theorem

Parallel axis theorem. #rem-el

$$ I_{P,\hat{a}} = I_{C,\hat{a}} + m \, d^2 $$

Here $ d $ is the perpendicular distance between the axes through $ P $ and $C $ in direction $ \hat{a} $, so $ d = \| \operatorname*{Comp}(\vec{r}_{CP}, \hat{a})\| $.

To easily compute the moments of inertia relative to axes through $ P $ and $ C $ it is easiest to choose a coordinate system aligned with the rotation axis direction $ \hat{a} $. We will choose coordinates $ (x,y,z) $ measured from the center of mass $ C $ and with the $z$-axis $ \hat{k} $ in the direction of $ \hat{a} $, as shown in the figure.

As we integrate over the body with infinitesimal volume $ dV $ at position $ (x,y,z) $ from $ C $, we will write the distance from the axis through $ C $ as $ r_c $ and the distance from the axis through $ P $ as $ r_P $, as illustrated. The distance between the two rotation axes is $ d $. In the chosen coordinate system this means that:

$$ \begin{aligned} {r_C}^2 &= x^2 + y^2 \\ {r_P}^2 &= (x - x_P)^2 + (y - y_P)^2 \\ d^2 &= {x_P}^2 + {y_P}^2, \end{aligned} $$

where $ P $ has position $ (x_P, y_P, z_P) $ in these coordinates.

Computing the integral #rem-ec to find the moment of inertia about the axis through $ P $ in direction $ \hat{a} $ now gives:

$$ \begin{aligned} I_{P,\hat{a}} &= \int_{\mathcal{B}} \rho {r_P}^2 \,dV \\ &= \iiint_{\mathcal{B}} \rho \left((x - x_P)^2 + (y - y_P)^2\right) \,dx\,dy\,dz \\ &= \iiint_{\mathcal{B}} \rho \left(x^2 - 2 x x_P + {x_P}^2 + y^2 - 2 y y_P + {y_P}^2\right) \,dx\,dy\,dz \\ &= \iiint_{\mathcal{B}} \rho (x^2 + y^2) \,dx\,dy\,dz - 2 x_P \iiint_{\mathcal{B}} \rho x \,dx\,dy\,dz \\ &\quad - 2 y_P \iiint_{\mathcal{B}} \rho y \,dx\,dy\,dz + ({x_P}^2 + {y_P}^2) \iiint_{\mathcal{B}} \rho \,dx\,dy\,dz \\ &= \int_{\mathcal{B}} \rho {r_C}^2 \,dV + d^2 \int_{\mathcal{B}} \rho \,dV \\ &= I_{C,\hat{a}} + m d^2. \end{aligned} $$

Here we used the coordinate representation of the center of mass to realize that the $ x $ coordinate of $ C $ is $ x_C = \frac{1}{m} \int_{\mathcal{B}} \rho x \,dV $, but because our coordinates are measured from $ C $ we must have $ x_C = 0 $ and so $ \int_{\mathcal{B}} \rho x \,dV = 0 $. The integral of $ \rho y $ is similarly zero.

Warning: Parallel axis theorem must start from center of mass $ C $. #rem-wl

The parallel axis theorem does not apply to any two parallel rotation axes. The rotation axis on the right-hand-side of the equation must be through the center of mass $ C $, although the other axis can be through any point $ P $.

Warning: Parallel axis theorem $ d $ is perpendicular distance, not $ r_{CP} $. #rem-wp

The distance $ d $ in the parallel axis theorem is the perpendicular distance between the axes through points $ P $ and $ C $. This will normally not be the same as the distance $ r_{CP} $ between $ P $ and $ C $, except in 2D problems or if it happens that $ \vec{r}_{CP} $ is already perpendicular to the rotation axis $ \hat{a} $. The distance $ d $ can be computed by taking the orthogonal complement of $ \vec{r}_{CP} $ with respect to $ \hat{a} $, so $ d = \|\operatorname{Comp}(\vec{r}_{CP}, \hat{a})\| $.

Example Problem: Moment of inertia of a square plate about a corner. #rem-xc

A solid uniform square plate has mass $ m $, side-length $ \ell $, and thickness $ h $. What is the moment of inertia about the $ z $-axis through the corner $ P $?

Use the answer to Example Problem #rem-xs and the parallel axis theorem #rem-el.

In Example Problem #rem-xs we computed the moment of inertia of a square place about the center to be $ I_{C,z} = \frac{1}{6} m \ell^2 $. The parallel axis theorem #rem-el now gives:

$$ \begin{aligned} I_{P,z} &= I_{C,z} + m \, {r_{CP}}^2 \\ &= \frac{1}{6} m \ell^2 + m \left( \left(\frac{\ell}{2}\right)^2 + \left(\frac{\ell}{2}\right)^2 \right) \\ &= \frac{2}{3} m \ell^2. \end{aligned} $$

To check our answer, we can compute the corner moment of inertia directly by integrating with formula #rem-ec. To do this, we put the coordinate origin at the point $ P $ about which we wish to find the moment of inertia, as shown in 3D to the right. From this we see that the $x $range is $0$ to $ \ell $, the same for the $ y $ range, and the $z$ range is $-h/2$ to $h/2$.

The integral formula now gives:

$$ \begin{aligned} I_{P,z} &= \iiint_\mathcal{B} \rho (x^2 + y^2) \,dx\,dy\,dz \\ &= \int_{-h/2}^{h/2} \int_0^{\ell} \int_{0}^{\ell} \rho (x^2 + y^2) \,dx\,dy\,dz \\ &= \int_{-h/2}^{h/2} \int_{0}^{\ell} \left[ \rho \left(\frac{1}{3}x^3 + y^2 x\right)\right]_{x = 0}^{x = \ell} \,dy\,dz \\ &= \int_{-h/2}^{h/2} \int_{0}^{\ell} \rho \left(\frac{1}{3}\ell^3 + y^2 \ell \right) \,dy\,dz \\ &= \int_{-h/2}^{h/2} \left[ \rho \left(\frac{1}{3}\ell^3 y + \frac{1}{3} y^3 \ell \right) \right]_{y = 0}^{y = \ell} \,dz \\ &= \int_{-h/2}^{h/2} \rho \left(\frac{1}{3}\ell^4 + \frac{1}{3} \ell^4 \right) \,dz \\ &= \int_{-h/2}^{h/2} \rho \frac{2}{3}\ell^4 \,dz \\ &= \left[ \rho \frac{2}{3}\ell^4 z \right]_{z = -h/2}^{z = h/2} \\ &= \rho \frac{2}{3}\ell^4 h. \end{aligned} $$

The total mass of the plate is $ m = \rho ell^2 h $, so we can write the final expression for the moment of inertia is

$$ I_{P,z} = \frac{2}{3} m \ell^2. $$

This is the same as the expression we obtained above using the parallel axis theorem, but clearly the parallel axis theorem version is much easier.

One consequence of the parallel axis theorem is that the moment of inertia can only increase as we move the rotation point $ P $ away from the center of mass $ C $. This means that the point with the lowest moment of inertia is always the center of mass itself.

A second consequence of the parallel axis theorem is that moving the point $ P $ along the direction $ \hat{a} $ doesn't change the moment of inertia, because the axis of rotation is not changing as the point moves along the axis itself.

Additive theorem

Adding moments of inertia. #rem-ea

$$ I^{\mathcal{B}}_{P,\hat{a}} = I^{\mathcal{B}_1}_{P,\hat{a}} + I^{\mathcal{B}_2}_{P,\hat{a}} $$

The whole body $ \mathcal{B} $ is composed of sub-bodies $ \mathcal{B}_1 $ and $ \mathcal{B}_2 $.

The addition of moments of inertia for sub-bodies to give the full moment of inertia follows directly from the fact that the integral over the whole body is the sum of the integrals over the sub-bodes. That is, for $ \mathcal{B} = \mathcal{B}_1 \cup \mathcal{B}_2 $ (and $ \mathcal{B}_1 $ not overlapping with $ \mathcal{B}_2 $), we have:

$$ \begin{aligned} I^{\mathcal{B}}_{P,\hat{a}} &= \int_{\mathcal{B}} \rho r^2 \,dV \\ &= \int_{\mathcal{B_1} \cup \mathcal{B}_2} \rho r^2 \,dV \\ &= \int_{\mathcal{B_1}} \rho r^2 \,dV + \int_{\mathcal{B}_2} \rho r^2 \,dV \\ &= I^{\mathcal{B}_1}_{P,\hat{a}} + I^{\mathcal{B}_2}_{P,\hat{a}}. \end{aligned} $$

Warning: To add moments of inertia they must be about the same axis. #rem-wa

It is only valid to add together moments of inertia for different sub-bodies if each moment of inertia is computed about the same axis of rotation. For example, consider $ I^{\mathcal{B}_1}_{C_1,z} $ and $ I^{\mathcal{B}_2}_{C_2,z} $, which are the moments of inertia of bodies $ \mathcal{B}_1 $ and $ \mathcal{B}_2 $ about each of their individual centers of mass $ C_1 $ and $ C_2 $ (with axis direction $ z $). Now it is physically meaningless to form the sum $ I^{\mathcal{B}_1}_{C_1,z} + I^{\mathcal{B}_2}_{C_2,z} $, because each moment of inertia is about a different axis. We must first shift both moments of inertia to a common axis point $ P $ (perhaps by using the parallel axis theorem), and then we can meaningfully add them together.

Example Problem: Moment of inertia of an L-shaped plate. #rem-xl

A solid uniform L-shaped plate has mass $m$ and dimensions as shown. What is the moment of inertia about the $z$-axis through the corner $P$?

Recall that in Example Problem #rem-xs we computed the moment of inertia of a square place about the center to be $ I_{C,z} = \frac{1}{6} m \ell^2 $.

To use this together with the parallel axis theorem #rem-el and the additive theorem #rem-ea, we must first realize that the L-shape can be decomposed into four square plates, as shown. Each small square body has the same mass and the same moment of inertia about its center, so:

$$ \begin{aligned} m_1 &= \frac{1}{4} m \\ I^{\mathcal{B}_1}_{C_1,z} &= \frac{1}{6} m_1 (2d)^2 = \frac{1}{6} \left(\frac{1}{4} m\right) 4d^2 = \frac{1}{6} m d^2, \end{aligned} $$

and similarly for each other small square body.

Now individual moments of inertia about the corner $P$ can be found using the parallel axis theorem:

$$ \begin{aligned} I^{\mathcal{B}_1}_{P,z} &= I^{\mathcal{B}_1}_{C_1,z} + m_1 \, {r_{C_1P}}^2 = \frac{1}{6} m d^2 + \left(\frac{1}{4} m\right) \left(d^2 + (3d)^2\right) = \frac{8}{3} m d^2 \\ I^{\mathcal{B}_2}_{P,z} &= I^{\mathcal{B}_2}_{C_2,z} + m_2 \, {r_{C_2P}}^2 = \frac{1}{6} m d^2 + \left(\frac{1}{4} m\right) \left(d^2 + d^2\right) = \frac{2}{3} m d^2 \\ I^{\mathcal{B}_3}_{P,z} &= I^{\mathcal{B}_1}_{P,z} = \frac{8}{3} m d^2 \\ I^{\mathcal{B}_4}_{P,z} &= I^{\mathcal{B}_4}_{C_4,z} + m_4 \, {r_{C_4P}}^2 = \frac{1}{6} m d^2 + \left(\frac{1}{4} m\right) \left((5d)^2 + d^2\right) = \frac{20}{3} m d^2. \end{aligned} $$

Here we observed that body $ \mathcal{B}_3 $ will have the same moment of inertia as $ \mathcal{B}_1 $ , saving some computation.

Combining the individual moments of inertia now gives us the total:

$$ \begin{aligned} I_{P,z} &= I^{\mathcal{B}_1}_{P,z} + I^{\mathcal{B}_2}_{P,z} + I^{\mathcal{B}_3}_{P,z} + I^{\mathcal{B}_4}_{P,z} \\ &= \frac{8}{3} m d^2 + \frac{2}{3} m d^2 + \frac{8}{3} m d^2 + \frac{20}{3} m d^2\\ &= \frac{38}{3} m d^2. \end{aligned} $$

We could also directly compute the total moment of inertia using the integral formula #rem-ec, which would be quite complex.

Basic shapes

The moments of inertia listed below are all computed directly from the integrals #rem-ec.

Point mass: moments of inertia #rem-ep

$$ I_{P,z} = m r^2 $$

Rectangular prism: moments of inertia #rem-er

$$ \begin{aligned}I_{C,x}&=\frac{1}{12}m({\ell_y}^2+{\ell_z}^2)\\I_{C,y}&=\frac{1}{12}m({\ell_z}^2+{\ell_x}^2)\\I_{C,z}&=\frac{1}{12}m({\ell_x}^2+{\ell_y}^2)\end{aligned} $$

The calculation for any of the axes is the same, so we will only write out the derivation of $ I_{C,z} $ here. We use #rem-ec, which gives:

$$ \begin{aligned} I_{C,z} &= \iiint_\mathcal{B} \rho (x^2 + y^2) \,dx\,dy\,dz \\ &= \int_{-\ell_z/2}^{\ell_z/2} \int_{-\ell_y/2}^{\ell_y/2} \int_{-\ell_x/2}^{\ell_x/2} \rho (x^2 + y^2) \,dx\,dy\,dz \\ &= \int_{-\ell_z/2}^{\ell_z/2} \int_{-\ell_y/2}^{\ell_y/2} \left[ \rho \left(\frac{1}{3}x^3 + y^2 x\right)\right]_{x = -\ell_x/2}^{x = \ell_x/2} \,dy\,dz \\ &= \int_{-\ell_z/2}^{\ell_z/2} \int_{-\ell_y/2}^{\ell_y/2} \rho \left(\frac{1}{12}{\ell_x}^3 + y^2 \ell_x \right) \,dy\,dz \\ &= \int_{-\ell_z/2}^{\ell_z/2} \left[ \rho \left(\frac{1}{12}{\ell_x}^3 y + \frac{1}{3} y^3 \ell_x \right) \right]_{y = -\ell_y/2}^{y = \ell_y/2} \,dz \\ &= \int_{-\ell_z/2}^{\ell_z/2} \rho \left(\frac{1}{12}{\ell_x}^3 \ell_y + \frac{1}{12} \ell_x {\ell_y}^3 \right) \,dz \\ &= \int_{-\ell_z/2}^{\ell_z/2} \rho \ell_x \ell_y \frac{1}{12}\left( {\ell_x}^2 + {\ell_y}^2\right) \,dz \\ &= \left[ \rho \ell_x \ell_y \frac{1}{12}\left( {\ell_x}^2 + {\ell_y}^2\right) z \right]_{z = -\ell_z/2}^{z = \ell_z/2} \\ &= \rho \ell_x \ell_y \ell_z \frac{1}{12}\left( {\ell_x}^2 + {\ell_y}^2\right). \end{aligned} $$

The total mass of the plate is $ m=\rho\ell_x\ell_y\ell_z $, so we can write the moment of inertia as

$$ I_{C,z}=\frac{1}{12}m\left({\ell_x}^2+{\ell_y}^2\right).\ $$

Cylindrical thick shell: moments of inertia #rem-ey

$$ \begin{aligned}I_{C,x}&=I_{C,y}=\frac{1}{12}m(3({r_1}^2+{r_2}^2)+\ell^2)\\I_{C,z}&=\frac{1}{2}m({r_1}^2+{r_2}^2)\end{aligned} $$

To compute the integrals in #rem-ec it is convenient to switch to cylindrical coordinates:

$$ \begin{aligned}x &= r \cos\theta \\y &= r \sin\theta \\z &= z.\end{aligned}\ $$

The Jacobian of this coordinate transformation is:

$$ \begin{aligned}J &= \begin{vmatrix}\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\\frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}\end{vmatrix}= \begin{vmatrix}\cos\theta & -r \sin\theta & 0 \\\sin\theta & r \cos\theta & 0 \\0 & 0 & 1\end{vmatrix}= r \cos^2\theta + r \sin^2\theta= r.\end{aligned}\ $$

Starting with the $ z $ axis, the moment of inertia is thus:

$$ \begin{aligned}I_{C,z} &= \iiint_\mathcal{B} \rho (x^2 + y^2) \,dx\,dy\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \int_{r_1}^{r_2}\rho \left( (r \cos\theta)^2 + (r \sin\theta)^2 \right) \,J \,dr\,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \int_{r_1}^{r_2}\rho r^3 \,dr\,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \left[\rho \frac{1}{4} r^4 \right]_{r = r_1}^{r = r_2} \,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \frac{1}{4} \rho \left({r_2}^4 - {r_1}^4 \right) \,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \left[ \frac{1}{4} \rho \left({r_2}^4 - {r_1}^4 \right) \theta \right]_{\theta = 0}^{\theta = 2\pi} \,dz \\&= \int_{-\ell/2}^{\ell/2} \frac{\pi}{2} \rho \left({r_2}^4 - {r_1}^4 \right) \,dz \\&= \left[ \frac{\pi}{2} \rho \left({r_2}^4 - {r_1}^4 \right) z \right]_{z = -\ell/2}^{z = \ell/2} \\&= \frac{\pi}{2} \rho \ell \left({r_2}^4 - {r_1}^4 \right).\end{aligned} $$

The total mass of the cylindrical shell is $ m = \rho(\pi {r_2}^2 - \pi {r_1}^2) \ell $ , so we can write the moment of inertia as

$$ \begin{aligned}I_{C,z}&= \frac{1}{2} \frac{m}{{r_2}^2 - {r_1}^2}\left( {r_2}^4 - {r_1}^4 \right) \\&= \frac{1}{2} \frac{m}{{r_2}^2 - {r_1}^2}\left( {r_2}^2 + {r_1}^2 \right) \left( {r_2}^2 - {r_1}^2 \right) \\&= \frac{1}{2} m\left( {r_2}^2 + {r_1}^2 \right).\end{aligned}\ $$

Due to rotational symmetry of the cylinder, the moment of inertia will be the same about any axis orthogonal to $ z $ , so we will just write out the derivation for $ I_{C,x} $ here. We again use #rem-ec in cylindrical coordinates, giving:

$$ \begin{aligned}I_{C,x} &= \iiint_\mathcal{B} \rho (y^2 + z^2) \,dx\,dy\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \int_{r_1}^{r_2}\rho \left( (r \sin\theta)^2 + z^2 \right) \,J \,dr\,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \int_{r_1}^{r_2}\rho \left( r^3 \sin^2\theta + r z^2 \right) \,dr\,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi} \left[\rho \left( \frac{1}{4} r^4 \sin^2\theta + \frac{1}{2} r^2 z^2 \right)\right]_{r = r_1}^{r = r_2} \,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi}\rho \left( \frac{1}{4} ({r_2}^4 - {r_1}^4) \sin^2\theta+ \frac{1}{2} ({r_2}^2 - {r_1}^2) z^2 \right) \,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \int_0^{2\pi}\rho \left( \frac{1}{8} ({r_2}^4 - {r_1}^4) (1 - \cos 2\theta)+ \frac{1}{2} ({r_2}^2 - {r_1}^2) z^2 \right) \,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \left[\rho \left( \frac{1}{8} ({r_2}^4 - {r_1}^4)\left(\theta - \frac{1}{2} \sin 2\theta\right)+ \frac{1}{2} ({r_2}^2 - {r_1}^2) z^2 \theta \right)\right]_{\theta = 0}^{\theta = 2\pi} \,d\theta\,dz \\&= \int_{-\ell/2}^{\ell/2} \rho \left( \frac{\pi}{4} ({r_2}^4 - {r_1}^4)+ \pi ({r_2}^2 - {r_1}^2) z^2 \right) \,d\theta\,dz \\&= \left[ \rho \left( \frac{\pi}{4} ({r_2}^4 - {r_1}^4) z+ \pi ({r_2}^2 - {r_1}^2) \frac{1}{3} z^3 \right) \right]_{z = -\ell/2}^{z = \ell/2} \\&= \rho \left( \frac{\pi}{4} ({r_2}^3 - {r_1}^3) \ell+ \pi ({r_2}^2 - {r_1}^2) \frac{1}{12} \ell^3 \right) \\&= \frac{1}{12} \rho \pi ({r_2}^2 - {r_1}^2) \ell \left( 3 ({r_2}^2 + {r_1}^2)+ \ell^2 \right).\end{aligned} $$

In the last line we again used the factorization $ ({r_2}^4 - {r_1}^4) = ({r_2}^2 + {r_1}^2) ({r_2}^2 -{r_1}^2) $ . Now we can substitute in the total mass $ m =\rho \pi ({r_2}^2 - {r_1}^2) \ell $ to obtain:

$$ \begin{aligned}I_{C,x}&= \frac{1}{12} m \left( 3 ({r_2}^2 + {r_1}^2)+ \ell^2 \right).\end{aligned} $$

Spherical thick shell: moments of inertia #rem-es

$$ \begin{aligned}I_C&=\frac{2}{5}m\left(\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right)\end{aligned} $$

To compute the integrals in #rem-ec it is convenient to switch to spherical coordinates:

$$ \begin{aligned}x &= r \cos\theta \sin\phi \\y &= r \sin\theta \sin\phi \\z &= r \cos\phi.\end{aligned}\ $$

To find the Jacobian of this coordinate transformation we use the coordinate order $ (r,\phi,\theta) $ to give a right-handed spherical system. Then: Due to spherical symmetry, all axes through $ C $ will have the same moment of inertia. We will compute $ I_{C,z} $ , which is:

$$ \begin{aligned}I_{C,z} &= \iiint_\mathcal{B} \rho (x^2 + y^2) \,dx\,dy\,dz \\&= \int_0^{\pi} \int_{-\pi}^{\pi} \int_{r_1}^{r_2}\rho \left( (r \cos\theta \sin\phi)^2 + (r \sin\theta \sin\phi)^2 \right) \,J \,dr\,d\theta\,d\phi \\&= \int_0^{\pi} \int_{-\pi}^{\pi} \int_{r_1}^{r_2}\rho r^4 \sin^3\phi \,dr\,d\theta\,d\phi \\&= \int_0^{\pi} \int_{-\pi}^{\pi} \left[\rho \frac{1}{5} r^5 \sin^3\phi \right]_{r = r_1}^{r = r_2} \,d\theta\,d\phi \\&= \int_0^{\pi} \int_{-\pi}^{\pi}\rho \frac{1}{5} ({r_2}^5 - {r_1}^5) \sin^3\phi \,d\theta\,d\phi \\&= \int_0^{\pi} \left[\rho \frac{1}{5} ({r_2}^5 - {r_1}^5) \sin^3\phi \, \theta\right]_{\theta = -\pi}^{\theta = \pi} \,d\phi \\&= \int_0^{\pi}\rho \frac{2\pi}{5} ({r_2}^5 - {r_1}^5) \sin^3\phi \,d\phi \\&= \int_0^{\pi}\rho \frac{2\pi}{5} ({r_2}^5 - {r_1}^5) \frac{1}{4} (3\sin\phi - \sin 3\phi) \,d\phi \\&= \left[ \rho \frac{2\pi}{5} ({r_2}^5 - {r_1}^5) \frac{1}{4}\left(\frac{1}{3} \cos 3\phi - 3\cos\phi\right) \right]_{\phi = 0}^{\phi = \pi} \\&= \rho \frac{2\pi}{5} ({r_2}^5 - {r_1}^5) \frac{1}{4}\left(-\frac{2}{3} + 6\right) \\&= \frac{8}{15} \rho \pi ({r_2}^5 - {r_1}^5).\end{aligned} $$

The total mass of the spherical shell is $ m = \rho\left(\frac{4}{3} \pi {r_2}^3 - \frac{4}{3} \pi{r_1}^3\right) $ , so we can write the moment of inertia as

$$ \begin{aligned}I_{C,z}&= \frac{8}{15} m \frac{3}{4} \frac{1}{{r_2}^3 - {r_1}^3} ({r_2}^5 - {r_1}^5) \\&= \frac{2}{5} m \left(\frac{{r_2}^5 - {r_1}^5}{{r_2}^3 - {r_1}^3}\right).\end{aligned}\ $$

Simplified shapes

The moments of inertia listed below are all special cases of the basic shapes given in Section #rem-sb. Other special cases can be easily obtained by similar methods.

Rod: moments of inertia #rem-eo

$$ \begin{aligned}I_{C,z}&=\frac{1}{12}m\ell^2\\I_{P,z}&=\frac{1}{3}m\ell^2\\I_{C,x}&=I_{P,x}=0\end{aligned} $$

A rod is assumed to be a shape with infinitesimally small cross-section. We can use the formula #rem-ey for a cylinder with zero radii $ r_1 = r_2 = 0 $ . The coordinates here are set up so that $ z $ is orthogonal to the rod axis and $ x $ is along the axis, so #rem-ey gives:

$$ \begin{aligned}I_{C,z} &= \frac{1}{12} m (3({r_1}^2 + {r_2}^2) + \ell^2)= \frac{1}{12} m \ell^2 \\I_{C,x} &= \frac{1}{2} m ({r_1}^2 + {r_2}^2) = 0.\end{aligned}\ $$

To find the moment of inertia about the end point $ P $ we can use the parallel axis theorem #rem-el. This results is:

$$ \begin{aligned}I_{P,z} &= I_{C,z} + m {r_{CP}}^2 \\&= \frac{1}{12} m \ell^2 + m \left(\frac{\ell}{2}\right)^2 \\&= \frac{1}{3} m \ell^2.\end{aligned}\ $$

The moment of inertia $ I_{P,x} $ is still zero, because $ \vec{r}_{CP} $ is parallel to $ x $.

Solid cylinder or disk: moments of inertia #rem-ek

$$ \begin{aligned}I_{C,x}&=I_{C,y}=\frac{1}{12}m(3r^2+\ell^2)\\I_{C,z}&=\frac{1}{2}mr^2\end{aligned} $$

The solid cylinder expressions are simply the cylindrical thick shell formulas #rem-ey with the inner radius set to $ r_1 = 0 $ and the outer radius $ r_2 = r $ .

Hollow cylinder or hoop: moments of inertia #rem-eh

$$ \begin{aligned}I_{C,x}&=I_{C,y}=\frac{1}{12}m(6r^2+\ell^2)\\I_{C,z}&=mr^2\end{aligned} $$

The hollow cylinder expressions can be found from cylindrical thick shell formulas #rem-ey by taking the same value for both inner and outer radii, so that $ r_1 = r_2 = r $ .

Solid ball: moments of inertia #rem-eb

$$ \begin{aligned}I_C&=\frac{2}{5}mr^2\end{aligned} $$

All axes through $ C $ have the same moment of inertia.

The solid ball moment of inertia can be directly obtained from the spherical thick shell expression #rem-es with inner radius $ r_1 = 0 $ and outer radius $ r_2 = r $ .

Hollow sphere: moments of inertia #rem-ew

$$ \begin{aligned}I_C&=\frac{2}{3}mr^2\end{aligned} $$

All axes through $ C $ have the same moment of inertia.

A hollow sphere moment of inertia is the same as that for the spherical thick shell #rem-es with inner radius and outer radius both set to $ r_1 = r_2 = r $. Some care is needed here, however, as a simple substitution into the spherical thick shell expression would give the undefined value $ 0 / 0 $ .

Instead we need to set $ r_2 = r $ and then to take the limit as $ r_1 \to r $ using l'Hôpital's rule:

$$ \begin{aligned}I_C &= \lim_{r_1 \to r} \frac{2}{5} m\left(\frac{r^5 - {r_1}^5}{r^3 - {r_1}^3}\right) \\&= \lim_{r_1 \to r} \frac{2}{5} m\left(\frac{\frac{d}{d r_1}\left(r^5 - {r_1}^5\right)}{\frac{d}{d r_1}\left(r^3 - {r_1}^3\right)}\right) \\&= \lim_{r_1 \to r} \frac{2}{5} m\left(\frac{5 {r_1}^4}{3 {r_1}^2}\right) \\&= \lim_{r_1 \to r} \frac{2}{3} m {r_1}^2 \\&= \frac{2}{3} m r^2.\end{aligned}\ $$

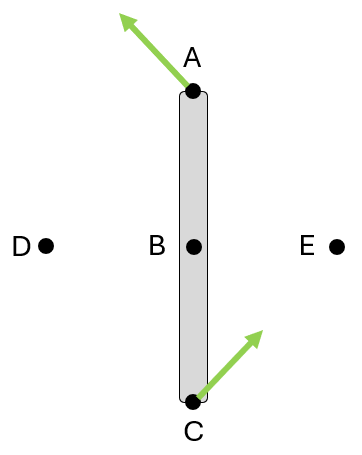
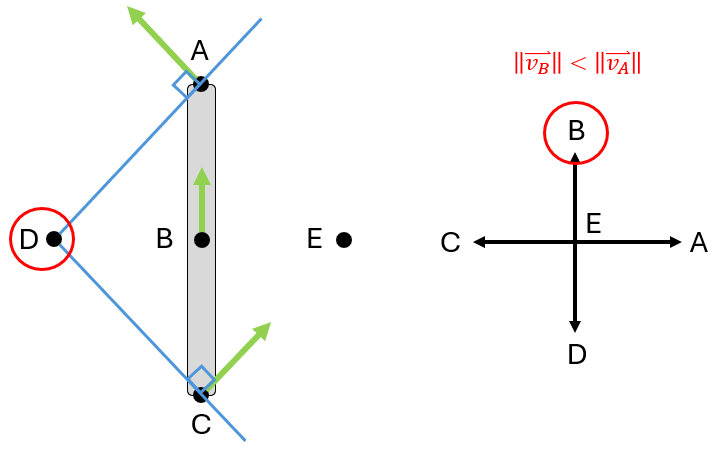
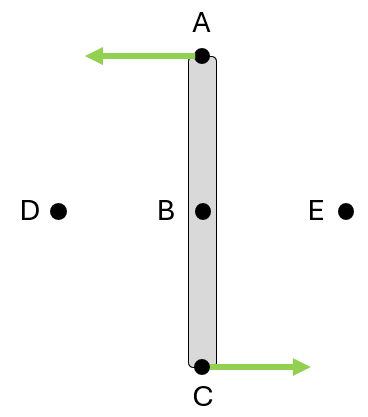
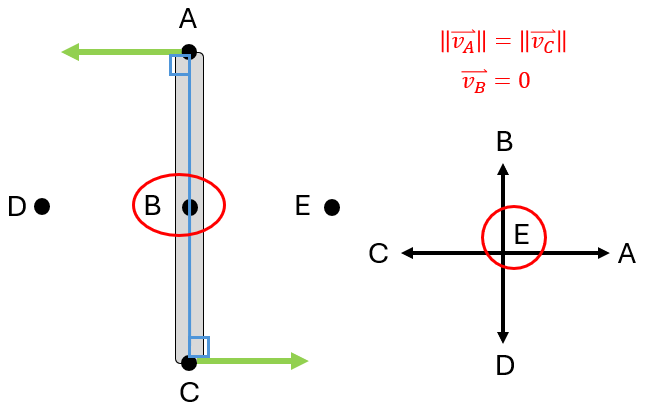
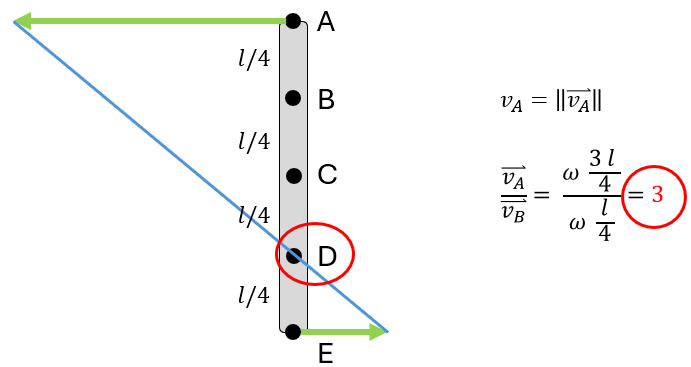
Instantaneous center (M)

For a rigid body moving in 2D (rotating and possibly translating)
Instantaneous center “M” is the point on or off the rigid body that has zero velocity at that instant (i.e. no translation at this point)
Point that the body rotates about (at that instant in time)

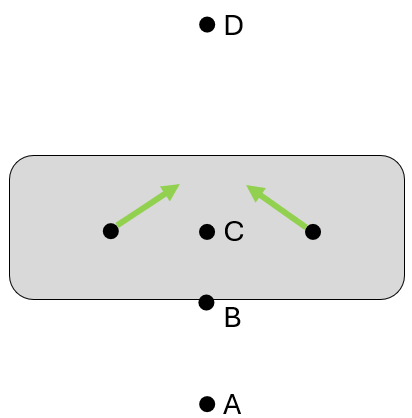
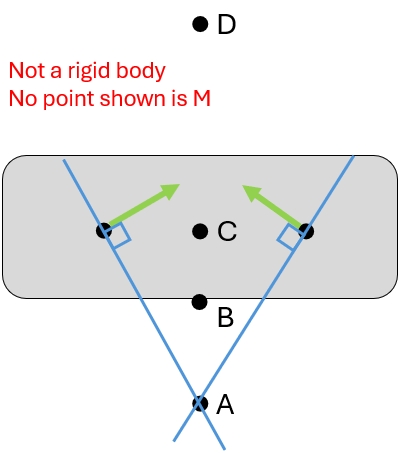
Graphical rules for finding M

(Assuming that figure is drawn to scale, including velocity vectors)

Draw lines perpendicular to velocities

If the lines intersect at a single point, that point is M
If the lines are colinear:
- Draw 2 lines that connect the tips of velocity vectors
- If the lines intersect at a single point, that point is M

Example Problem: Equal velocity magnitudes in different directions. #rbk-rbe

Find the instantaneous center (M) and the direction of $ \vec{v}_B $ of the beam.

Example Problem: Equal velocity magnitudes in opposite parallel directions. #rbk-rbp

Find the instantaneous center (M) and the direction of $ \vec{v}_B $ of the beam.

Example Problem: Different velocity magnitudes in opposite parallel directions. #rbk-rbc

Find the instantaneous center (M) and the direction of $ v_A / v_B $ of the beam.

Example Problem: Equal velocity magnitudes in the body. #rbk-rbm

Find the instantaneous center (M).

Example Problem: Equal velocity magnitudes in same paralled direction. #rbk-rbn

Find the instantaneous center (M).

The body is not rotating

Warning: Pay attention to: #icm-wa

Consistent direction of rotation.
Consistent speeds $ v = \omega \, r $.
Body may not be rotating (pure translation).

Applications

Accelerating and braking

2D rigid body model

Consider a car sitting stationary on the ground, as shown below. We will take the entire car plus wheels to be a single rigid body. Clearly this is inaccurate (the wheels can't turn), but it is still useful.

We start with the car stationary, sitting on the road. Gravity acts downward through the center of mass, while there are upwards reaction forces on the wheels and corresponding equal and opposite forces downwards on the ground. Because the car is not accelerating, the total forces on the car are in balance, as we can see on the .

When the driver , this results in the car pushing back on the road, giving a net forward force on the driving wheels (the back wheels for our car), and the car accelerates up to cruising speed. Here we are including air resistance but neglecting rolling resistance, and while cruising at constant speed the driving force exactly balances the drag force from air resistance. When the driver , the car pushes on the road to slow down, giving backward forces on both wheels and causing the car to decelerate to a stop.

Repeat the / cycle a few times while showing the . Observe the horizontal and vertical forces of the road on the car wheels. Also view the forces both in and as total force vectors.

The vertical forces of the road on the car always need to balance the gravitational force, but we can see that the distribution between front and rear wheels changes as the car accelerates and decelerates. This is because the horizontal driving and braking forces are below the center of mass and produce a moment. The vehicle is not rotating, so this moment must be counteracted by the ground forces. The force directions mean that the rear wheels take more weight during acceleration, while the front wheels take more weight during braking.

Traction, acceleration, and braking

The maximum force with which the car can push against the road is limited by the friction coefficient of the tire multiplied by the normal force. This applies both during acceleration and braking.

To accelerate as hard as possible, we should thus use a rear-wheel drive layout. If we accelerate too hard, however, then the back wheels will slip and experience wheelspin, because the dynamic coefficient of friction is lower than the static coefficient. While high-performance applications generally want to maintain traction in all cases, the impressive effects of traction loss are sometimes deliberately produced. Spinning the rear wheels in a burnout produces smoke as the tires vaporize due to the heat from friction. Drag racers perform a burnout at the start of a race to clean the tires and heat them to an optimal temperature. To easily produce a burnout a line lock can be installed to enable the brakes to be applied only to the front wheels (although this is often illegal on street cars). Alternatively, a burnout can be performed by disengaging the clutch, running the engine at a high revs, and then rapidly engaging the clutch. The high angular momentum of the engine then provides a rotational impulse to the rear wheels, causing them to lose traction.

Even if traction is maintained during acceleration, a second problem that may occur is that the torque from the rear wheels can be enough to lift the front wheels off the ground, so that the vehicle performs a wheelie. This occurs very easily for motorbikes and BMX bicycles, due to a high center of mass to wheelbase ratio, but can also occur for cars with poor geometry and sufficient power.

The problems of wheel slip and wheel lift-off occur in reverse while braking. Any car with well-maintained brakes has sufficient braking power to cause the wheels to lock, even in dry conditions with good traction. For this reason many cars now include anti-lock braking systems (ABS), which detect wheel locking and rapidly pulse the brake force to prevent locking. Even better than this are electronic brakeforce distribution (EBD) systems, which apply the maximal brake force to each wheel while maintaining traction and control, better than any unassisted human driver could achieve. Due to the weight transfer to the front wheels during braking, the front brakes generally apply much greater force and thus wear out sooner than the rear brakes.

Did you know?

Using ABS to mean Anti-lock Brake System is an example of a backronym. This is where the name ABS came first, and then Anti-lock Brake System was made up later to fit the letters as an ackronym. In fact ABS comes from the German phrase Antiblockiersystem (literally: Anti Locking System).

Traction, acceleration, and braking

To understand how forces and moments act on the wheels, we need to separate out the single rigid-body model into multiple rigid bodies. The simplest version of this has one rigid body for the body, and four rigid bodies for the wheels. We will assume that the two front wheels always act as a pair (same forces, same motion), and similarly for the two back wheels.

Again we start with the car stationary, and on the we see the balance of vertical forces. Remember that the force shown on each wheel is really doubled, as there are two front and two rear wheels.

If we now , then we see a clockwise moment applied to the rear (driving) wheels. This causes the wheel to rotate, but friction forces means that it must roll without slipping, so there must be a forward contact force causing it to accelerate forwards. Counteracting this is a backwards reaction force from the car on the wheel. On the car we see that there are equal and opposite forces and moments at the axles. Just as in the single rigid body case, we have a net horizontal force causing forward acceleration, and moment balance means that the weight of the car is transferred primarily to the rear wheels.

applies backwards moments to both wheels, causing them to slow down. To maintain non-slip, there is a backwards force from the ground at the point of contact. Because the wheel is slowing down, the car pushes forward on the axle. The ground/axle forces are trying to rotate the wheel forward, which must be counteracted by the braking moment. The braking moment is thus counteracting both the rotational inertia of the wheel, as well as the force couple from the ground/axle forces. Of these, the force couple is much larger (stopping a wheel without the car attached would be comparatively easy for the brakes). During braking we see again the weight being transferred to the front wheels.

More complex models

While we can learn a lot about car performance from the simple rigid body and multi-body models, there is a great deal of physics neglected by these models, which can be important for engineering design.

Both the car and the tires are deformable bodies. The deformation of the tire is responsible for the contact patch which generates the friction forces that allow a car to accelerate and brake. The physics of the frictional contact between the tire and ground can be very complex, as can the geometry of the tire. Modern tires have complex tread patterns with grooves and lugs that are designed to channel away water and snow, maintaining traction even in challenging conditions.

As well as being individually deformable, the wheels are are not rigidly connected to the car body as above, but they are actually connected by a suspension system, consisting of linkages, springs, and shock absorbers. These enable both a comfortable ride and safe handling of the vehicle.

The simple models above included a simple model of air resistance, but they neglected rolling resistance. This is the force primarily produced by the tire being compressed and re-expanded at the contact with the ground as it rolls, producing a backward force on the wheel. Using steel wheels on steel can result in trains having up to ten times lower coefficients of rolling resistance than car tires, which is one reason for the efficiency of rail transport.

Did you know?

There is evidence that the wrinkling of fingers in water may serve the same purpose as tread patters on tires, improving traction in wet conditions by forming channels to carry away water. This hypothesis is supported by the fact that finger wrinkling relies on an active nervous system response, meaning that the fingers of corpses cannot wrinkle (but what about zombies' fingers?).

Brake system design

The above model shows equal brake force applied on the front and rear wheels. This both inefficient and dangerous, as the rear wheels will lock while the front wheels are still turning. See #avs for steering and sliding. We want to apply more force on the front brakes, so that we can deliver the most total force while still having no sliding. This can be achieved by electronic brakeforce distribution (EBD) systems, however traditional systems are also possible.

The basic outline of a brake system is that the brake pedal pushes on a master cylinder, which compresses hydraulic brake fluid in the brake lines. This then pushes on slave cylinders in each wheel, which push the brake pads onto the brake rotors (for disc brakes; drum brakes are somewhat different). The combination of slave cylinders and brake pads and their housing is called a brake caliper.

To apply more force to the front brakes, one simple system used in practice is to have the front-wheel slave cylinders have a larger diameter than those on the rear wheels. Because the pressure in the brake lines is the same everywhere, the force exerted by the pistons is proportional to their cross-sectional area, resulting in more force with the larger-diameter front-wheel cylinders.

Modern cars use more advanced systems. The master cylinder typically contains two pistons in a parallel arrangement, so that it can apply pressure to the front or rear brake lines even if the other brake line develops a leak. A metering valve applies pressure to the rear brakes before the front, improving vehicle steering stability and allowing mixed drum/disc systems to be used. A pressure differential valve detects brake hydraulic leaks by sensing different front/rear line pressures. A proportioning valve assists with applying a different pressure distribution to the rear brakes.

Car model

This is a 1965 Ford Mustang Fastback. The mass of the car body is 1100 kg and each of the wheels has mass 20 kg, giving a total mass of 1180 kg. We assume that the wheels are uniform cylinders. The dimensions of the car are shown below.

$$ \begin{aligned} h_1 &= {0.31\rm\ m} & \ell_1 &= {0.98\rm\ m} \\ h_2 &= {0.29\rm\ m} & \ell_2 &= {1.41\rm\ m} \\ h_3 &= {0.79\rm\ m} & \ell_3 &= {1.41\rm\ m} \\ & & \ell_4 &= {0.80\rm\ m} \end{aligned} $$

The force of air resistance was computed above using the quadratic drag equation which is a good approximation for medium- to high-velocity motion in air:

$ F_{\rm D} = \frac{1}{2} \rho v^2 C_{\rm D} A $

Here $ F_{\rm D} $ is the drag force, $ \rho = 1.23\rm\ kg/m^3 $ is the air density, $v$ is the velocity, $ C_{\ D} $ is the drag coefficient (taken to be 0.3 for the Mustang), and $A$ is the reference area (approximately the cross-sectional area, taken to be $2.2\rm\ m^2$ for the Mustang).

Banked turns

2D Rigid body model

We now use a single rigid body model for the bus and we will do everything in 2D. Below we see a front-on diagram of the bus, with the inside of the track to the left. If we turn on the , then we see that the weight of the bus is supported by two forces, one on each wheel. If we increase $\theta$ then the weight is supported more by the down-slope wheel, and we also see sideways friction forces appear to stop the bus from sliding. If the slope becomes too steep, then the normal force on the up-slope wheel reverses direction, indicating that it is holding the wheel down onto the road. Physically this cannot happen, so at this point the bus would tip over. We needed this rigid-body model to understand this tipping behavior, as we couldn't model this with the point mass model. Depending on the value of the friction coefficient, the bus may either slide or roll first as $\theta$ increases.

Road bank angle: $\theta = $ 45$^\circ$

Bus speed: $v = $ 30 $\rm m/s$

If we now set the bank angle $\theta$ back to zero, we can start to increase the speed $v$. Now we see that the wheel on the inside of the track takes less of the weight, and the friction forces now stop the bus from sliding outwards on the track. If the bus goes too fast then it will roll outwards on the track (assuming the friction coefficient is high enough that it didn't slide first).

Having considered both a banked road with stationary bus, and a moving bus on a horizontal road, we can now combine them to see the advantage of having a banked road when the bus is cornering. Choose a bus velocity, and then change the bank angle $\theta$, so that the friction force is reduced (helping to avoid sliding) and the normal forces on the wheels are more evenly balanced (helping to avoid rolling). For any given speed, we can choose a bank angle so that there is simultaneously no sideways friction force and also exactly balanced normal forces. This is the safest bank angle for this speed.

Design of roads, tracks, and rail

A straight road generally has the center somewhat higher than the edges to allow water to run off. This is called cross slope or camber. When it is desired to have a banked turn, then the outer edge of the road is raised to produce superelevation, with the outer edge rising above both the center and the inner edge. The bank angle is chosen based on the radius of curvature of the turn and the expected speed of cars going around the turn, while still allowing for the fact that cars might be moving slowly or even stopped. The angle should thus not be chosen to eliminate all friction forces when cars are traveling at maximum speed, as this would be dangerous if traffic had to stop on the road.

Velodromes are arenas with tracks designed for high-speed bicycle races, as shown below, with speeds up to 85 km/h. The bank angle on velodrome tracks is chosen to minimize sideways forces on the bicycles when they are traveling at near maximum speeds, so the angle chosen depends on the radius of curvature of the track corners. For example, the Blaine velodrome track pictured below is 250 m long and has a 43° bank angle on the corners and 15° banking on the straightaways.

Bicycle riders on a banked turn at the Blaine velodrome, part of the National Sports Center in Blaine, Minnesota. Image source: flikr user flyinfoto (CC BY 2.0) (full-sized image).

High-speed trains such as the French TGV operate at speeds of over 300 km/h and have run at up to 575 km/h. To accommodate cornering at such speeds, track bends are constructed with a large radius of curvature (at least 7 km for new tracks) and a bank angle of up to about 7° (180 mm maximum superelevation with Standard gauge of 1435 mm). For railways, banking the track is know as cant.

An alternative approach for cornering with trains is to leave the track relatively flat and to tilt the train as it travels around a corner. This allows high-speed trains to operate on regular tracks, while maintaining safety and comfort for the passengers. For example, the Queensland Rail Tilt Train operates at 180 km/h by tilting at up to 5° around corners. As we see from our rigid body analysis above, tilting the train will help with avoiding tipping over at high speeds, but will not help with reducing horizontal friction forces. Even with a tilting train, entering a curve at too high a speed will lead to disastrous results.

Did you know?

The Blaine velodrome in Minnesota was designed by the famous Schuermann velodrome architects and built from the extremely durable African Afzelia hardwood. Velodrome races are always counter-clockwise and use special bikes with fixed chains (no freewheeling, no gears) and no brakes. The corners are scarily steep:

Image credit: Tom McGoldrick (full sized image).

Did you know?

High-speed trains such as the French TGV and German ICE require many sophisticated engineering techniques to enable travel at extreme speed. Very smooth rails are needed, so the track is formed by welding the segments together into one precisely-aligned continuous steel line. The steel rails conduct heat too well for conventional welding, so thermite welding is used to join the track segments.

At high speeds the train drivers are unable to see railway signals on the side of the track. Electronic signaling systems are used to communicate to the drivers, either through the tracks for the TGV or via additional cables for the ICE.

Friction-based brakes produce too much heat, as they would need to absorb the kinetic energy of several hundred tonnes of train moving at over 300 km/h. Instead, dynamic breaking is used, in which the electric motors powering the trains are run in reverse as generators and the energy is shed as heat in resistor arrays. At extremely high speeds, the wheels themselves cannot provide sufficient traction to enable braking, so technologies like magnetic induction brakes are being developed, which directly push against the rails without involving the wheels at all.

Bus model

The bus model used above is a Setra S 411 HD coach. The mass of the vehicle is 12.6 t and the dimensions are shown below.

$$ \begin{aligned} h_1 &= {0.31\rm\ m} & \ell_1 &= {0.98\rm\ m} \\ h_2 &= {0.29\rm\ m} & \ell_2 &= {1.41\rm\ m} \\ h_3 &= {0.79\rm\ m} & \ell_3 &= {1.41\rm\ m} \\ & & \ell_4 &= {0.80\rm\ m} \end{aligned} $$