Cartesian coordinates
Cartesian coordinates (also known as rectangular coordinates) are the regular \(x,y\) or \(x,y,z\) coordinates in 2D and 3D, with perpendicular straight-line axes.
| coordinate | name | range | definition |
|---|---|---|---|
| \(x\) | horizontal | \(-\infty \lt x \lt \infty\) | horizontal distance from the \(y\)-axis |
| \(y\) | vertical | \(-\infty \lt y \lt \infty\) | vertical distance from the \(x\)-axis |
In 3D the \(x\),\(y\),\(z\) axes are oriented in right-handed order, so that fingers curling from \(x\) to \(y\) means the thumb points in the \(z\) direction.
Cartesian coordinate system, showing the origin \(O\) and three positions with their coordinates.
Notation note
When writing coordinates we can either list the coordinate values explicitly, like \(x = 2\), \(y = 1\), or we can just write the numbers in an ordered list, like \( (2, 1) \).
Writing them as a list assumes that we know which coordinate system we are using, and which order the coordinates are in. We will typically write the coordinate values explicitly to avoid confusion. This also applies to vector components.
Vector bases
To describe vectors mathematically, we write them as a combination of basis vectors. An orthonormal basis is a set of two (in 2D) or three (in 3D) basis vectors which are orthogonal (have 90° angles between them) and normal (have length equal to one). We will not be using non-orthogonal or non-normal bases.
Any other vector can be written as a linear combination of the basis vectors:
The numbers \(a_1, a_2, a_3\) are called the components of \( \vec{a} \) in the \( \,\hat{\imath}, \hat{\jmath}, \hat{k} \) basis. If we are in 2D then we will only have two components for a vector.
Writing a vector as the sum of scaled basis vectors. The scale factors are the components of the vector. Here \( \vec{a} = 3\hat\imath + 2\hat\jmath \), so the components of \( \vec{a} \) are \(a_1 = 3\) and \(a_2 = 2\).
We draw the symbol \(\odot\) (arrow tip) to indicate a vector coming out of the page, and \(\otimes\) (arrow fletching) to indicate an arrow going into the page.
Two standard arrangements of the basis vectors when working in 2D. Either \(\hat\jmath\) is the vertical and \( \hat{k} \) is out of the page, or \( \hat{k} \) is the vertical and \(\hat\jmath\) is into the page. In both cases \(\hat\imath\) is horizontal.
Notation note
Just as for position coordinates, we can write the vector components \(3\hat\imath + 2\hat\jmath\) as the ordered list \((3, 2)\) if we know which basis we are using. Because we often will be using several bases simultaneously, we will generally write the components explicitly in the \(3\hat\imath + 2\hat\jmath\) form.
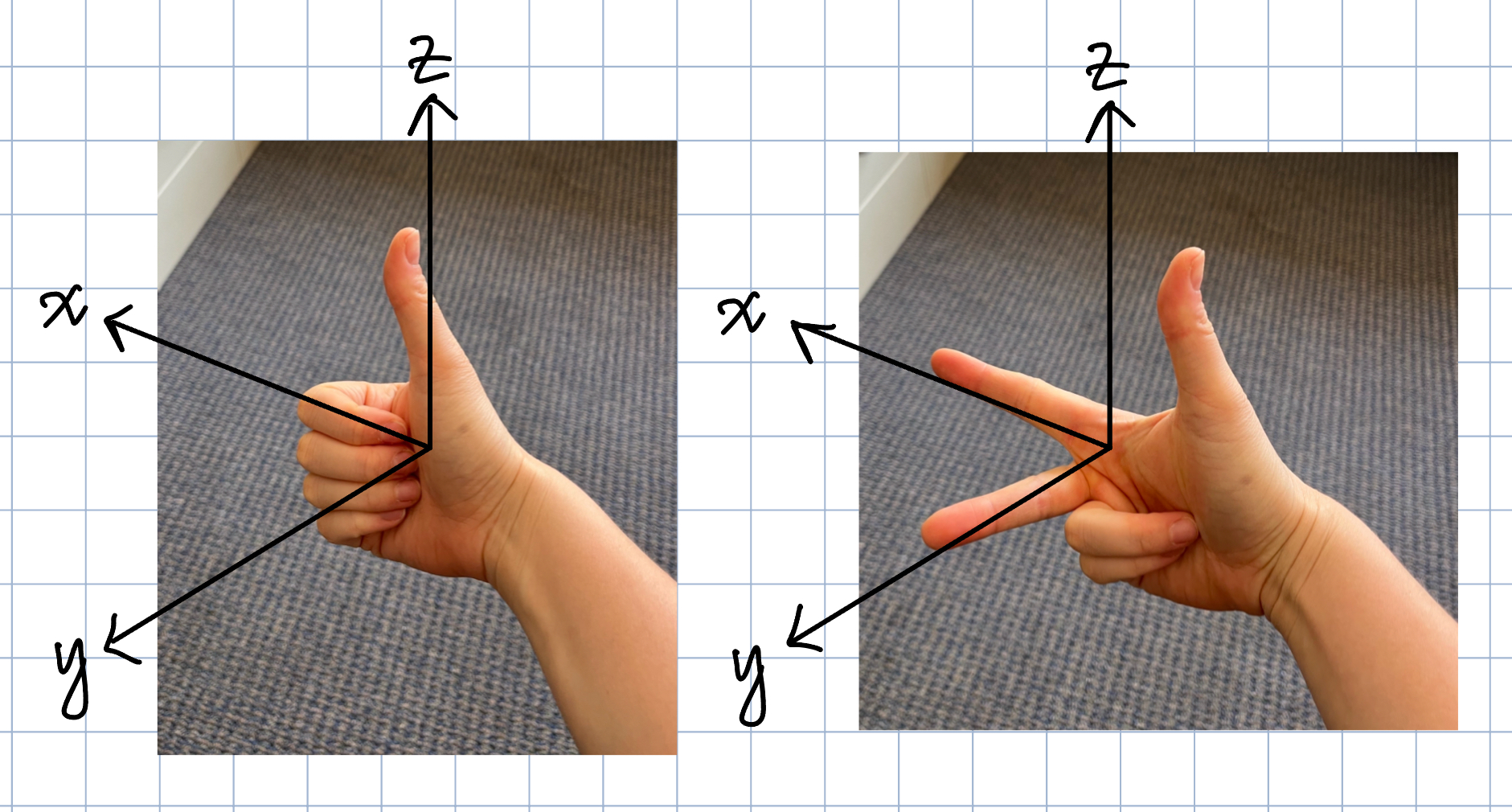
Right hand rule
The Cartesian system is a "right-handed" coordinate system, which means that we can use the right-hand rule to determine the direction of the \( x, y \) and \( z \) axes. In 3D the \( x, y, z \) axes are oriented in right-handed order, so that fingers curling from \( x \) to \( y \) means the thumb points in the \( z \) direction. We can also use the individual fingers on our right hand, where our pointer finger points in the x-direction, our middle finger points in the y-direction, and our thumb points in the z-direction.