Introduction to Stress Concentrations

In mechanical engineering, "stress concentration" refers to the increase in stress around small features like holes, notches, or sharp corners in a material.

Imagine you're trying to tear a piece of paper. If you pull it from both ends, it's tough to rip. But if you make a small cut (a notch) first, the tear spreads easily from there. This happens because stress (force per unit area) gets concentrated around sharp edges or holes.

Actual Stress Distribution vs Nominal Stress

Imagine a metal plate like the one shown in Figure 1, with a hole in the middle, being pulled from both ends. The stress (force per area) is not evenly spread across the plate. Instead, it is concentrated near the edges of the hole. This introduces a relationship between the Nominal Stress and Maximum Stress (\( \sigma_{nom} \) and \( \sigma_{max} \) respectively) related by the Stress Concentration Factor (\( K_t \)).

Their relationship can be defined as follows:

Nominal Stress: The average stress.
Maximum Stress: The highest stress, which occurs at the edge of the stress concentration.
Concentration Factor: A number that tells us how much the stress is increased due to the stress concentration.

For example, if \( K_t=3 \) , then the highest stress (Located at the edge of the hole, crack, or notch) is three times the applied stress.

Example Problem

Consider the steel plate below, with a width of \( 100 \; mm \) and a thickness of \( 10 \; mm \) is subjected to a tensile force of \( 20 \; Kn \). The plate has a circular hole with a diameter of \( 20 \; mm \) at its center. The stress concentration factor for this geometry is given as \( K_t = 3 \).

What is the Nominal stress \( \sigma_{nom} \)?
What is the Maximum Stress \( \sigma_{max} \)?

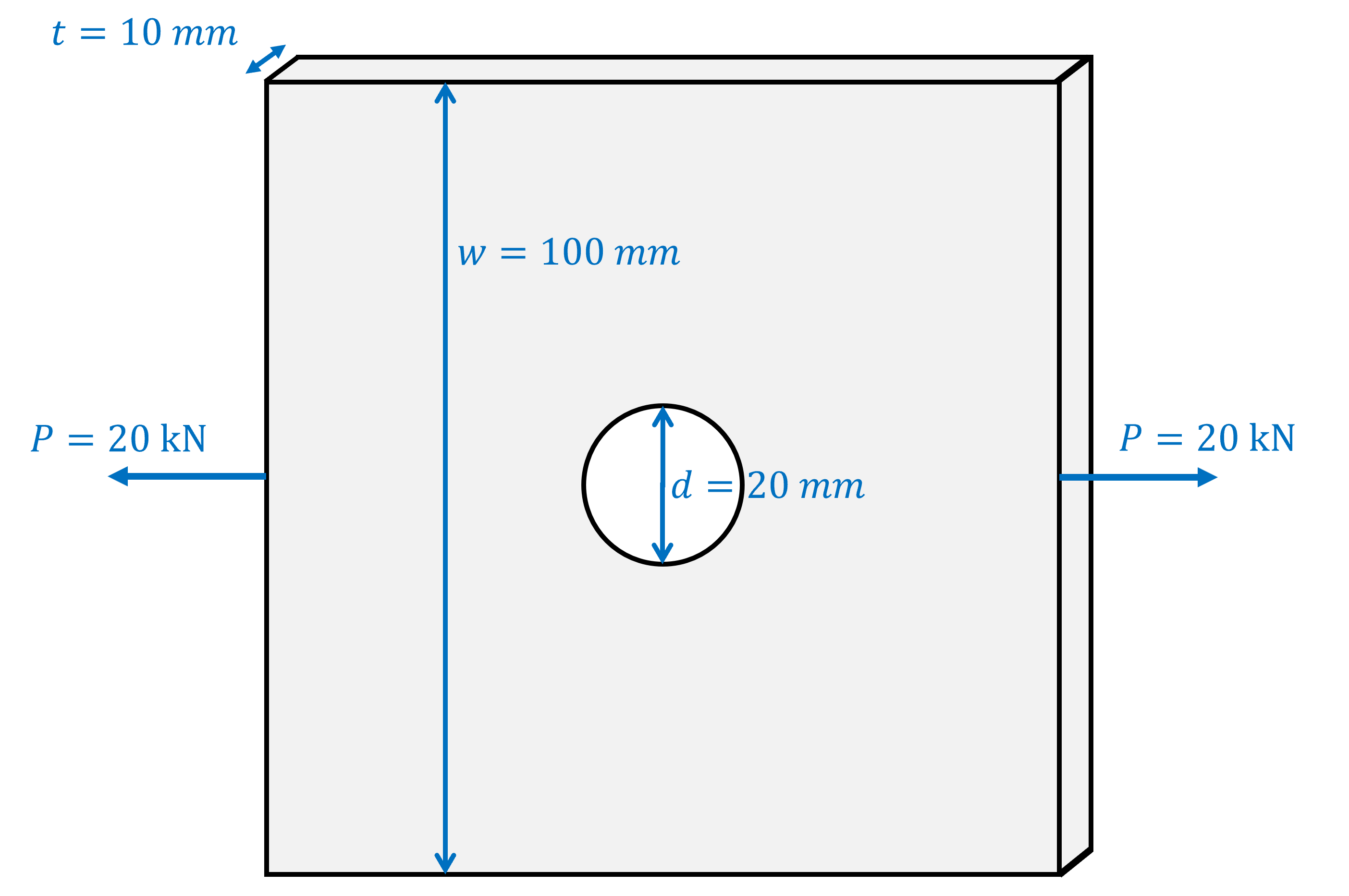
Figure 1: Sample stress concentration problem

Step 1: Compute the Nominal Stress

\( A= (W-d) \times t= (100 - 20) \times 10 = 800 \text{ mm}^2 \)

Thus, the nominal stress is:

\( \sigma_{\text{nom}} = \frac{20,000 \text{ N}}{800 \text{ mm}^2} = 25 \text{ MPa} \)

Warning: Computing Cross Sectional Area #stress_concentration_warning

The diameter of the hole must be subtracted from the height of the plate to calculate the correct cross sectional area.

Step 2: Compute the Maximum Stress

The maximum stress \( \sigma_{\text{max}} \)

\( \sigma_{\text{max}} = K_t \times \sigma_{\text{nom}} \)

\( \sigma_{\text{max}} = 3 \times 25 \text{ MPa} = 75 \text{ MPa} \)

Application of Stress Concentrations

What happens if the stress exceeds the yield strength of the material? Plastic Deformation

As we increase the stress on an object, we know that the the stress can’t keep increasing past a certain limit, called the yield strength \( S_y \) of the material.

If stress exceeds the yield strength of the material, plastic deformation will occur. If the stress is evenly distributed across the entire object, this plastic deformation will often cause the object to fail.

However, if a stress concentration is present, it is possible for the maximum stress to exceed the yield strength of the material, while the nominal stress remains below the material's yield strength.

Once yeilding occurs:

Some areas reach their maximum stress limit and start deforming permanently. This means that these areas cannot bear any additional stress.
As a result, the stress that was supposed to be born by these area is instead redistributed to other areas in a process called load redistribution.
This makes the stress spread out.

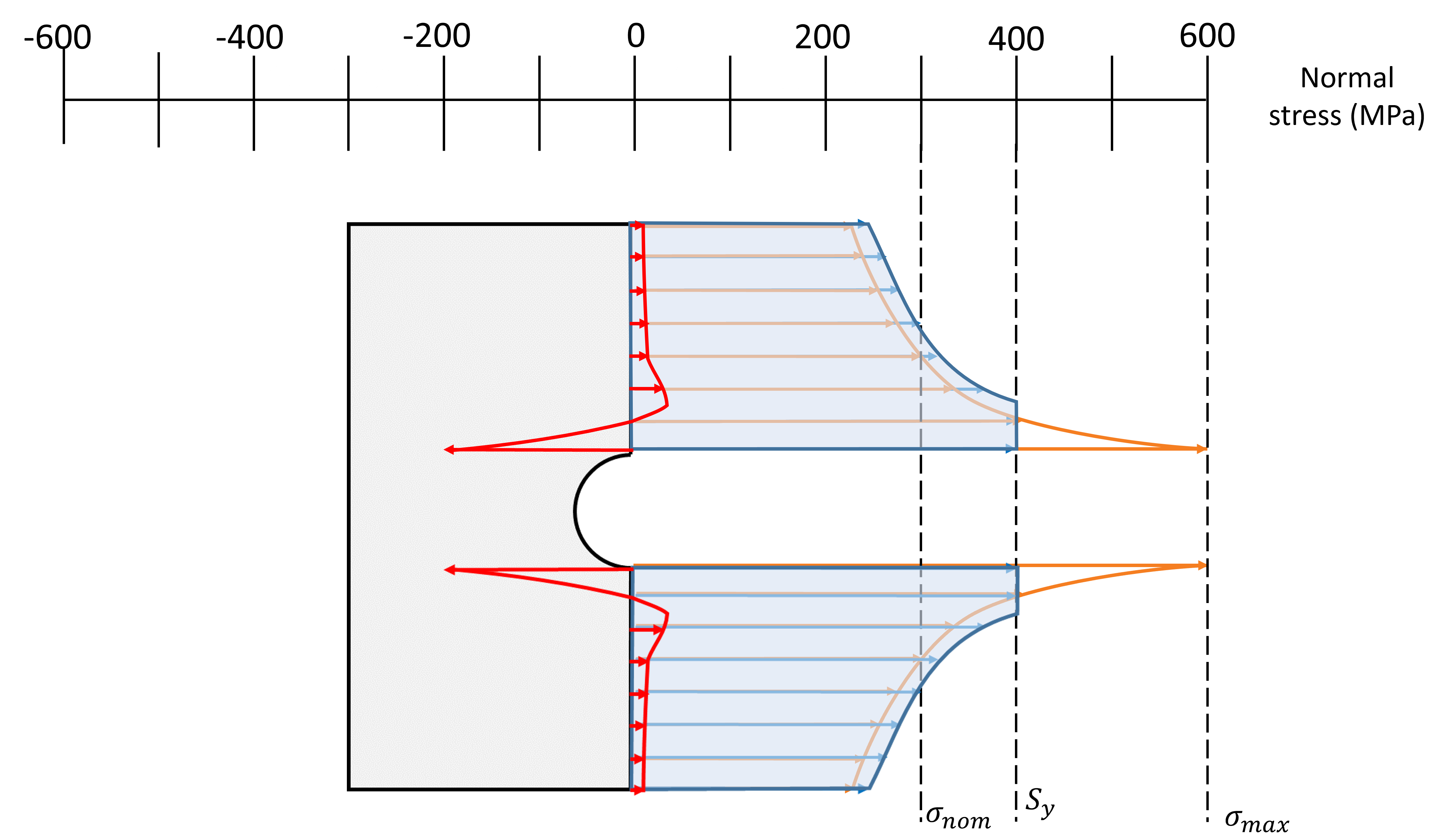
Figure 2: Diagram of Stress Redistribution

In figure 2 we can see this process in a little more detail:

The orange curve shows the stress that is applied to the object assuming the material stays elastic (no permanent deformation).
The vertical dashed lines, \( \sigma_{nom} \),\( S_y \),and \( \sigma_{max} \) represent the nominal stress, the yield strength and the maximum stress respectively
he blue curve shows the redistributed stress that the material experiences after plastically deforming and redistributing the stress. Note that the nominal stress is the same, as the decrease in stress near the stress concentration is offset by an increase in the stress further away from the stress concentration.

Residual Stresses After Unloading

After the external force is removed, the object will try to return to its original shape. Elastic deformation will be recovered but the plastically deformed regions cannot return to their original form. Due to this, some stresses remain inside the material. These are called residual stresses, and it can be calculated by subtracting the elastic stress (shown in orange) from the actual stress (shown in blue).

Design Considerations

As an engineer, it is important to know when we should consider the effects of stress concentrations, as well as times that the effects of stress concentrations can be safely ignored.

In general, stress concentrations can be safely ignored when the material in question is ductile. This is because the material can yield locally, and redistribute stresses. Even if local plastic deformation does occur, it is unlikely to cause the object as a whole to fail.

However, there are several situations were it is imperative to consider the impact of stress concentrations.

Brittle materials may fracture rather than yield locally, so a stress concentration can cause catastrophic failure.
Impact or dynamic loading may cause stresses to be applied so quickly that they cannot be adequately redistributed, causing failure.
Repeated loading can cause fatigue failure due to cyclic loading. In these scenarios the presence of stress concentrations can accelerate the process of fatigue failure and should be considered.