Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Moment of Inertia

    Note: in statics we are using the second moment of area as our moment of inertia. In dynamics, a different moment of inertia is used (the mass moment of inertia). The differences between these two quantities are summarized in the following table.
    Mass moment of inertiaArea moment of inertia (used in Statics!)
    Other names Second moment of area
    Description Determines the torque needed to produce a desired angular rotation about an axis of rotation (resistance to rotation) Determines the moment needed to produce a desired curvature about an axis(resistance to bending)
    Equations
    $$ I_{P,\hat{a}} = \iiint_\mathcal{B} \rho r^2 \,dV\ $$
    $$ I_x = \int_{A}^{} y^2 \,dA \ $$
    $$ I_y = \int_{A}^{} x^2 \,dA \ $$
    $$ \begin{aligned} J_O &= \int_{A}^{} r^2 \,dA \\ &= \int_{A}^{} (x^2+y^2) \,dA\ \end{aligned} $$
    Units\( length*mass^2 \)\( length^4 \)
    Typical Equations
    $$ \tau = I\alpha $$
    $$ \sigma = (My)/I \ $$
    Courses TAM 212 TAM 210, TAM 251

    Moment of Inertia (Second Moment of Area)

    The moment of inertia used in statics is the "second moment of area". This is a mass property that determines the amount of torque that is needed to create an angular acceleration about a specific axis of rotation. The dimension of the area moment of inertia is \( length^4 \).
    Moment of inertia about the x-axis
    $$ I_x = \int_{A}^{} y^2 \,dA \ $$
    Moment of inertia about the y-axis
    $$ I_y = \int_{A}^{} x^2 \,dA \ $$
    Polar moment of inertia.
    $$ J_O = \int_{A}^{} r^2 \,dA = \int_{A}^{} (x^2+y^2) \,dA\ $$
    Note: the polar moment of inertia depicts the measure of the distribution of area about a point (usually the origin), rather than about an axis.

    Parallel axis theorem

    The parallel axis theorem is used to calculate the moment of inertia for an object around axes other than through the centroid.

    Parallel axis theorem.
    $$ \begin{align} I_{x} = I_{x'} + A(d_y)^2 \\ I_{y} = I_{y'} + A(d_x)^2 \end{align} $$

    where \( I_{x'} \) and \( I_{y'} \) are the moments of inertia about the centroid, \( A \) is the total area of the shape, and \( d \) is the perpendicular distance from the centroid to the axes of interest in either the x or y directions.

    Combining moments of inertia

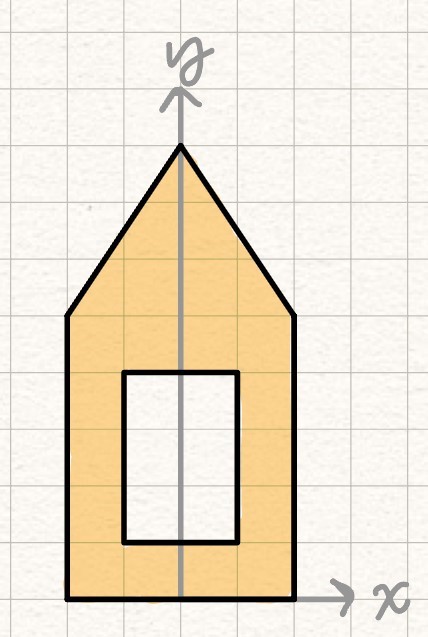
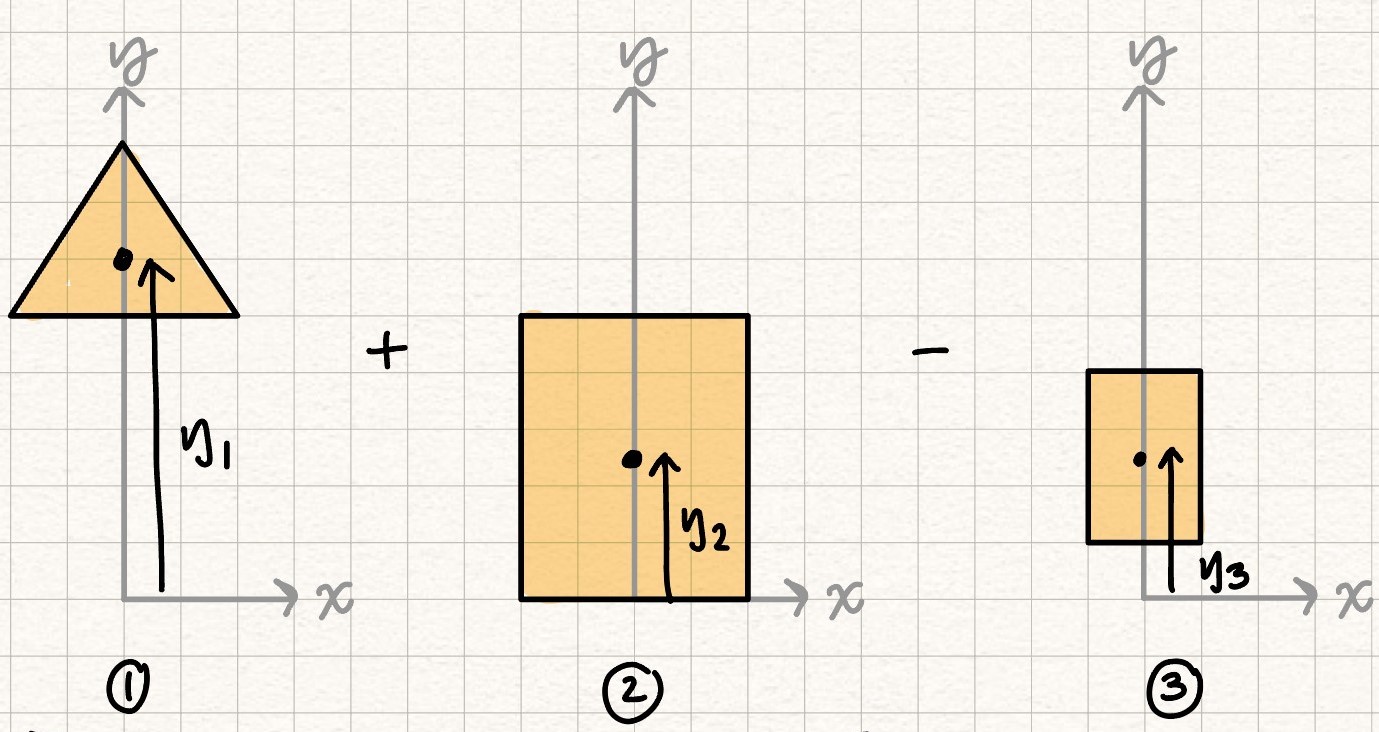
    Moments of inertia of simple shapes can be combined to calculate the moments of inertia of more complex shapes using the parallel axis theorum.

    Example Problem: Find the moment of inertia of a composite shape. #blt-fst

    What is the \( I_x \) of the composite shape?

    $$ I = I_1 + I_2 - I_3 $$
    $$ I_1 = I_{x_1'}+A_1y_1^2 $$
    $$ I_2 = I_{x_2'}+A_2y_2^2 $$
    $$ I_3 = I_{x_3'}+A_3y_3^2 $$

    Moment of inertia for typical shapes

    Common shapes about the origin: \( I \) and \( J_O \)
    Common shapes about the centroid: \( \bar{I} \) and \( J_c \)
    ShapeDiagramMoI about the centroid (centroidal axis)MoI about the origin
    Rectangle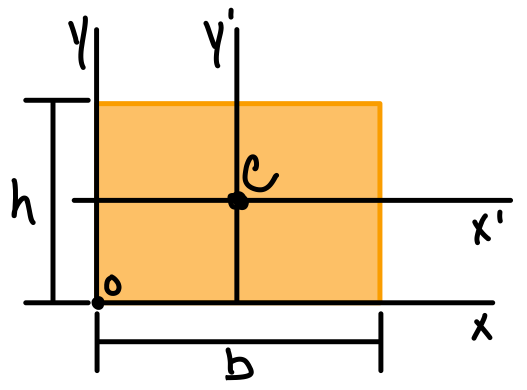
    		\( \bar{I_{x'}} = \frac{1}{12}b h^3 \)

    \( \bar{I_{y'}} = \frac{1}{12}b^3 h \)

    \( J_c = \frac{1}{12}bh(b^2+h^2) \)    		\( I_x = \frac{1}{3}b h^3 \)

    \( I_y = \frac{1}{3}b^3 h \)

    Triangle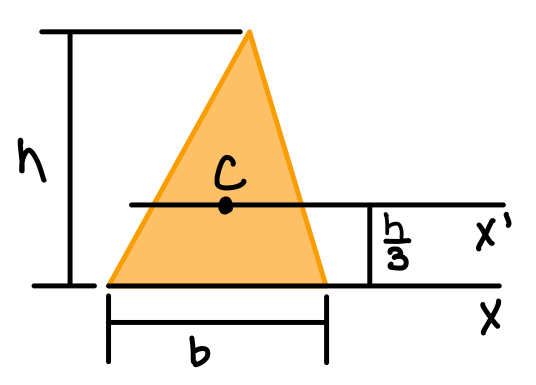
    		\( \bar{I_{x'}} = \frac{1}{36}bh^3 \)

    		\( I_x = \frac{1}{12}bh^3 \)
    Circle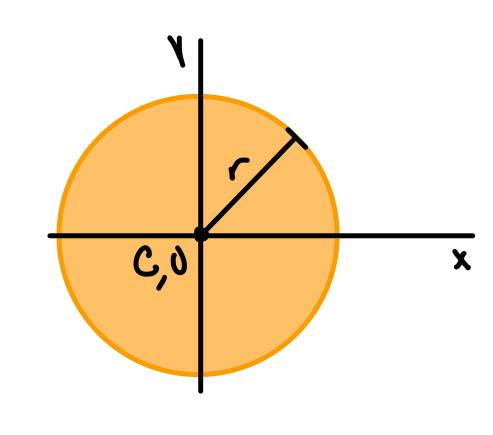
    		\( \bar{I_{x'}} = \bar{I_{y'}} = \frac{1}{4} \pi r^4 \)

    \( J_O= \frac{1}{2} \pi r^4 \)
    Semicircle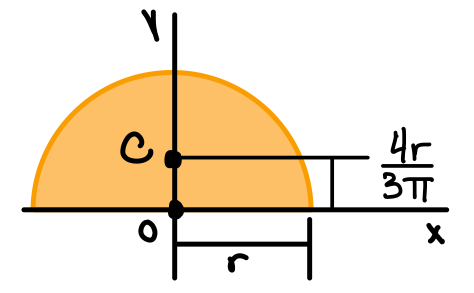
    		\( \bar{I_{x'}} = (\frac{\pi}{8} - \frac{8}{9\pi}) r^4 \)

    \( \bar{I_{y'}} = \frac{\pi}{8}r^4 \)    		\( I_x = I_y = \frac{1}{8} \pi r^4 \)

    \( J_O = \frac{1}{4} \pi r^4 \)
    Quarter circle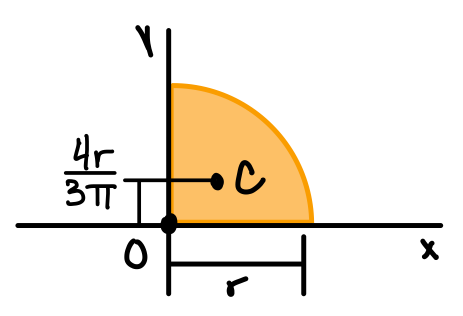
    		\( \bar{I_{x'}} = \bar{I_{y'}} = \frac{1}{2}(\frac{\pi}{8} - \frac{8}{9\pi}) r^4 \)\( I_x = I_y = \frac{1}{16} \pi r^4 \)

    \( J_O = \frac{1}{8} \pi r^4 \)
    Ellipse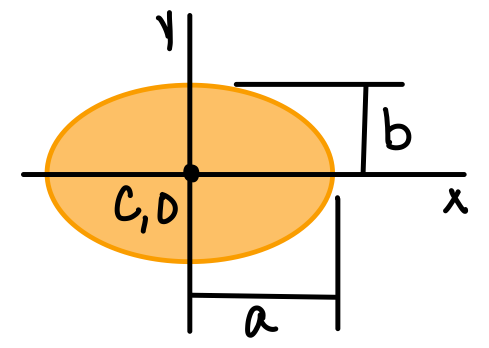
    		\( \bar{I_{x'}} = \frac{1}{4} \pi a b^3 \)

    \( \bar{I_{y'}} = \frac{1}{4} \pi a^3 b \)

    		\( J_O = \frac{1}{4} \pi ab(a^2+b^2) \)