Current page:

Stress

The internal forces and moments generally vary from point to point. Obtaining this distribution is of primary importance in mechanics of materials. The total force in a cross-section, divided by the cross-sectional area, is the stress. We use stress to normalize forces with respect to the size of the geometry.

Units

The units of stress can be found in the table below.

Measure	SI system	US system
Force	[$N$]	[$lb$]
Area	[$m^2$]	[$in^2$]
Stress	Pascal = [$Pa$] = [$N/m^2$]	pound per square inch = [$psi$] = [$lb/in^2$]

It is also important to recall some of the most common prefixes used to denote quantity.

kiloPascal [$kPa$]	$10^3$ [$Pa$]
megaPascal [$MPa$]	$10^6$ [$Pa$]
gigaPascal [$GPa$]	$10^9$ [$Pa$]

Typical sign convention for axial (normal) stress:

Tension:$ \sigma > 0 $
Compression:$ \sigma < 0 $

Stress under general loading conditions

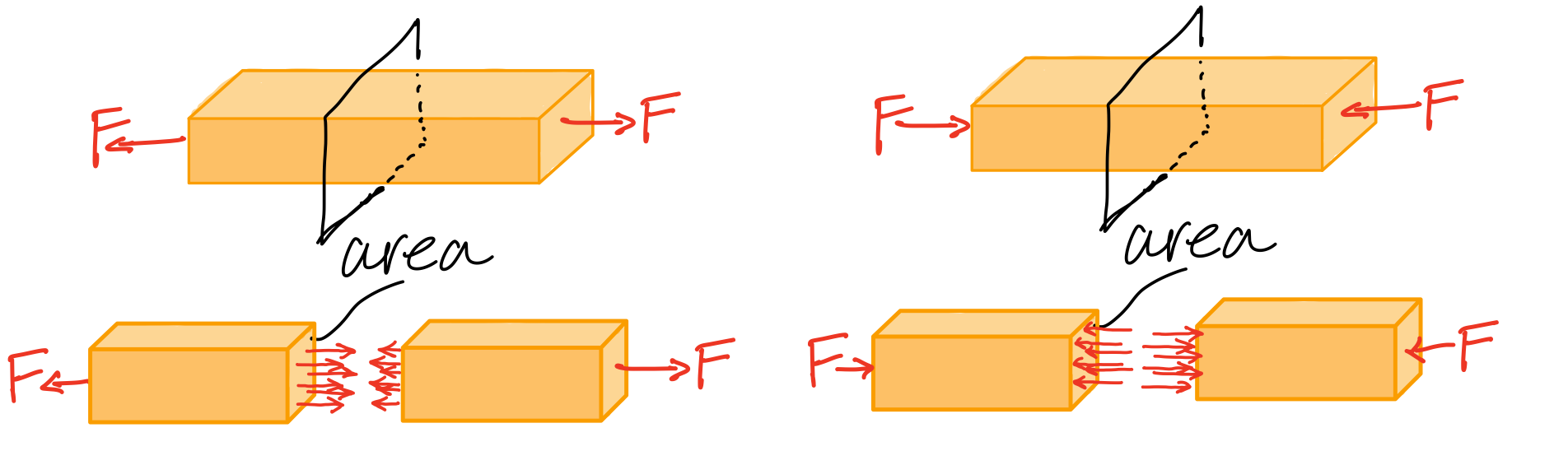
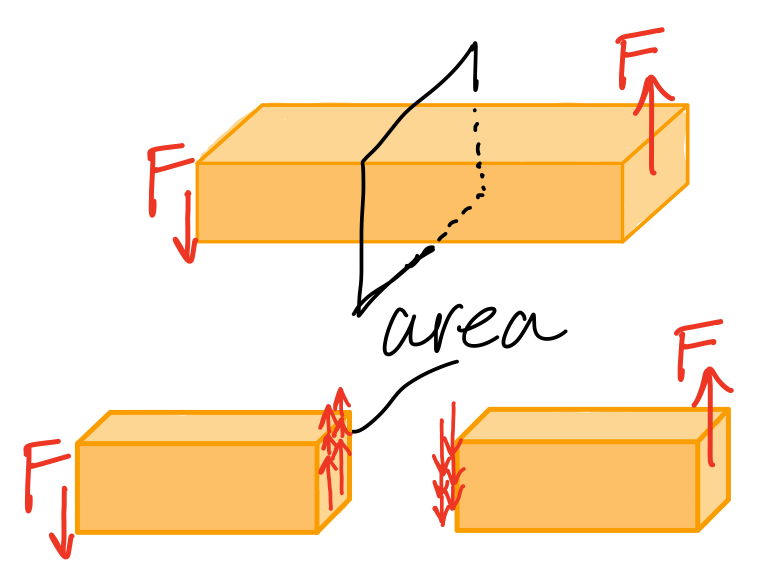
We consider a homogeneous distribution of the internal force $ \Delta F $ over an infinitesimal area $ \Delta A $. The stress is defined by the infinitesimal force divided by the infinitesimal area.

Normal Stress: Defined by the intensity of the force acting NORMAL to $ \Delta A $
Shear Stress: Defined by the intensity of the force acting TANGENT to $ \Delta A $

Average Normal Stress - Axial Loading

Normal stress

Here we assume that the distribution of normal stresses in an axially loaded member is uniform. Stress is calculated away from the points of application of the concentrated loads. Uniform distribution of stress is possible only if the line of action of the concentrated load $ P $ passes through the centroid of the section considered

Average normal stress. #avn-sts

$$ \sigma_{ave} = \frac{F}{A}\ $$

where $ F $ is the internal resultant normal force and $ A $ is the cross-sectional area of the bar where the normal stress $ \sigma_{ave} $ is calculated.

Non-uniform stress distribution

Around the point where the load is applied, the stress distribution is non-uniform. Cross-sections farther away from the point load gradually have a more uniform distribution. When the distance is greater than the widest dimension of the cross-section ($ l > b $), the stress distribution is uniform.

Average Shear Stress

Shear stress

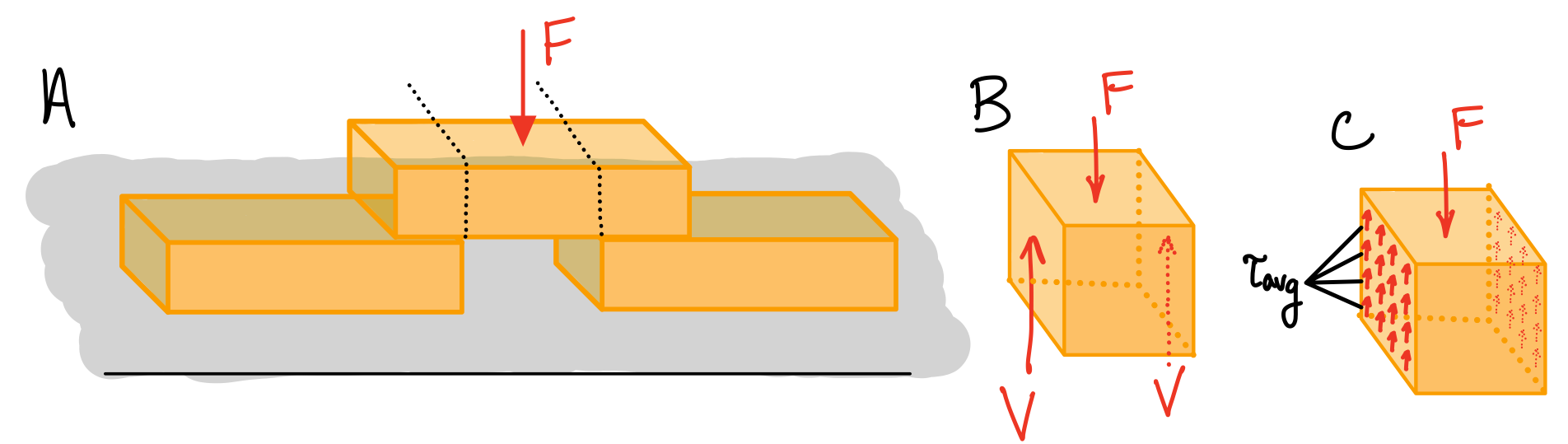
Obtained when transverse forces are applied to a member. The distribution of shear stresses cannot be assumed uniform. Common in bolts, pins and rivets used to connect various structural members.

Average shear stress

Average shear stress. #avs-sts

$$ \tau_{ave} = \frac{V}{A}\ $$

where $ V $ is the internal resultant shear force and $ A $ is the cross-sectional area of the bar where the shear stress $ \tau_{ave} $ is calculated.

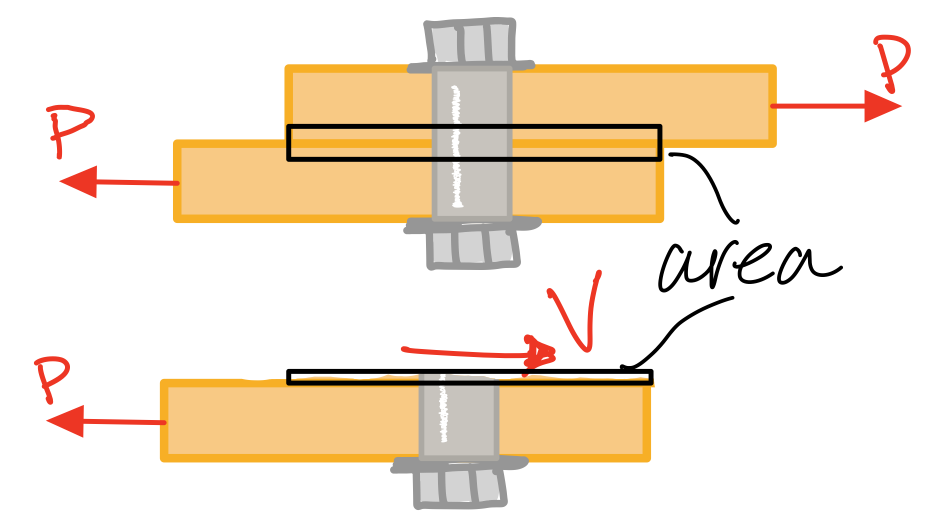
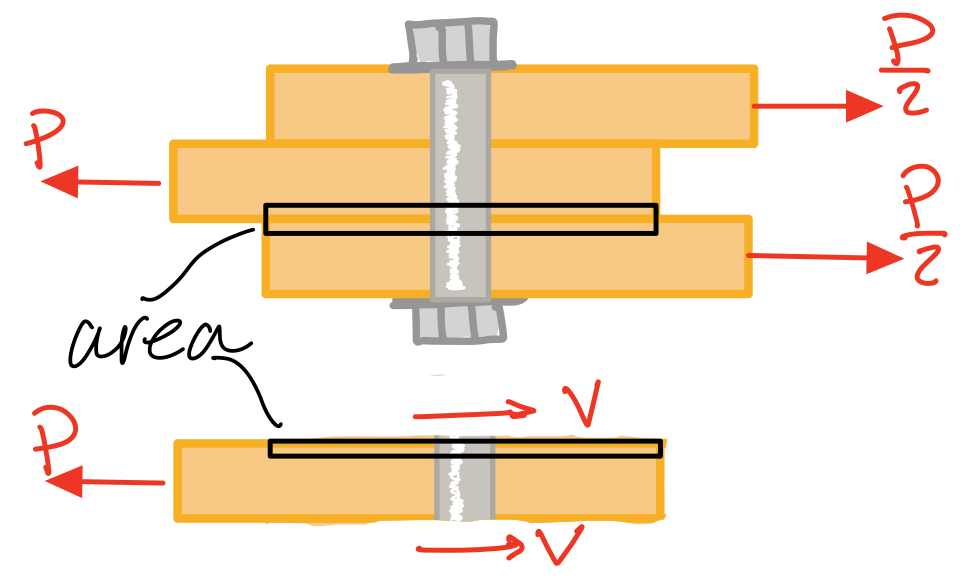
Example Problem: Single shear: determine the shear stress in the bolt #sgl-shr

Create the equilibrium equation and solve.

$$ \Sigma F_y = V-P = 0\ $$

$$ V = P\ $$

$$ \tau_{ave} = \frac{P}{A}\ $$

Example Problem: Double shear: determine the shear stress in the bolt #dbl-shr

Create the equilibrium equation and solve.

$$ \Sigma F_y = 2V-P = 0\ $$

$$ V = \frac{P}{2}\ $$

$$ \tau_{ave} = \frac{P}{2A}\ $$

Extra!

Supplemental video:

Stress Tensor

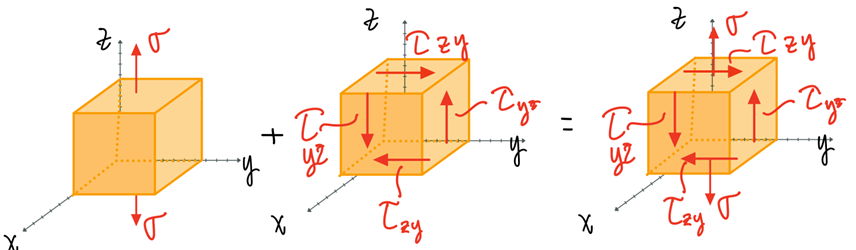
Stress element

The components of normal and shear stress can be combined into the stress tensor. This is a symmetric matrix representing the state of stress with respect to three directions.

Stress tensor.

$$ T= \begin{bmatrix} \sigma_{x} & \tau_{xy} & \tau_{xz} \\ \tau_{yx}& \sigma_{y} & \tau_{yz} \\ \tau_{zx}&\tau_{zy}&\sigma_{z} \end{bmatrix} \ $$

Three normal stress components: $ \sigma_x, \sigma_y, \sigma_z $
Six shear stress components: $ \tau_{xy} =\tau_{yx}, \tau_{xz}=\tau_{zx}, \tau_{yz}=\tau_{zy} $

The first subscript describes the surface orientation in the normal direction. The second subscript describes the direction of the stress.

Heads up!

Stress tensor builds on this content later in the course.

Learn more about this topic on the Stress Transformation page.

Support Reactions

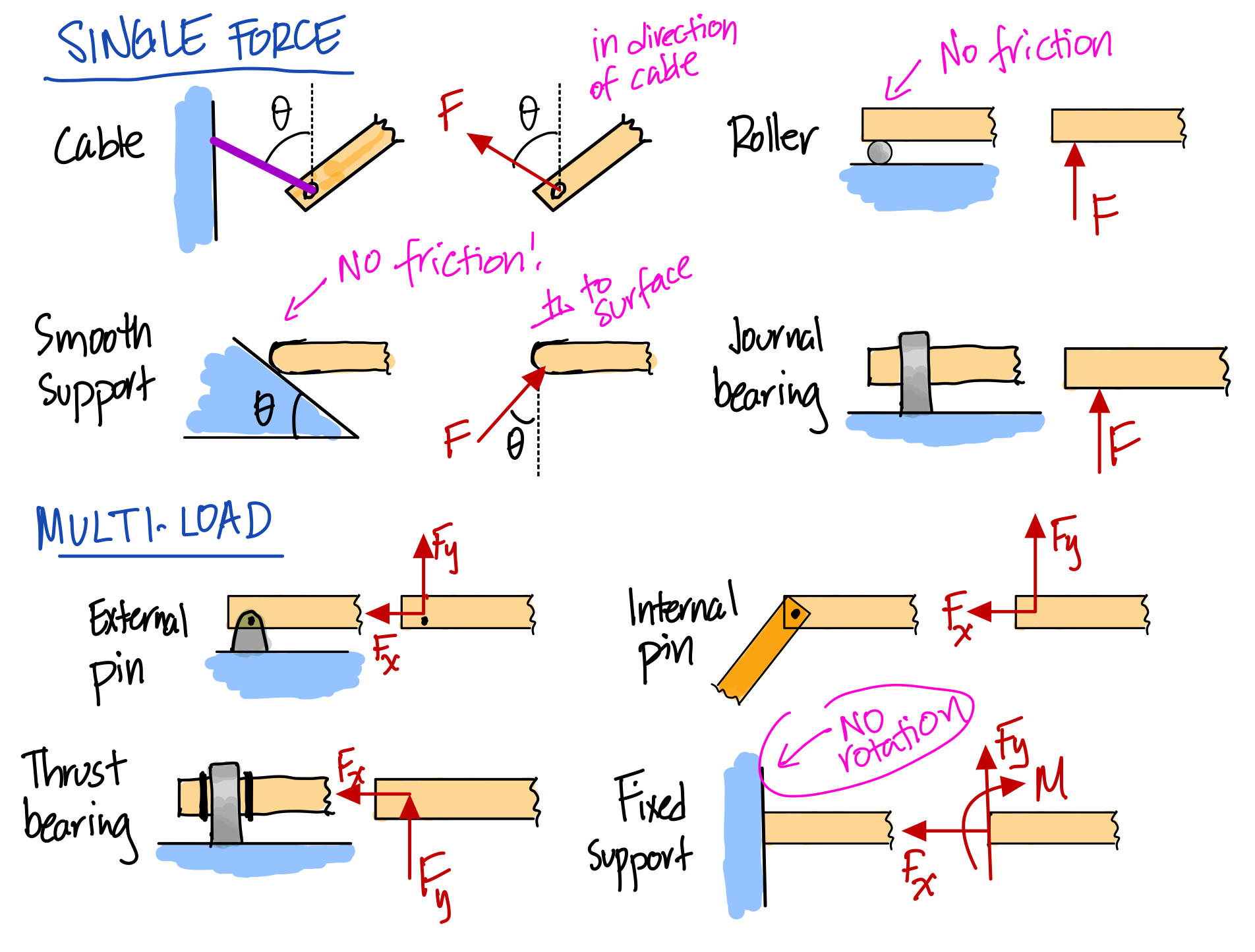
Support reactions

Allowable Strength Design

Design Requirement: A structural design is intended to support and/or transmit loads while maintaining safety and utility: don't break. Strength of a structure reflects its ability to resist failure.

Ultimate load ( $ P_u $ ): force when specimen fails (breaks).
Ultimate normal stress ( $ \sigma_u $ ): stress when a specimen fails (breaks).

Ultimate normal stress

$$ \sigma_u = \frac{P_u}{A}\ $$

A structure is safe if its strength exceeds the required strength.

Factor of Safety (FS): Ratio of structural strength to maximum (allowed) applied load ($ P_{all} $).

Maximum allowed applied load.

$$ P_{all} \le \frac{P_u}{FS}\ $$

Similarly,

Maximum allowed applied stress.

$$ \sigma_{all} \le \frac{\sigma_u}{FS}\ $$

kiloPascal [\(kPa\)]	\(10^3\) [\(Pa\)]
megaPascal [\(MPa\)]	\(10^6\) [\(Pa\)]
gigaPascal [\(GPa\)]	\(10^9\) [\(Pa\)]

Measure	SI system	US system
Force	[\(N\)]	[\(lb\)]
Area	[\(m^2\)]	[\(in^2\)]
Stress	Pascal = [\(Pa\)] = [\(N/m^2\)]	pound per square inch = [\(psi\)] = [\(lb/in^2\)]