Entropy
The Second Law: Energy dispersal
All energy spontaneously disperses if it is not prevented from doing so. This fact has been repeatedly deduced from observation and underlies the variety of ways of stating the second law of thermodynamics.
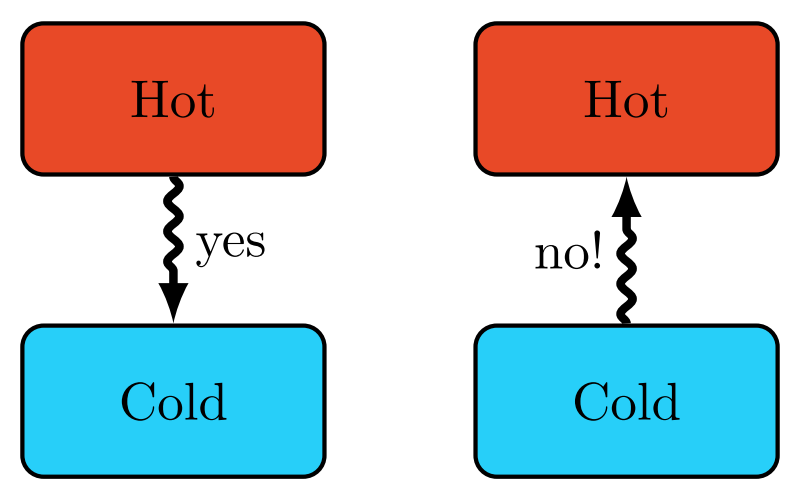
Clausius Statement of the Second Law
Heat spontaneously flows from a hot object to a colder object, but not the other way around. It is impossible for any system to operate in such a way that the sole result would be an energy transfer by heat from a cooler to a hotter body.
Expansion
A gas trapped in a rigid chamber will fill this container's volume. If this chamber is to expand, the gas will spontaneously expand to fill the entire chamber.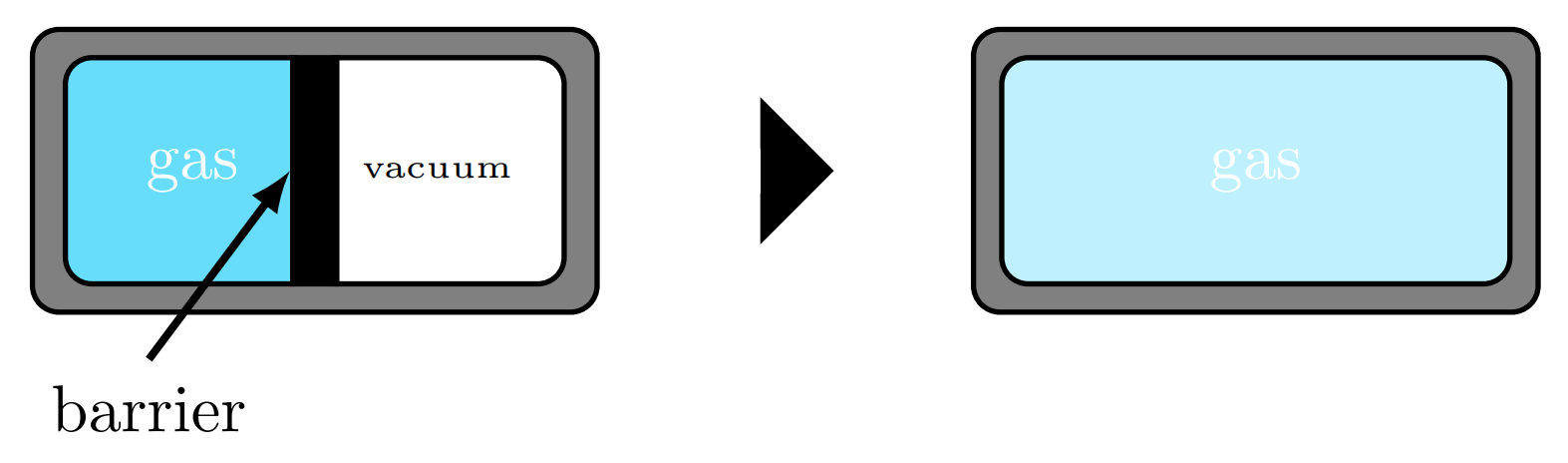
A closed system energy balance on the chamber illustrates that the gas experiences no energy change, i.e., because no heat transfer occurred and no work was done on or by the system.
Though the energy has not changed, the energy has spread out, or dispersed, within the chamber, meaning there aremore ways for the energy to exist in the chamber, or that the gas has more microstates available to it.
Directionality
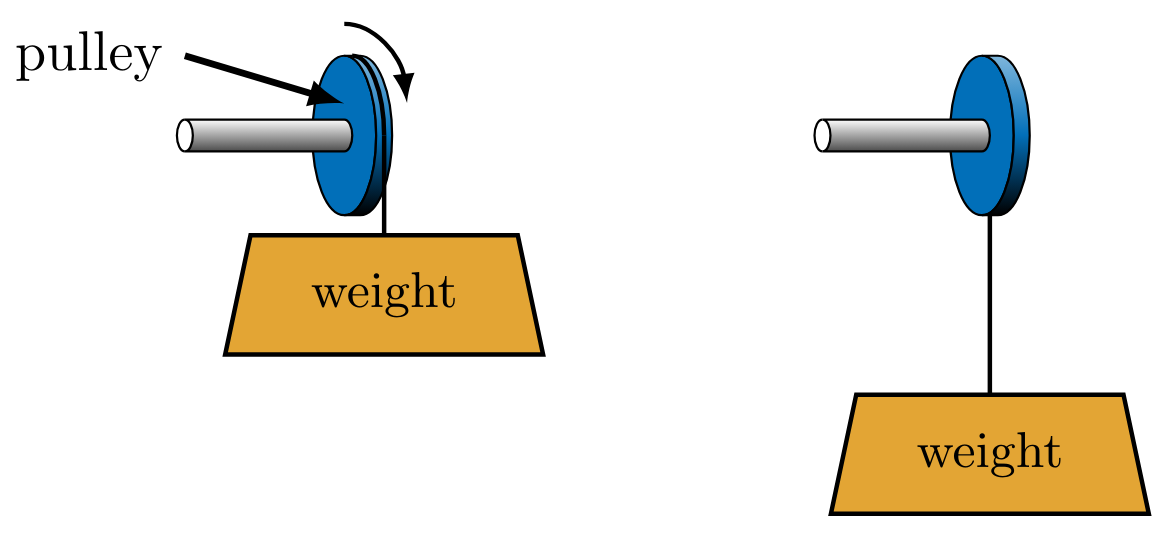
From observations of spontaneous processes, it is suggested that the second law restricts the directionality of processes. Spontaneous processes such as falling objects (Fig. WeightLower) and cooling frying pans are encountered every day. Spontaneous processes are irreversible, meaning that after they occur, the system and all parts of its surroundings cannot be exactly restored to their respective initial states. Auxiliary processes that can return the system to its initial state (i.e., raise the object or heat the pan), also change the state of the surroundings. These experiences suggest a directionality to processes that is formalized by the second law of thermodynamics.
Kelvin-Planck Statement of the Second Law
Statement:
It is impossible for any system to operate in a thermodynamic cycle and deliver a net amount of energy by work to its surroundings while receiving energy by heat transfer from a single thermal reservoir.
Any hypothetical system that violates either the first or the second laws of thermodynamics cannot be.Clausius Inequality
The Clausius inequality, a collary of the second law, states that for any thermodynamic cycle
where \( \delta Q \) is the heat transfer across some part of the system boundary for some portion of the cycle, and \( T \) is the absolute temperature at that part of the system boundary, of which we are reminded by the subscript `b`.
Reversible Process
- A cycle is reversible when the Clausius inequality becomes equality.
- In a reversible process, the system and all parts of its surroundings can be exactly restored to their respective initial states after the process has taken place.
- Such processes cannot occur in reality.
Internally Reversible Cycles
Internally reversible processes contain no irreversibilities within the system, but can interact with surroundings that include irreversibilities. Thus the validity of the equality holds, even in surroundings where irreversibilities occur.
What is Entropy?
For a reversible processes, the integral of \( \delta Q/T \) is path independent, and this thermodynamic property is called entropy.
- Entropy \( S \) is the measure of energy dispersal as a function of temperature.
- Entropy is a state function, with the state being determined by any two intensive thermodynamic properties.
- An entropy change for an incompressible substance depends only on temperature.
Differential form of the closed system energy balance
The differential form of the closed system energy balance for an internally reversible process on a simple, compressible system can be written as,
Specific Entropy of an Ideal Gas
For an ideal gas with a given, constant specific heat \( c_v \), its change in specific entropy from a state \( 1 \) to a state \( 2 \) is given by the expression
where \( R \) is the gas constant and \( v \) is the specific volume.
For an ideal gas with a given, constant specific heat \( c_p \), its change in specific entropy is given by the expression.
Differential form of the enthalpy equation
This differential equation of enthalpy and Eqn. fund are both known as fundamental equations of thermodynamics and relate thermodynamic properties between states. We use these expressions and the ideal gas as a model substance to gain some physical insight about entropy.
Entropy Balance
The closed system entropy statement of the second law derives from the Clausius Inequality which in turn derives from the Kelvin-Planck statement. As we have shown, this statement is
where \( \sigma \) represents the entropy produced in the system due to the irreversibilities (Fig. EntropyBal) in the process and the `b' indicates that the heat is transferred across a boundary having temperature \( T_b \). To satisfy the second law, \( \sigma \geq 0 \). Entropy production \( \sigma \) only equals zero when a process is reversible.
Entropy Balance and multiple heat transfer events
When boundary temperature is constant, and multiple, distinct heat transfers occur, Eqn. Centropy1 becomesRate of Change of Entropy
In the absence of mass flow, the rate of change of the entropy in a system is derived as
Microstates
The sets of possible configurations of the molecules are known as microstates and a state has a higher entropy when there are more microstates available to it.
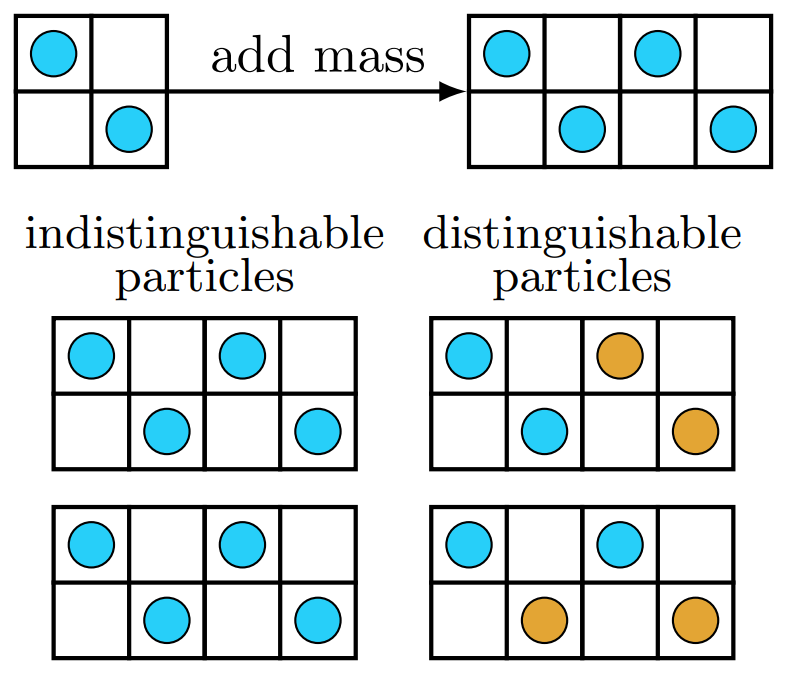
When adding mass to a system (as shown viaa two-dimensional gas of two particles in a volume, which is then doubled as shown at the top of Fig. Indistinguishable),
- If the added particles are identical to the original particles (indistinguishable). Therefore, the two `microstates' at the lower left are exactly the same even if the particles switch places, and this counts as only one microstate.
- On the other hand, for distinguishable particles, the two microstates are different. More microstates means higher entropy, thus when combining dissimilar materials there is a so-called entropy of mixing. (This course does not include entropy of mixing.)
- The addition of identical substances requires no entropy of mixing and therefore entropy of the new system increases in direct proportion to its increase in mass.
Principal of Superposition
Entropy added to a system thus follows a principal of superposition meaning that the total system entropy, \( S \), is the sum of the sub-system entropies.
where each subsystem `\( i \)` of mass \( m_i \) has specific entropy \( s_i \) relative to some universal reference state.
Open System Entropy Rate Balance
It follows that for an open system involving no mixing of substances, the entropy rate balance is simply