Current page:

Composite Thermodynamic Systems
Transient Systems
- Transient vs. Steady State Example

Solving complex systems

Composite Thermodynamic Systems

Before starting any problem, it is very helpful to familiarize yourself with the elements being addressed and any terminology being used. In approaching integrated, multi-device systems, following steps provide a framework that may avoid simple mistakes:

Identify known states - states are known in a simple, compressible system when two intensive thermodynamic properties are known.
Determine unknowns - stream states, energy flows, and mass flows are all potential unknowns.
Write energy balances - the number of unknowns must equal the number of mass and energy balances to solve a system.

Step 1: Identify Known States

The state principle is a guide to aid in determining the number of independent properties required to fix the state of a system. When the state of a system is known, it can be plotted as a single point on a $p v$ diagram. The state of a simple, compressible substance is considered known if at least two intensive properties are known. Recall that intensive properties are independent of the total mass of the substance, such as $v$ , $u$ , $h$ , $T$ , $p$ , and $x$ .

Step 2: Determine Unknowns

We next apply our knowledge of thermodynamic devices to identify other energy flows in the system that might not be given. Although the primary purpose of this class is tracking the flow of energy, the preliminary step before writing any energy balance should be to identify mass flow streams and write any mass balances.

Step 3: Write Energy Balances

After determining the necessary mass rate balances, we can write energy balances. Depending on the amount of unknown, as variables needing to be determined there are two approaches to writing energy balances.

Write an energy balance for each device where there is one system boundary around each device.
Write an energy rate balance for the entire composite system that includes all devices within the entire composite system.

The total possible equations are determined by the sum of the number of `devices` that possess at least one unknown value (energy balances) $N_{E}$ and the number of `devices` for which mass streams branch (mass balances) $N_{M}$ .

Total independent equations = N_{E} + N_{M}

Example: Refrigeration and Heat Pump Cycles

Refrigeration and heat pump cycles differ from a power cycle in $3$ ways: 1) heat is transferred from a cold reservoir to a hot reservoir, going in the opposite direction of spontaneous heat transfer, 2) there is a net power input to accomplish this task, and 3) performance is not quantified in terms of thermal efficiency $η$ since this performance measurement does not reflect the objective of these cycles. Performance is still quantified as

Performance #performance

Performance \equiv \frac{Required Output}{Necessary Input}

For a refrigeration cycle, the required output is heat removed from the cold environment and the necessary input is the net work input $| {\dot{W}}_{cycle} |$ . For a heat pump, the required output is the heat transferred to the hot environment. These performance measures are known as the coefficient of performance $β$ and $γ$ for a refrigeration cycle and heat pump cycle, respectively.

Refrigeration/heat pump cycle consists of the following types of thermal devices:

Throttle: expansion valve
Heat exchanger: evaporator and condenser
Compressor

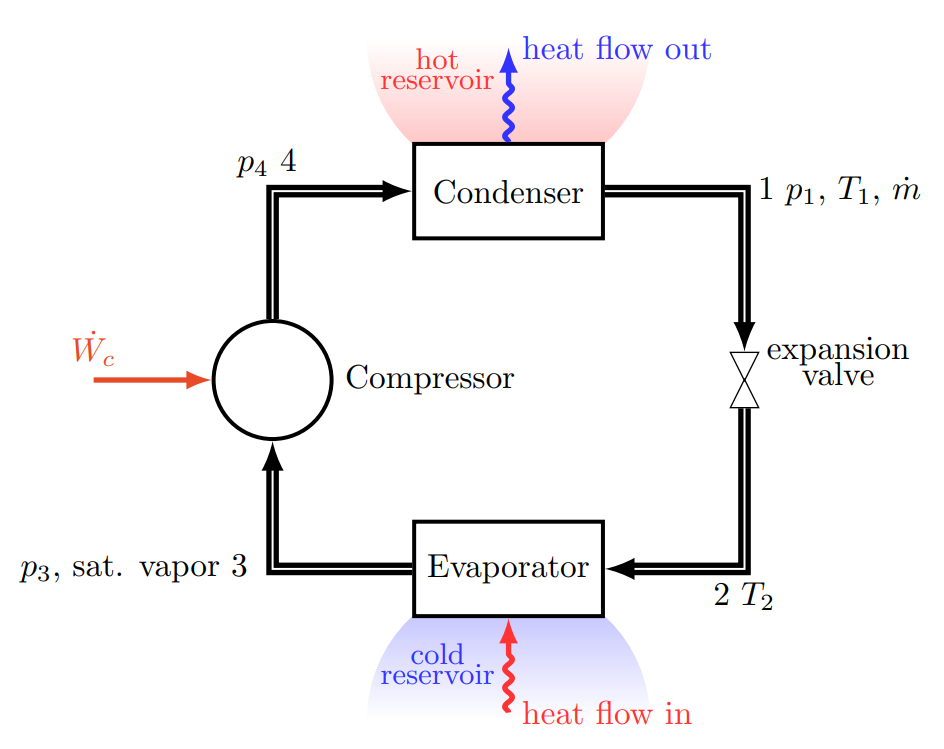
Figure 1: A schematic of a refrigeration cycle or heat pump cycle. All known properties and energy flows are represented with variables. Refrigerant is the working fluid.

Step 1: The streams that have known states are streams 1 and 3. Known energy flow in the cycle is the power input into the compressor, ${\dot{W}}_{c}$ .

Step 2: The unknowns for this cycle are streams 2 and 4, and heat flow in ( $Q_{in}$ ) and heat flow out ( $Q_{out}$ ).

Step 3a: The coefficient of performance of the refrigeration cycle, $β$ , requires $Q_{in}$ . To solve for $Q_{in}$ , we can define a combined system of evaporator and expansion valve (streams 1 and 3 are known). The energy balance for the combined evaporator and expansion valve system:

\begin{aligned} {\frac{d U}{d t}}^{0} & = \dot{Q} - {\dot{W}}^{0} + \sum {\dot{m}}_{in} h_{in} - \sum {\dot{m}}_{out} h_{out} \\ = {\dot{Q}}_{in} + \dot{m} (h_{1} - h_{3}) \\ {\dot{Q}}_{in} & = \dot{m} (h_{3} - h_{1}) \end{aligned}

The expression for the coefficient of performance, $β$ , as a function of $| {\dot{W}}_{c y c l e} |$ , the heat input, and the heat output that corresponds to a refrigeration cycle is therefore:

\begin{aligned} β & = \frac{required output}{necessary input} \\ = \frac{{\dot{Q}}_{in}}{{\dot{W}}_{c}} \\ = \frac{\dot{m} (h_{3} - h_{1})}{{\dot{W}}_{c}} \end{aligned}

Step 3b: For a heat pump cycle, the coefficient of performance, $γ$ , requires $Q_{out}$ . To solve for $Q_{out}$ , we can define a combined system of compressor and condenser (streams 3 and 1 are known). The energy balance for the combined compressor and condenser system:

\begin{aligned} {\frac{d U}{d t}}^{0} & = \dot{Q} - \dot{W} + \sum {\dot{m}}_{in} h_{in} - \sum {\dot{m}}_{out} h_{out} \\ = - {\dot{Q}}_{out} + {\dot{W}}_{c} + \dot{m} (h_{3} - h_{1}) \\ {\dot{Q}}_{out} & = {\dot{W}}_{c} + \dot{m} (h_{3} - h_{1}) \end{aligned}

The expression for the coefficient of performance $γ$ as a function of $| {\dot{W}}_{c y c l e} |$ , the heat input, and the heat output that corresponds to a heat pump cycle is therefore:

\begin{aligned} γ & = \frac{required output}{necessary input} \\ = \frac{{\dot{Q}}_{out}}{{\dot{W}}_{c}} \\ = \frac{{\dot{W}}_{c} + \dot{m} (h_{3} - h_{1})}{{\dot{W}}_{c}} \\ = 1 + \frac{\dot{m} (h_{3} - h_{1})}{{\dot{W}}_{c}} \end{aligned}

Transient Systems

A transient system is a system in which the time derivative related to the system gain or loss (such as mass or energy) is not zero, which is the opposite of a steady state system.

Transient Systems:

Mass Flow

\frac{d m}{d t} (t) \neq 0

Energy Flow

\frac{d E}{d t} (t) \neq 0

Transient vs. Steady State Example

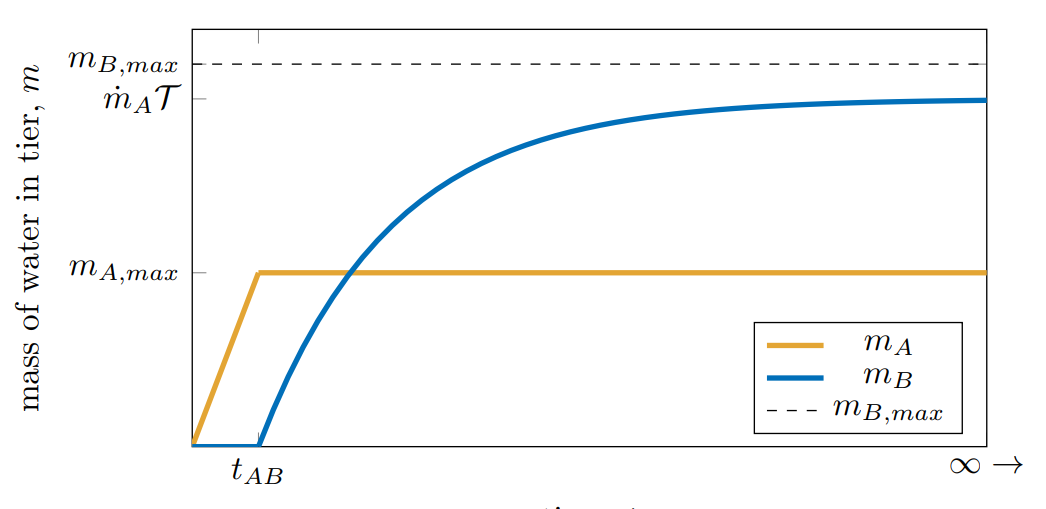
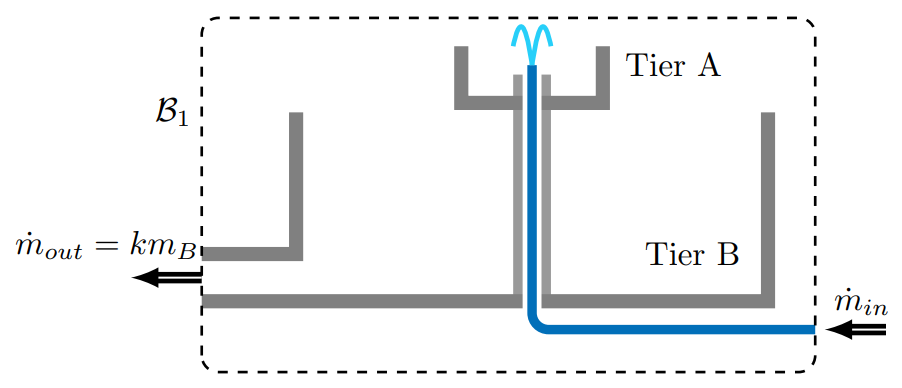
Imagine a two-tiered water fountain as depicted below. The maximum mass capacities of tier A and tier B are $m_{A, m a x}$ and $m_{B, m a x}$ , respectively. Once the mass in the tier crosses its threshold, water will overflow the tier. The inlet mass flow rate is a constant given by ${\dot{m}}_{i n}$ . However, the outlet flow rate is proportional to the amount of material in tier B, written as ${\dot{m}}_{o u t} = m_{B} (t) / T$ , where $1 / T$ is a proportionality constant with units of inverse time and $m_{B} (t)$ is the mass of the fluid in tier B at time $t$ . We can fully describe the fountain's operation at a variety of time points and conditions using the mass balance expressions.

Figure 2: A two-tiered water fountain.

Steady-State:

Drawing a system boundary, $B_{1}$ , around the entire fountain and considering when the fountain might be operating in steady-state (The diagonal arrow with the `ss' label indicates that this term is eliminated due to a `steady-state' assumption), Eqn. MassBalanceDiff, simplifies to,

\begin{aligned} {\frac{d m}{d t} (t)}^{s s} & = {\dot{m}}_{i n} - {\dot{m}}_{o u t} (t) \\ 0 & = {\dot{m}}_{i n} - m_{B} (t) / T \end{aligned}

from which it is clear that the fountain will operate at steady state whenever

Steady state mass-balance #SS_mB

m_{B} = {\dot{m}}_{i n} T .

Figure 3: A block diagram depicting mass flow in the two tier water fountain.

Transient System:

If it rains, an additional mass flow rate ${\dot{m}}_{r a i n}$ into the fountain must also be considered. Eqn. MassBalanceDiff then becomes

0 = {\dot{m}}_{i n} + {\dot{m}}_{r a i n} - m_{B} (t) / T,

from which we conclude that steady state occurs when $m_{B} = T ({\dot{m}}_{i n} + {\dot{m}}_{r a i n})$ . The fountain will overflow when the mass of water in Tier B is larger than its maximum allowable volume, or when $m_{B} > m_{B, m a x}$ . Combining these relations, we determine that the fountain will overflow from rain when

{\dot{m}}_{r a i n} > \frac{m_{B, m a x}}{T} - {\dot{m}}_{i n} .

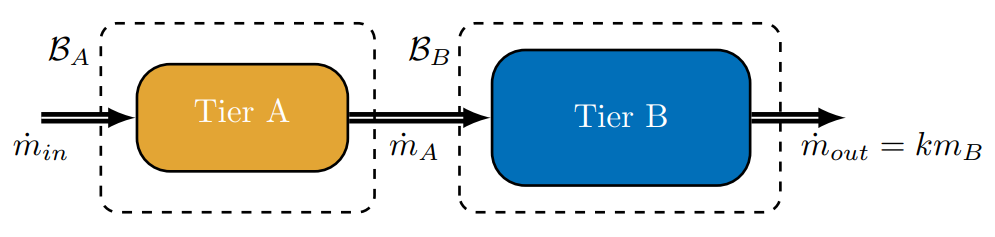
Similarly, overflow might occur when the timescale $T$ is increased, for example due to debris blocking the outlet pipe from Tier B even in the absence of rain. This scenario occurs when

T > \frac{m_{B, m a x}}{{\dot{m}}_{i n}} .

We model the transient process of turning on the fountain from an initially empty state ( $m_{A} (0) = m_{B} (0) = 0$ ), by first re-drawing our system in a way that clarifies system boundaries and mass flows.

First, Tier A will fill. Drawing our system boundary around the Tier A block above ( $B_{A}$ ) and using Eqn. MassBalanceInt we obtain the following expression for the mass in Tier A,

m_{A} (t) = m_{A} (0) + \int_{0}^{t} ({\dot{m}}_{i n} - 0) d τ = m_{i n} t .

Thus, the mass in Tier A increases linearly with time in proportion to the inlet flow rate. Tier A reaches it's capacity when $m_{A} (t) = m_{A, m a x} = {\dot{m}}_{i n} t$ or at time $t_{A B} = m_{A, m a x} / {\dot{m}}_{i n}$ . Afterward, Tier A is in steady-state, ${\dot{m}}_{A} = {\dot{m}}_{i n}$ , and flow enters Tier B.

Drawing our system boundary around the Tier B block above ( $B_{B}$ ) and using Eqn. MassBalanceDiff we obtain the following expression for the mass in Tier B for $t > t_{A B}$ as,

\frac{d m_{B}}{d t} (t) = {\dot{m}}_{A} - \frac{m F_{B} (t)}{T} .

It follows that the solution to this first-order, linear differential equation is

m_{B} (t) = m_{B} (0) e^{- t T} + T {\dot{m}}_{A} (- e^{- t / T}) = T {\dot{m}}_{i n} (1 - e^{- t T})

As $t \to \infty$ , the mass $m_{B} (t)$ asymptotically converges to ${\dot{m}}_{A} T$ , just as we found in our earlier steady state solution (Eq. SS_mB). These results are summarized in Figure FountainPlot.

Figure 4: A plot of the transient response of the water fountain in both tiers assuming that Tier B does not overflow.