Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Virtual Work

    In general, a force does work when it produces a displacement along its line of action. When we talk about virtual work, we're imagining those displacements becoming infinitesimally small.

    Work is defined as positive when the force and the displacement are in the same direction, and negative when the force and displacement are in opposite directions.

    Virtual work (\( dU \)) is the work produced by a force (\( F \)) over an infinitesimally small displacement (\( dr \)).
    Virtual work.
    $$ dU = F\cdot dr\ $$

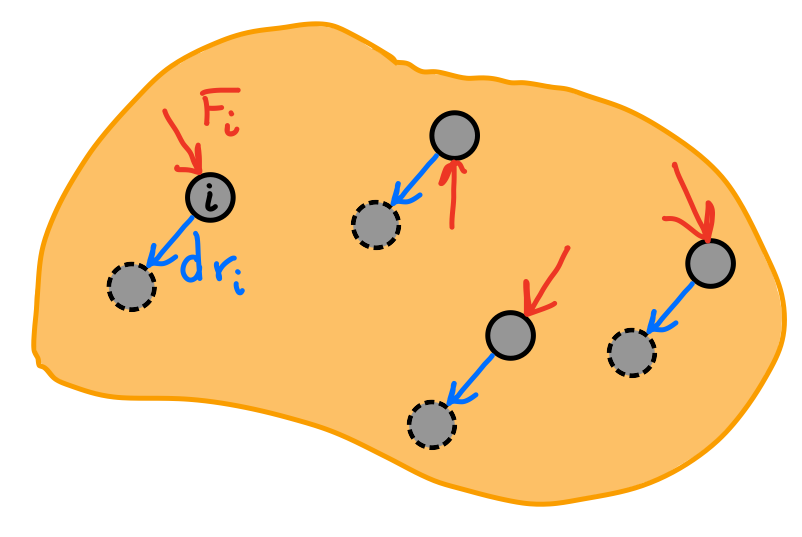
    Virtual Displacements

    A virtual displacement is an infinitesimally small translation (\( dr \)) and/or rotation (\( d\theta \)) that is possible in the system.


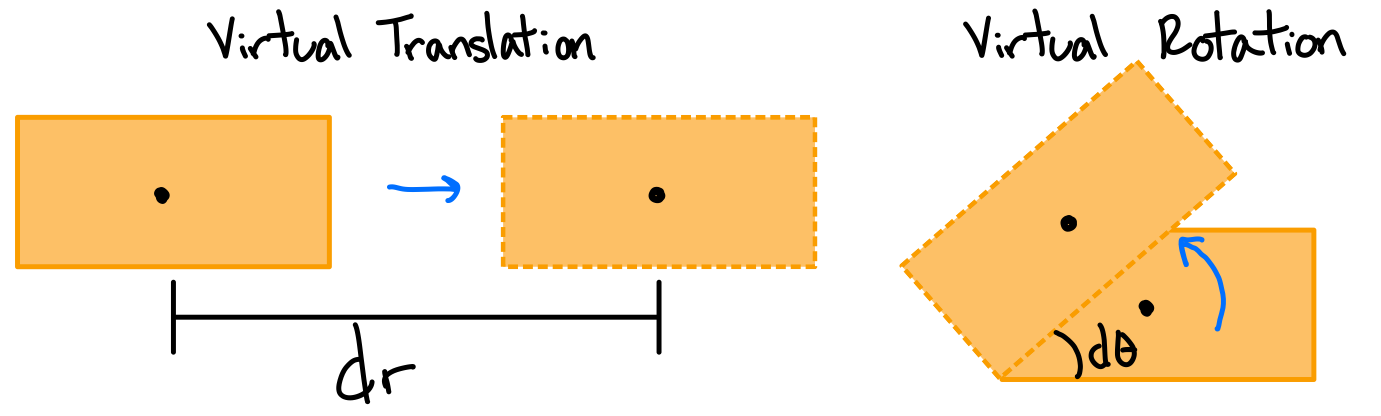
    Note: virtual displacements are assumed to be possible, but don't actually exist.

    Couple Moments

    Couple moments can also do work! When a body's rotation and the moment vector are oriented in the same direction, the couple moment does work. For 2D problems, this is when both the moment and the rotation are oriented in the \( \hat{k} \) direction using the right hand rule.

    In the example above, the orange shape both translates over a distance \( dr \) AND rotates about point A by an angle \( d\theta \). This rotation is caused by the couple moment from the force couple.

    Couple moment virtual work (\( dU \)) is the work produced by a couple moment (\( M \)) over an infinitesimally small angular displacement (\( d\theta \)).

    Virtual work of a couple moment. #cpl-mmt
    $$ dU = \vec{M} \cdot d\theta \hat{k} $$
    $$ dU = \Sigma \vec{F_i} \cdot d\vec{r_i} $$
    $$ dU = \vec{F_A} \cdot d\vec{r_A} +\vec{F_B} \cdot d\vec{r_B} $$
    $$ dU = -\vec{F} \cdot (d\vec{r_A} + d\theta \vec{k} \times \vec{r_{AA}}) + F \cdot (d\vec{r_A} + d\theta \vec{k} \times \vec{r_{AB}}) $$
    $$ d\theta \vec{k} \times \vec{r_{AA}} = 0 $$
    $$ dU = -\vec{F} \cdot d\vec{r_A} + \vec{F} \cdot d\vec{r_A} + \vec{F} \cdot (d\theta \vec{k} \times \vec{r_{AB}}) $$
    $$ dU = \vec{F} \cdot (d\theta \vec{k} \times \vec{r_{AB}}) $$
    $$ dU = d\theta \vec{k} \cdot (\vec{r_{AB}} \times \vec{F}) $$
    $$ dU = d\theta \vec{k} \cdot \vec{M} $$
    $$ dU = M \vec{k} \cdot d\theta \vec{k} $$

    Principle of Virtual Work

    If a body is in equilibrium, the sum of the virtual work done by all the forces and couple moments acting on the body is zero. We can use this principle to solve for the forces on systems.
    Virtual work equilibrium.
    $$ \sum{dU} = \sum{\vec{F}d\vec{x}} + \sum{\vec{M}d\vec{\theta}} = 0 $$

    Virtual Work Analysis

    Steps for completing an analysis of a system using virtual work:

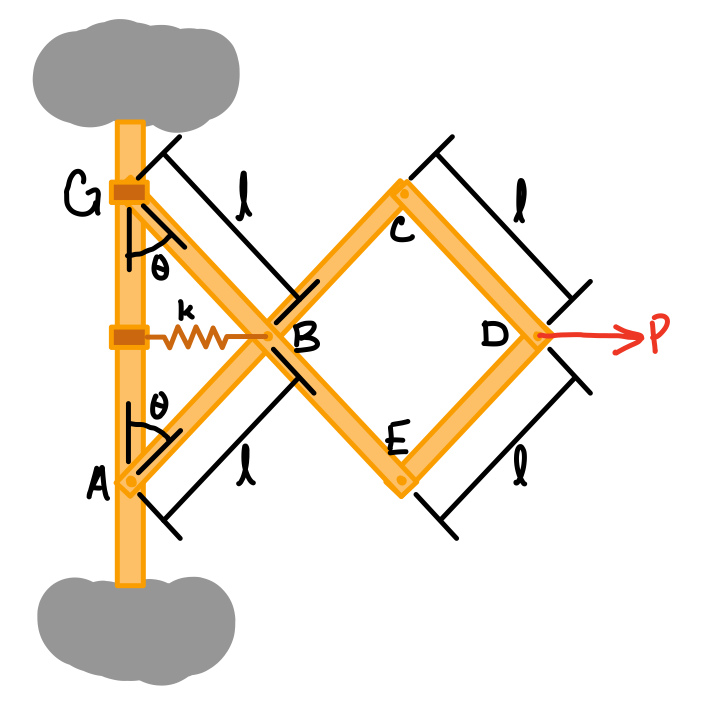
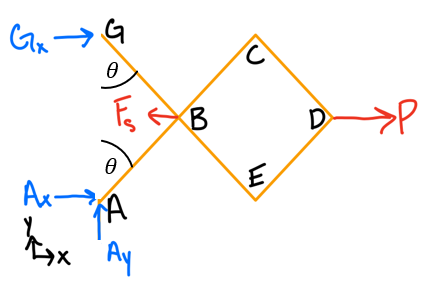
    1. Draw a free body diagram of the system, including a coordinate system.
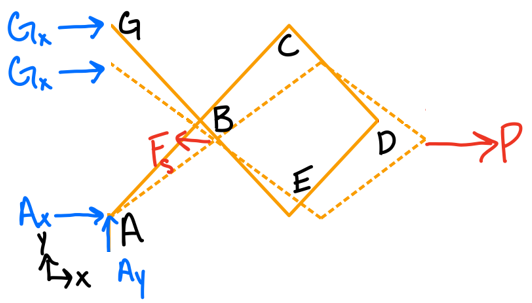
    2. Sketch the "deflected" position of the system.
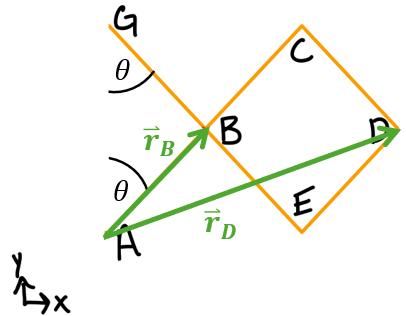
    3. Define the position coordinates (measured from a fixed point).
    4. Identify the components of the forces or moments that are parallel to the virtual displacements (the parallel line of action components).
    5. Remove all the forces that do not complete any work.
    6. Differentiate the position coordinates to obtain virtual displacement.
    7. Write the virtual work equation, expressing the virtual work of every force and moment.
    8. Factor out the common virtual displacement term (\( dr \) and/or \( dr \)) and solve.

    We can use virtual work to solve for the forces in a system without needing to solve for all of the support reactions.

    For example, if a truss is completely pinned on one end, it doesn't move, which means there is no virtual work completed on that pin because there are no virtual displacements (\( dr = 0 \)). This means that we can ignore it in our virtual work equation and don't need to solve for the reaction forces at the truss pin.

    Example Problem: Virtual work problem: box on a structure. #pin-trs

    The box has a mass of 10 kg. Determine the couple moment \( M \) needed to maintain equilibrium at \( \theta=60\deg \).

    1. Draw the free body diagram of the structure.
    2. Sketch the deflected position.
    3. Define the position coordinates from a fixed point. In this case, we are defining them from the fixed point B.
      4. $$ \vec{r_W} = (l cos\theta + 0.2)\hat{i} + (l sin\theta+b)\hat{j} $$
    4. Select the components of the forces that are parallel to the displacements. For this problem, only W and M have components parallel to any virtual displacement.
    5. Remove forces that do no work. \( B_x, B_y, D_x, D_y \) do not do any work (\( dU = 0 \)), so they can be removed.
    6. Differentiate the position coordinates.
      7. $$ d\vec{r_W} = (-l sin\theta \text{ } d\theta)\hat{i} + (l cos\theta \text{ } d\theta)\hat{j} $$
    7. Apply the Principle of Virtual Work.
      8. $$ \Sigma dU = M \text{ } d\theta + \vec{W} \cdot d\vec{r_W} = 0 $$
    8. Solve for \( M \).
      9. $$ \Sigma dU = M \text{ } d\theta + (-W \hat{j}) \cdot (-l sin\theta \text{ } d\theta \hat{i} + lcos\theta \text{ } d\theta \hat{j}) = 0 $$

    \( (-W \hat{j}) \cdot (-l sin\theta \text{ } d\theta \hat{i}) \) is zero, so we are left with:
    $$ \Sigma dU = M \text{ } d\theta -Wl cos\theta \text{ } d\theta = 0 $$
    Factor out \( d\theta \):
    $$ (M - Wlcos\theta)\text{ }d\theta = 0 $$
    $$ M = Wlcos\theta $$
    Example Problem: Rod leaning against a wall. #rod-wal

    A thin rod with a weight \( W \) rests against a smooth wall and floor. Determine the magnitude of force \( P \) needed to maintain equailibrium.

    1. Draw the free body diagram.
    2. Sketch the deflected position.
    3. Define the position coordinates from a fixed point. In this case, we will use the fixed point of the origin at the corner of the wall and floor as our fixed point.
      4. Point A:
      $$ \vec{r_A} = -Lcos\theta\hat{i} $$
      Point B:
      $$ \vec{r_B} = Lsin\theta \hat{j} $$
      COM:
      $$ \vec{r_W} = -\frac{L}{2} cos\theta \hat{i} + \frac{L}{2}sin\theta\hat{j} $$
    4. Identify forces that have components parallel to the virtual displacements. For this problem, this would only be the weight \( W \).
    5. Remove forces that do no work. \( N_a, N_b \) do not do any work (\( dU = 0 \)), so they can be removed.
    6. Differentiate the position coordinates.
      7. Point A:
      $$ d\vec{r_A} = Lsin\theta \text{ } d\theta \hat{i} $$
      Point B:
      $$ d\vec{r_B} = Lcos\theta \text{ } d\theta \hat{j} $$
      COM:
      $$ d\vec{r_W} = \frac{L}{2} sin\theta \text{ } d\theta \hat{i} + \frac{L}{2}cos\theta \text{ } d\theta \hat{j} $$
    7. Apply the Principle of Virtual Work.
      8. $$ \Sigma dU = \Sigma \vec{F} \cdot d\vec{r} = 0 $$
    8. Solve by factoring out the common virtual displacement term (in this case, \( d\theta \)).
      9. $$ \Sigma dU = \vec{P} \cdot d\vec{r_A} + \vec{W} \cdot d\vec{r_W} = 0 $$
      $$ \Sigma dU = (P\hat{i}) \cdot (L sin\theta \text{ } d\theta \hat{i}) - (W\hat{j}) \cdot (\frac{L}{2} sin\theta \text{ } d\theta \hat{i} + \frac{L}{2}cos\theta \text{ } d\theta \hat{j}) = 0 $$
      $$ \Sigma dU = PLsin\theta\text{ } d\theta - \frac{WL}{2}cos\theta \text{ } d\theta = 0 $$
      $$ \Sigma dU = L \text{ } d\theta(Psin\theta - \frac{W}{2}cos\theta) = 0 $$
      $$ Psin\theta - \frac{W}{2} cos\theta = 0 $$
      $$ P = \frac{Wcos\theta}{2sin\theta} $$

    Warning: Virtual work can be an easier method of solving for some problems. #vrt-wrk

    For simple problems, virtual work is about the same amount of work as the equilibrium equations.