Material Properties
Stress-Strain Diagram
A stress-strain diagram is the relationship of normal stress as a function of normal strain. One way to collect these measurement is a uniaxial tension test in which a specimen at a very slow, constant rate (quasi-static). A load \( P \) and distance \( L \) are measured at frequent intervals.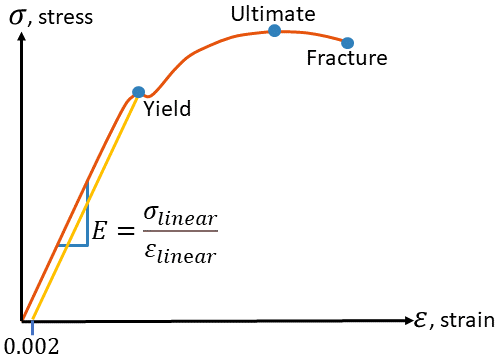
Elastic Behavior
Loading in this region results elastic behavior, meaning the material returns to its original shape when unloaded. This region of the diagram is mostly a straight line, limited by the proportional limit). This region ends at \( \sigma_Y \) (yielding). For \( \sigma \le \sigma_{pl} \), the diagram is linear, and the behavior is elastic. For \( \sigma_{pl} < \sigma < \sigma_Y \), the diagram is nonlinear, but the behavior is still elastic. Young's Modulus Hooke's law is used for small deformations in the elastic region. The Young's modulus is the slope \( E \).| Material | Young's modulus [\(GPa\)] |
|---|---|
| Mild Steel | 210 |
| Copper | 120 |
| Bone | 18 |
| Plastic | 2 |
| Rubber | 0.02 |
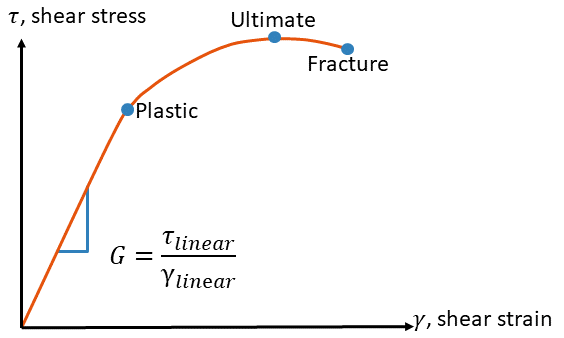
Plastic Behavior
Stresses above the plastic limit (\( \sigma_Y < \sigma \)) cause the material to permanently deform.Yield Strength
Perfect plastic or ideal plastic: well-defined \( \sigma_Y \), stress plateau up to failure. Some materials (e.g. mild steel) have two yield points (stress plateau at \( \sigma_{YL} \)). Most ductile metals do not have a stress plateau; yield strength \( \sigma_{YS} \) is then defined by the 0.002 (0.2%) offset method.
Strain Hardening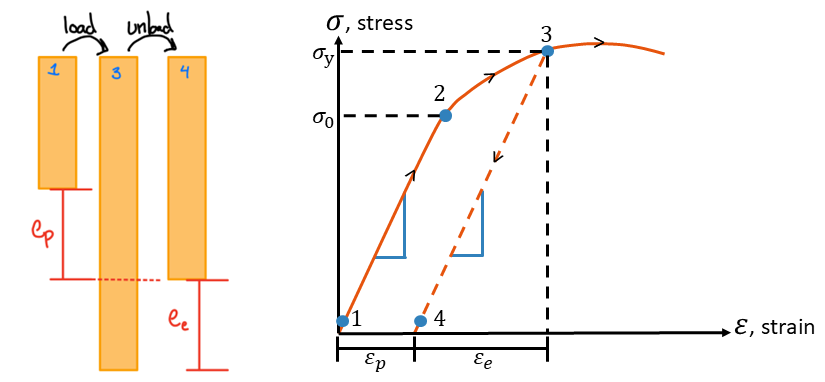
Atoms rearrange in plastic region of ductile materials when a higher stress is sustained. Plastic strain remains after unloading as permanent set, resulting in permanent deformation. Reloading is linear elastic up to the new, higher yield stress (at A') and a reduced ductility.
Ultimate StrengthThe ultimate strength (\( \sigma_u \)) is the maximum stress the material can withstand.
Necking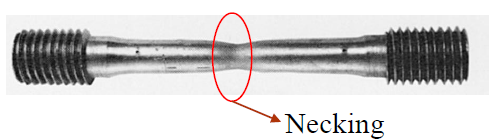
After ultimate stress (\( \sigma_u < \sigma \)), the middle of the material elongates before failure.
FailureAlso called fracture or rupture stress (\( \sigma_f \)) is the stress at the point of failure for the material. Brittle and Ductile materials fail differently.
Ductile materials generally fail in shear. There is a large region of plastic deformation before failure (fracture) at higher strain and necking.

Brittle materials are weaker in tension than shear. There is a small plastic region between yield and failure (fracture) and no necking.

Note the difference between engineering and true stress/strain diagrams: ultimate stress is a consequence of necking, and the true maximum is the true fracture stress.
Example: Concrete is a brittle material.- Maximum compressive strength is substantially larger than the maximum tensile strength.
- For this reason, concrete is almost always reinforced with steel bars or rods whenever it is designed to support tensile loads.
Heads up!
Strain Energy builds on this content in Engineering Materals.
Deformation does work on the material: equal to internal strain energy (by energy conservation).
Heads up!
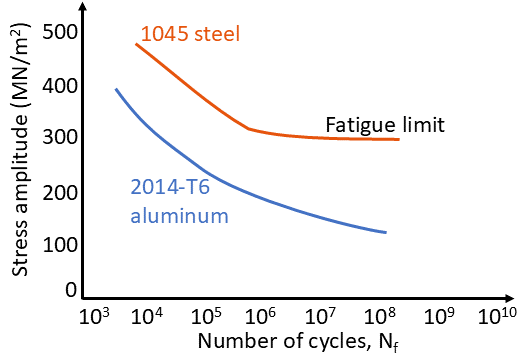
Fatigue builds on this content in Engineering Materals and Mechanical Design.
Directional Materials
- Isotropic: material properties are independent of the direction
- Anisotropic: material properties depend on the direction (ie; composites, wood, and tissues)
Poisson's Ratio
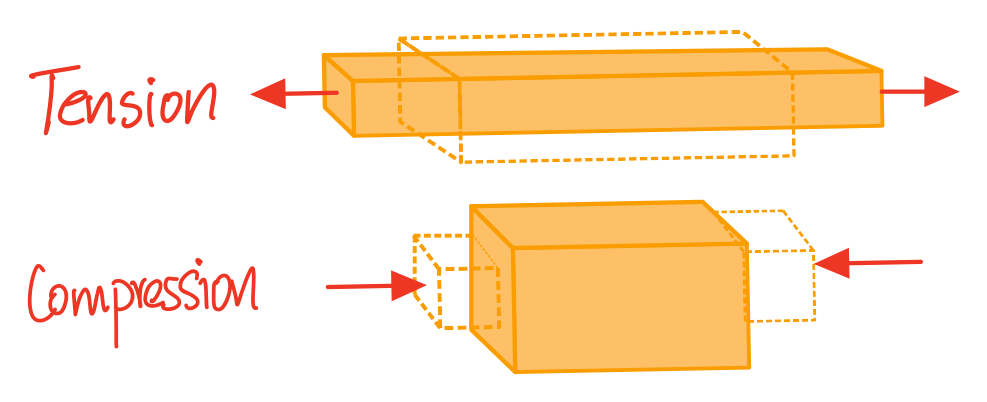
As illustrated in the figure above, when an object is being compressed it expands outward, and when stretched it will become thinner. Depending on the material, it may experience more or less lateral deformation for a given amount of axial deformation. The ratio that governs the amount of lateral strain per unit of axial strain is called Poisson's ratio.