Failure Theories

Failure of a material depends on (1) nature of loading and (2) type of material. There are theories that can predict material failure for complex states.

Maximum Shear Stress (Tresca) Criterion

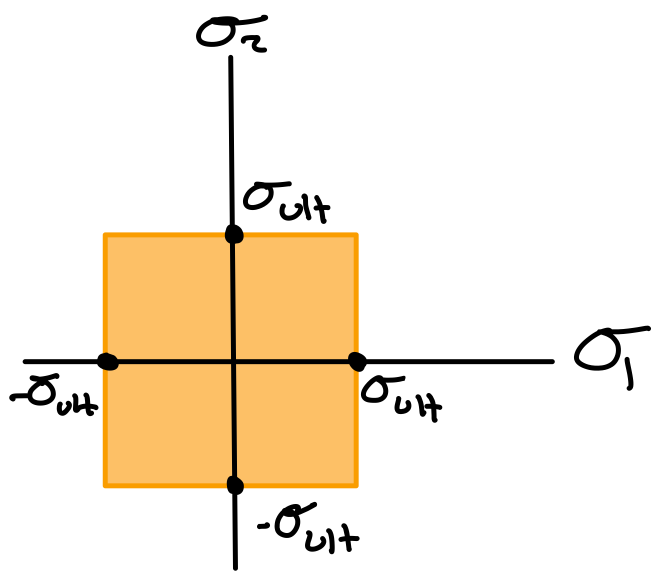
If a material is ductile, failure is defined by yield stress ($ \sigma_Y $) and occurs at max shear stress ($ \tau_{max} $).

Uniaxial Tension

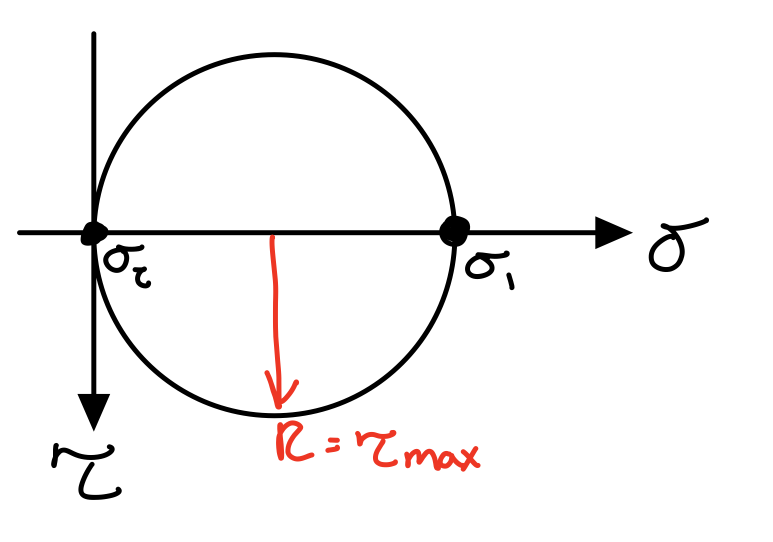
Consider a material subjected to uniaxial tension $ \sigma = \frac{P}{A} $ and $ P $ is loaded to the yield point, then the following is true:

Tresca uniaxial tension.

$$ \begin{align} \sigma_1 = \sigma_Y \\ \sigma_2 = 0 \\ \tau_{max} = \frac{\sigma_Y}{2} \end{align} $$

Shear stress is responsible for causing the ductile material to yield and $ \sigma_Y $ is the tensile yield strength.

Max shear.

$$ \tau_{max} \ge \frac{\sigma_Y}{2}\ $$

General 2D Loading State

Plane stresses.

$$ \sigma_z = \sigma_3 = 0\ $$

Failure still occurs at max shear.

Tresca material failure.

$$ \tau_{max} = \frac{\sigma_Y}{2}\ $$

The equations for $ \sigma_1 $ and $ \sigma_2 $ can be plotted to show the failure surface. Loading conditions that occur outside of the surface are when the material fails.

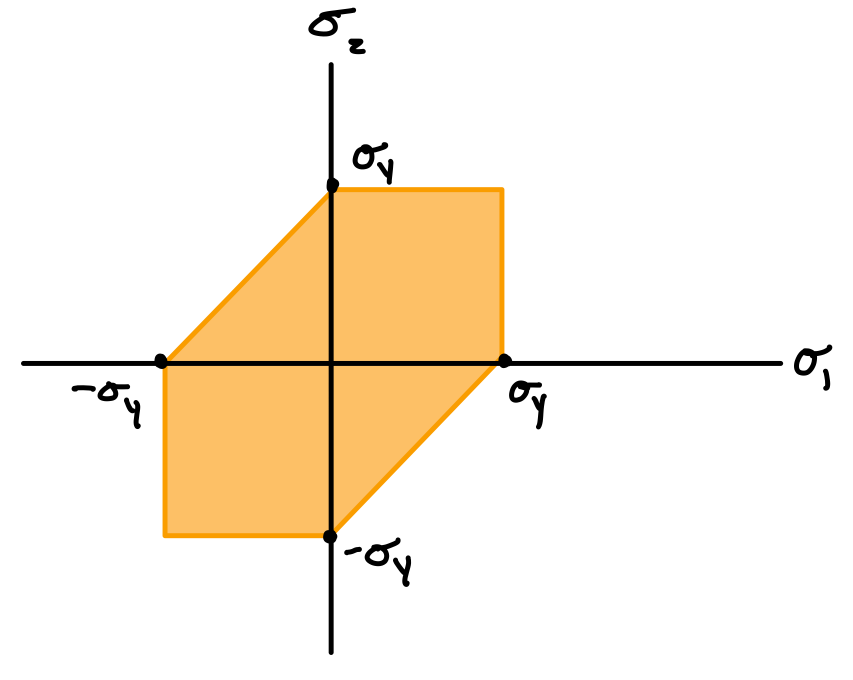
If $ \sigma_1 $ and $ \sigma_2 $ have the same signs:

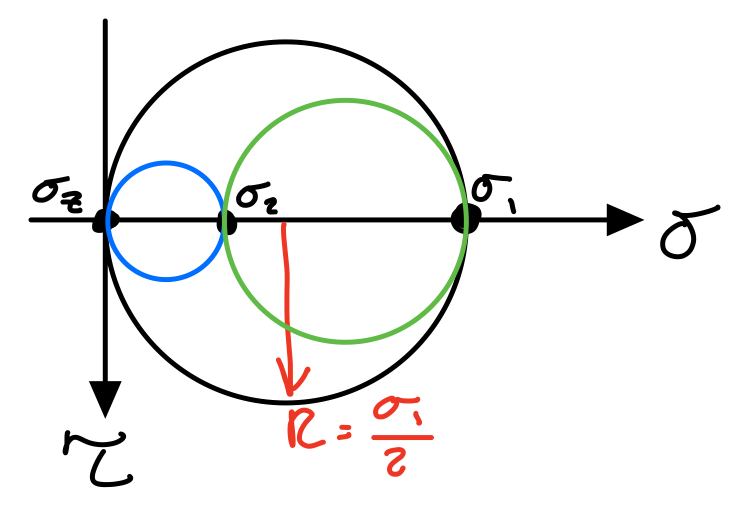
Tresca with same signs.

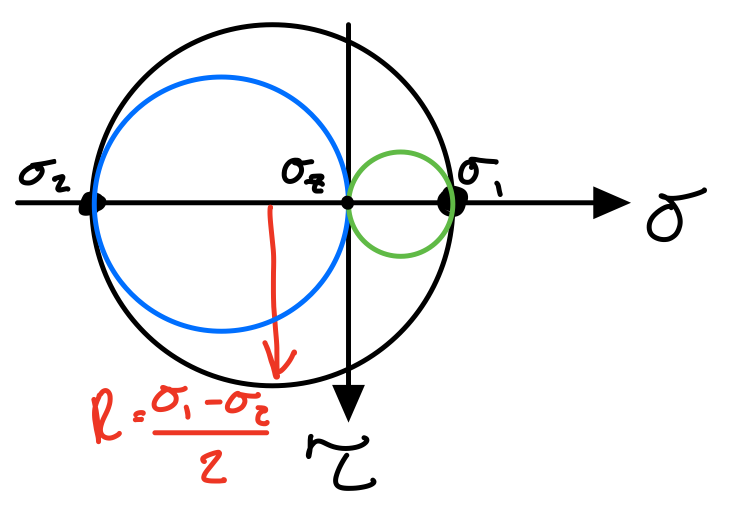
$$ \begin{align} |\sigma_1| = \sigma_Y \\ |\sigma_2| = \sigma_Y \end{align} $$

If $ \sigma_1 $ and $ \sigma_2 $ have opposite signs:

Tresca with opposite signs.

$$ |\sigma_1 - \sigma_2| = \sigma_Y\ $$

Maximum Distortion Energy (Von Mises) Criterion

Ductile materials likely do not fail due to stresses that only result in a volume change. It is hypothesized that failure is driven by distortion strain energy.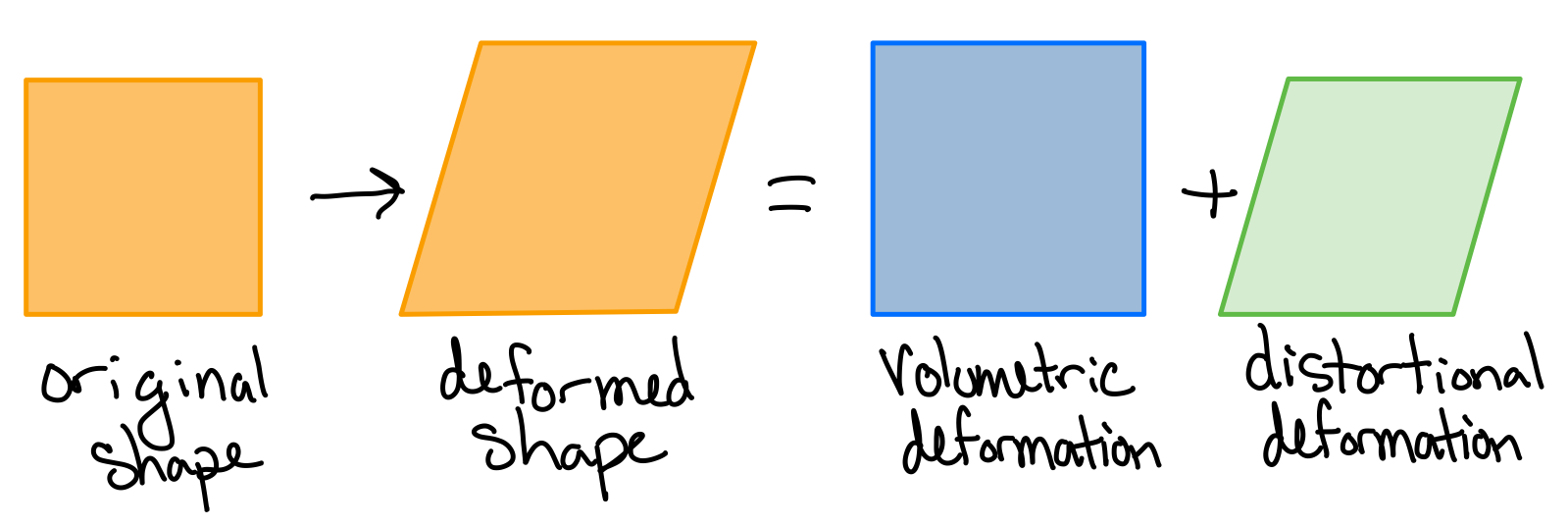

All elastic deformations can be broken down into volumetric and distortional deformations. The total strain energy $ W $ in a material is broken into these same parts.

$$ W = W_v + W_d\ $$

Von Mises material failure. #von-mis

$$ \sigma_{VM} = \sqrt{\sigma_1^2 - \sigma_1 \sigma_2 + \sigma_2^2} \ge \sigma_Y\ $$

Strain energy density for plane stress.

$$ W_d = \frac{1+\nu}{3E}(\sigma_1^2 - \sigma_1 \sigma_2 + \sigma_2^2)\ $$

Strain energy density at the moment of yield.

$$ W_{d,yield} = \frac{1+\nu}{3E}\sigma_Y^2\ $$

Equating the plane stress and moment of yield equations.

$$ \sigma_1^2 - \sigma_1 \sigma_2 + \sigma_2^2 = \sigma_Y^2\ $$

Von Mises at yield.

$$ \sigma_{VM}^2 = \sigma_Y^2\ $$

The equating equation be plotted to show the failure surface. The elliptical surface is the Von Mises surface overlaid with the Teresca surface. Loading conditions that occur outside of the surface are when the material fails.

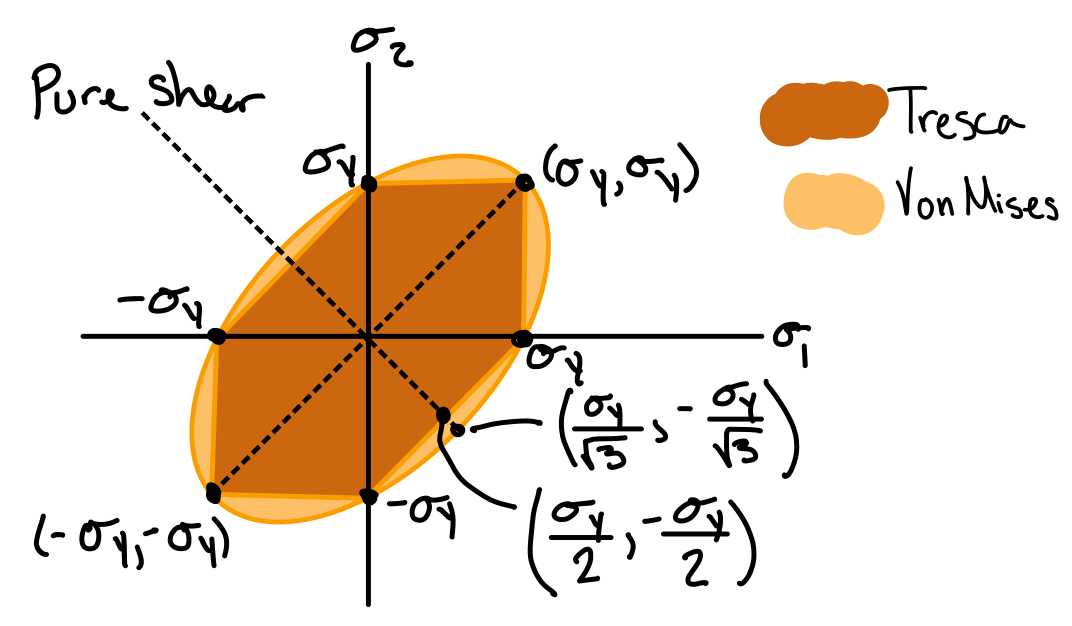
Interactive 3D Failure Surfaces

The following figure shows the failure surfaces of Tresca and von Mises criteria in term of the principal stresses in 3 dimensions. The 2D figure above can be found cenered around the origin in this plot. The shape of the 2D failure surface $ (\sigma_1,\sigma_2) $ remains the same, but moves location depending on $ \sigma_3 $. Just like in 2D, regions outside the surfaces are considered to have failed.

Note: Click and drag to rotate, scroll to zoom, and click legend entries to toggle.

Maximum Normal Stress Criterion

For brittle materials, failure is caused by the maximum tensile stress and NOT compressive stress.

Maximum normal stress criterion material failure.

$$ \begin{align} |\sigma_1| = \sigma_{ult} \\ |\sigma_2| = \sigma_{ult} \end{align} $$

The $ \sigma_1 $ and $ \sigma_2 $ equations can be plotted to show the failure surface. Loading conditions that occur outside of the surface are when the material fails. Brittle fracture can be difficult to predict, so use this theory with caution