Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Buckling

    Buckling is the sudden change in shape of a structural component under a compressive load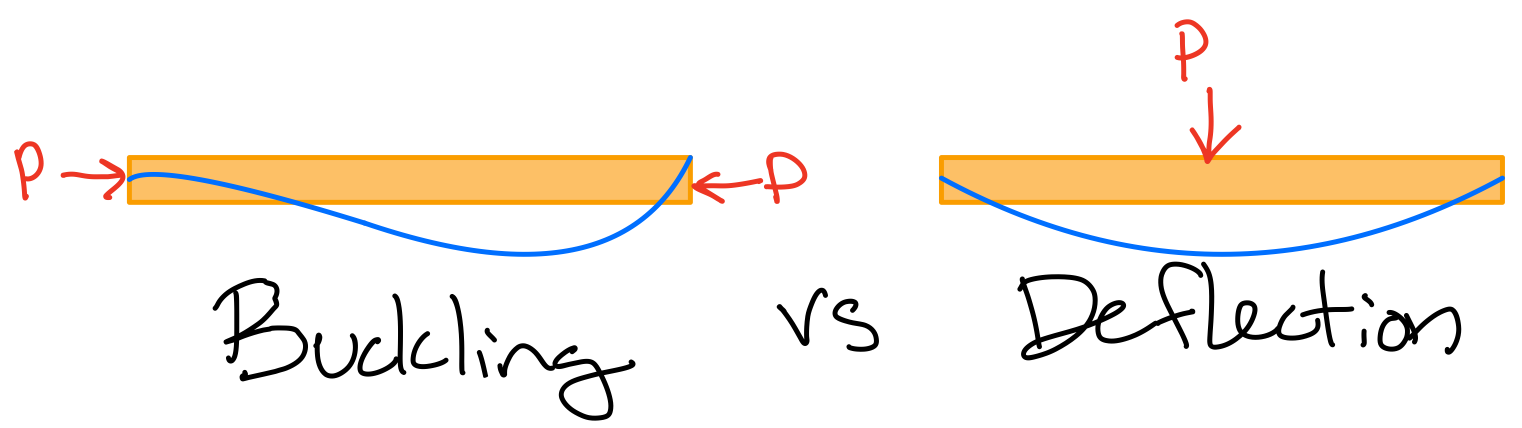
    The beam is still able to withstand normal loads, but buckling causes an instability. Small perturbations make the structure unstable. Failure is elastic (\( \sigma < \sigma_Y \)), but if increased loads are applied, further deformation and plastic failure (yielding) / brittle failure (fracture) can occur (post-buckling failure).

    Stability of Structures

    Single Column

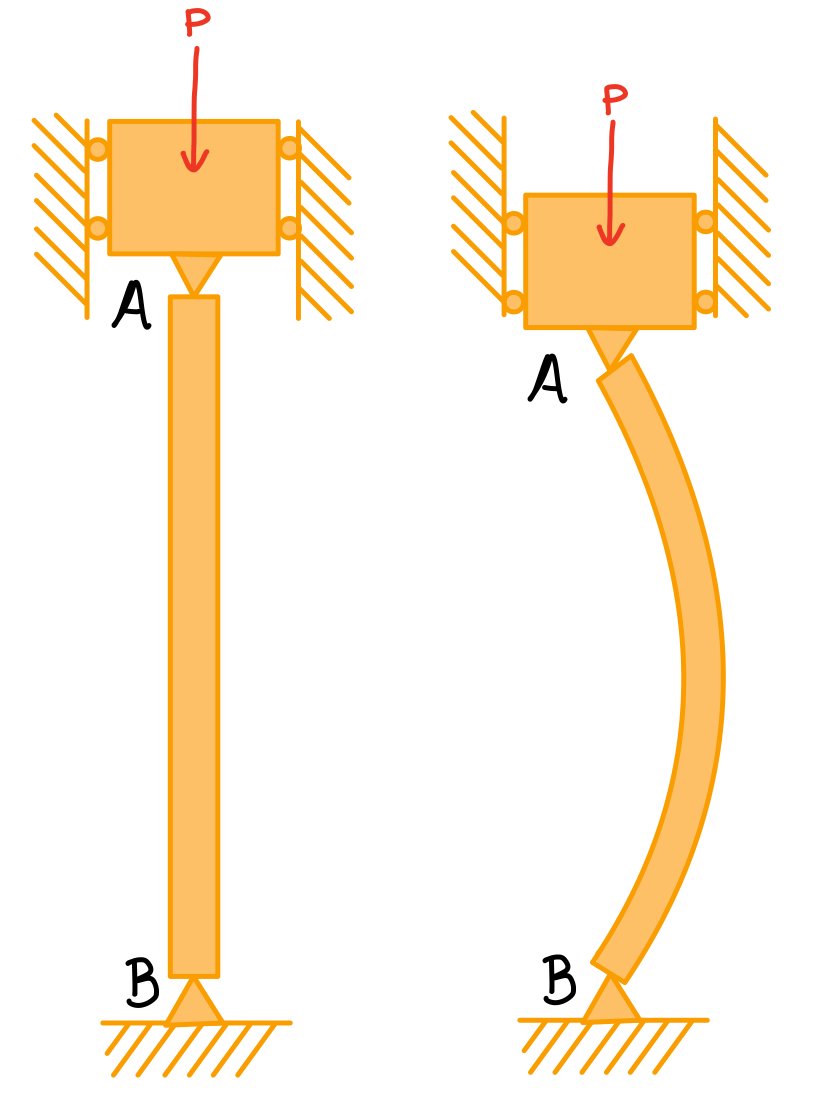
    Column \( AB \) is supporting uniaxial compressive load \( P \). To properly design this column, the cross-section must satisfy two equations.
    Uniaxial compressive load on single column.
    $$ \begin{align} \sigma = \frac{P}{A} \le \sigma_{all} \\ \delta = \frac{PL}{EA} \le \delta_{spec} \end{align} $$
    Increasing the load can cause the column to buckle \( \rightarrow \) instability causing failure.

    Two Rods and a Torsional Spring

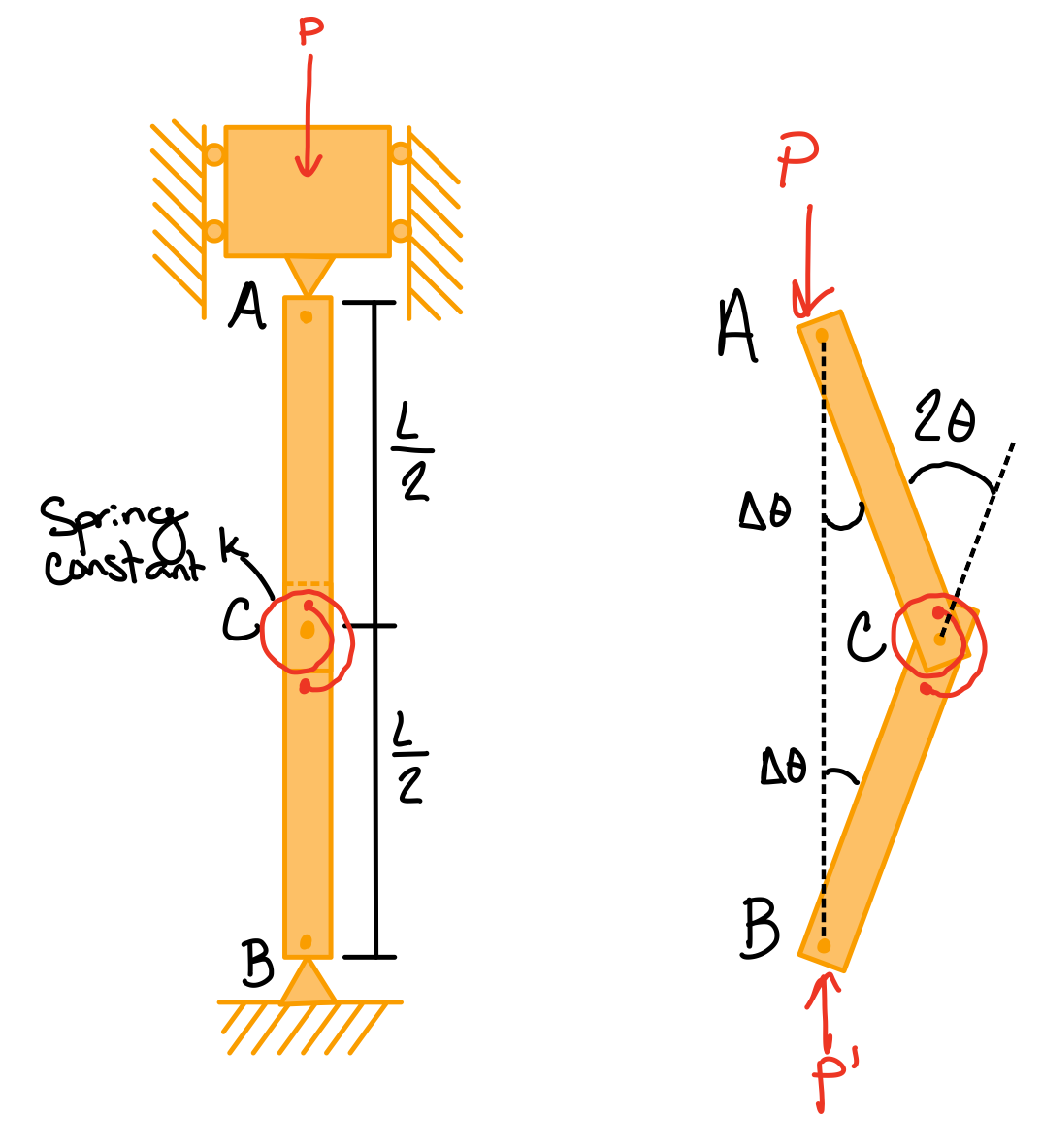
    Rods \( AC \) and \( CB \) are perfectly aligned and a torsional spring connects them at point \( C \). For small perturbations, point \( C \) moves to the right.
    • If \( C \) returns to the original position, then the system is stable
    • If \( C \) moves farther away from the original position, then the system is unstable
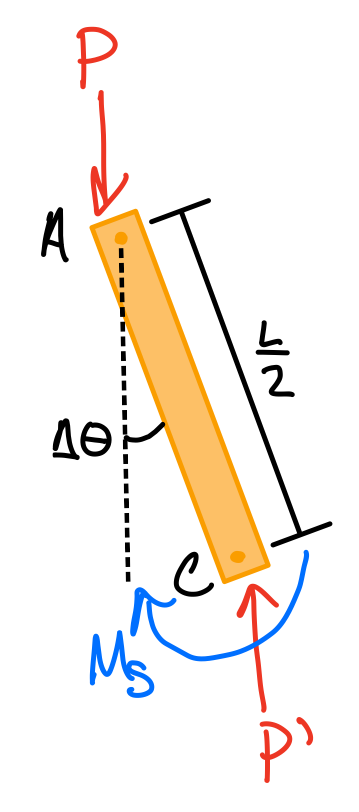
    Spring restoring moment.
    $$ M_s = K(2\Delta\theta)= \text{restoring moment}\ $$
    The resultant moment from the applied load \( P \) tends to move the rod away from the vertical position.
    Sprind destabilizing moment.
    $$ M_{load} = P\frac{L}{2}\sin\Delta\theta = P\frac{L}{2}\Delta\theta = \text{destabilizing moment}\ $$
    • Stable system: \( M > M_{load} \)
    • Unstable system: \( M< M_{load} \)
    • Equilibrium position gives:\( M=M_{load} \)
    Critical load. #crt-lod
    $$ P_{cr} = \frac{4K}{L}\ $$
    $$ M_s = M_{load} $$
    $$ K(2\Delta\theta) = P_{cr}\frac{L}{2}\Delta\theta $$

    Euler's Formula

    Euler's formula can be used to solve for the critical load of a uniaxially loaded column.

    Pinned-end Columns

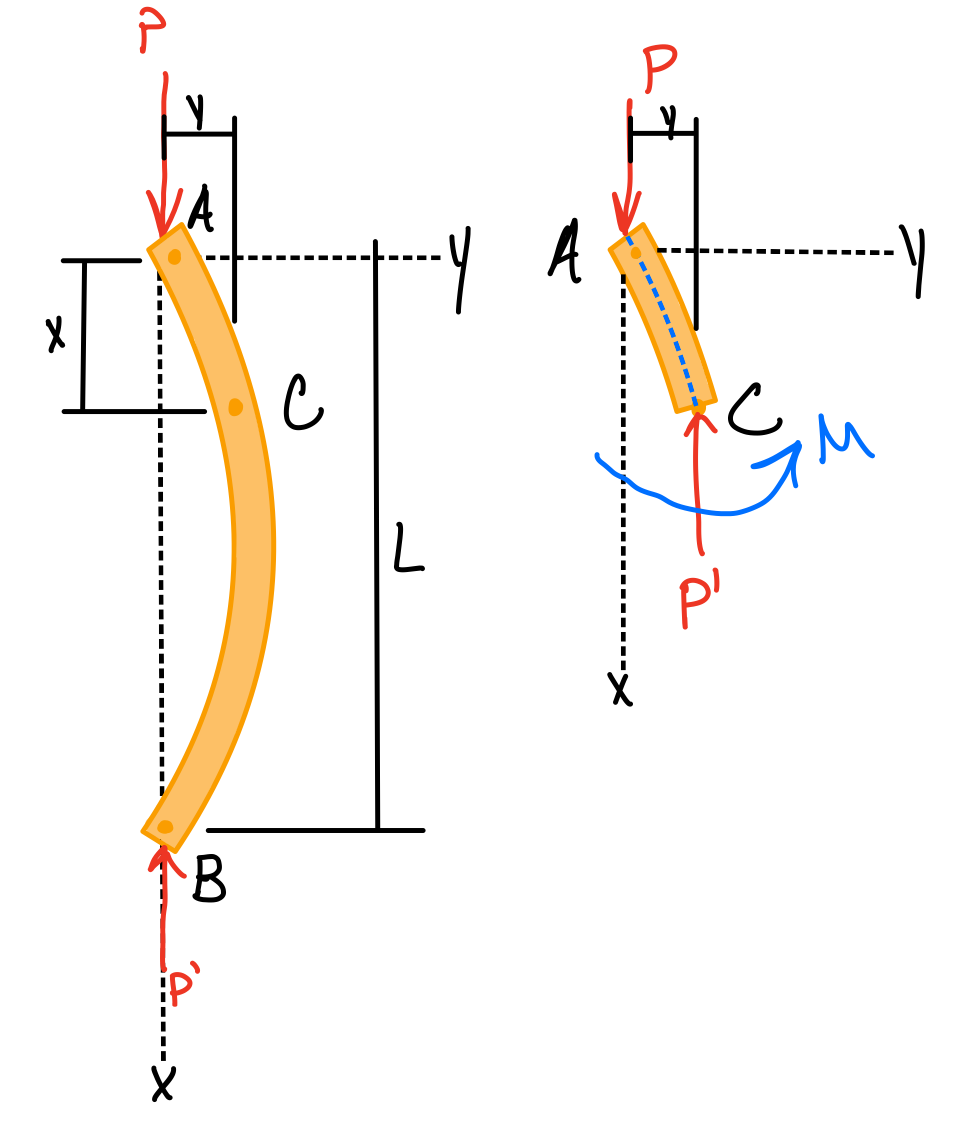
    Rod \( AB \) is pinned on each end. After a small perturbation, the system reaches equilibrium.
    Pinned-end equilibrium. #pin-end
    $$ y''(x) + \frac{P}{EI}y(x) = 0\ $$
    $$ M(x) = EIy''(x)\ $$
    $$ M = -Py(x)\ $$
    $$ EIy''(x) = -Py(x)\ $$
    Linear, homogeneous differential equation of second order with constant coefficients.
    General solution.
    $$ y(x) = A\sin(px) + B\cos(px)\ $$
    Boundary conditions.
    $$ y(0) = y(L) = 0\ $$
    Euler's formula for buckling. #axl-fdr
    $$ \begin{align} P_{cr} = \frac{\pi^2EI}{L^2} \\ \text{where } P > P_{cr} \end{align} $$
    $$ y(x) = A\sin(\sqrt{\frac{P}{EI}}x) + B\cos(\sqrt{\frac{P}{EI}}x)\ $$
    $$ y(x=0)=0 \rightarrow A\sin(0)+B\cos(0) = 0\ $$
    $$ B=0\ $$
    $$ y(x=L)=0 \rightarrow A\sin(\sqrt{\frac{P}{EI}}L)+0 = 0\ $$
    $$ A\sin(\sqrt{\frac{P}{EI}}L)=0\ $$
    This has two solutions
    $$ A = 0 \rightarrow \text{not interesting}\ $$
    $$ A = n \rightarrow n \text{ (any number) except where } A\sin(\sqrt{\frac{P}{EI}}L) = n\pi $$
    $$ \frac{P}{EI}L^2 = n^2\pi^2\ $$
    $$ P_{cr} = \frac{n^2\pi^2EI}{L^2}\ $$
    Buckling usually happens at the smallest non-zero value of \( P_{cr} \).
    $$ n=1\ $$
    Higher \( n \) values can be achieved if columns are prevented from buckling at \( n=1 \).

    Other Boundary Conditions

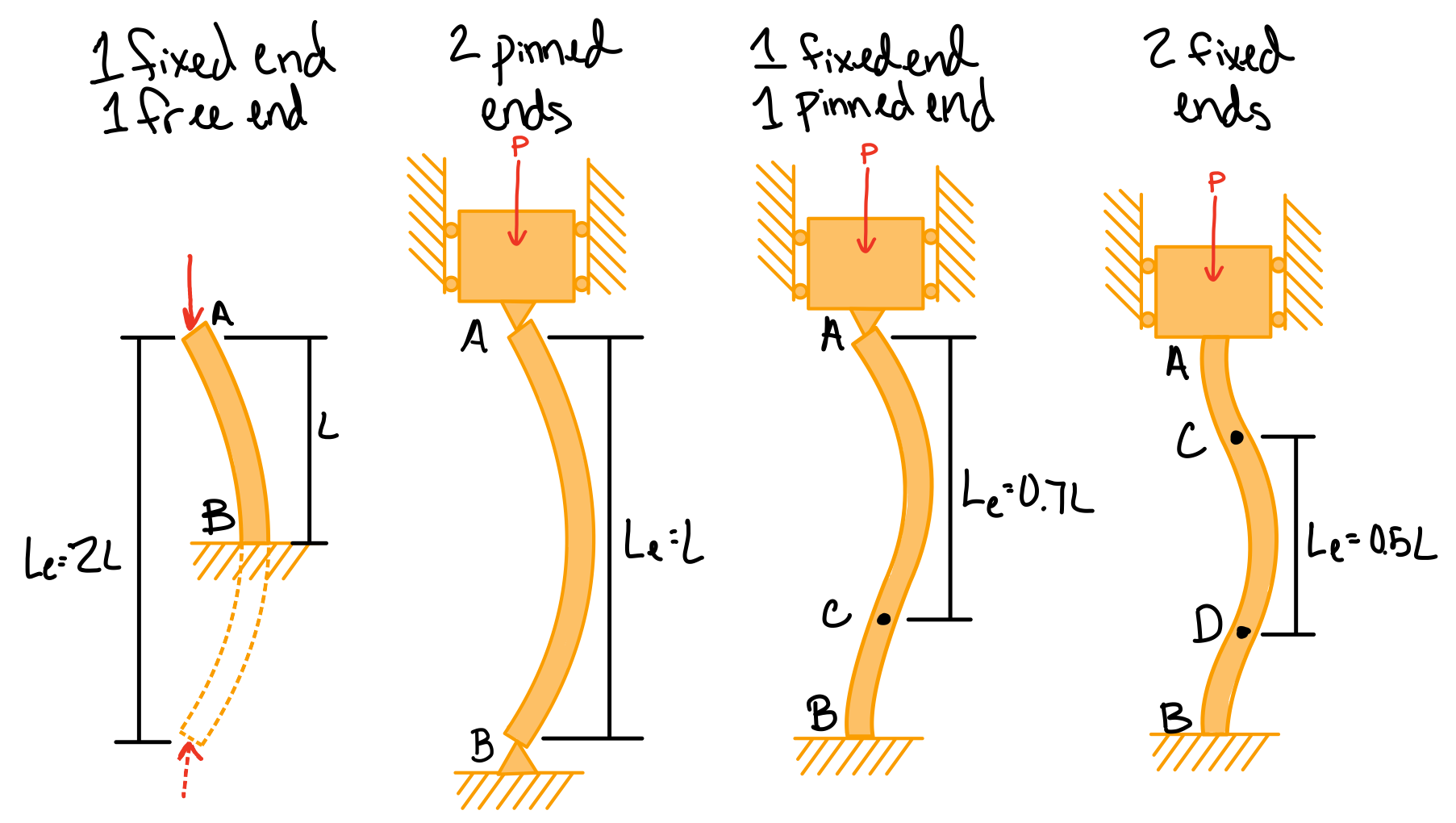
    Different boundary conditions change the length used in the critical load formula resulting in an effective length (\( L_e \)).
    General critical load formula.
    $$ P_{cr} = \frac{\pi^2EI}{L_e^2}\ $$