Beam Deflection

Goal: Determine the deflection and slope at specified points of beams and shafts.
Solve statically indeterminate beams: where the number of reactions at the supports exceeds the number of equilibrium equations available.
Maximum deflection of the beam: Design specifications of a beam will generally include a maximum allowable value for its deflection.

Sign Conventions

Boundary Conditions

Moment-Curvature Equation

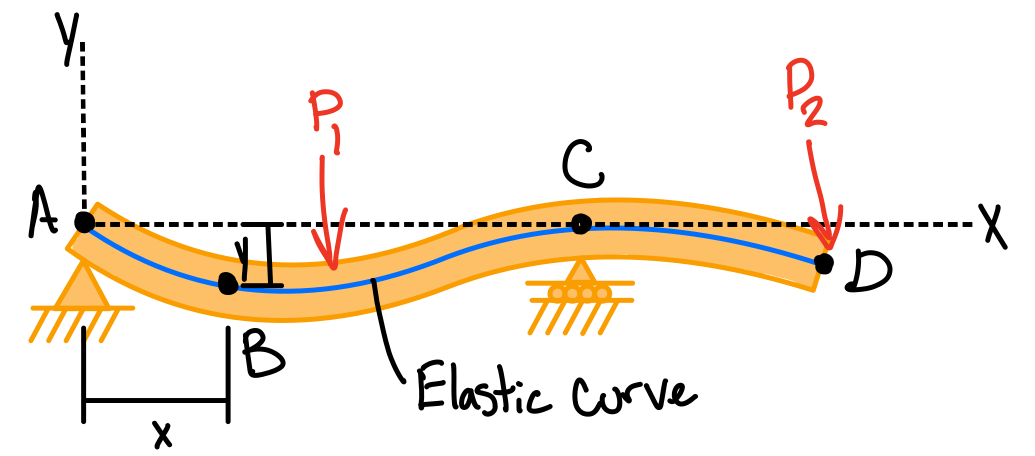
The physical shape of the deflected beam is called the elastic curve. The curvature $ \kappa $ can be found by rearranging the bending moment $ M(x) $ equation, and for small angles, can be approximated by the second derivative of $ y(x) $.

Moment-curve equation. #els-crv

$$ \kappa = \frac{1}{\rho} \approx y''(x) $$

$$ M(x) = \frac{E(x)I(x)}{\rho(x)} $$

$$ \frac{1}{\rho} = \frac{M(x)}{EI} $$

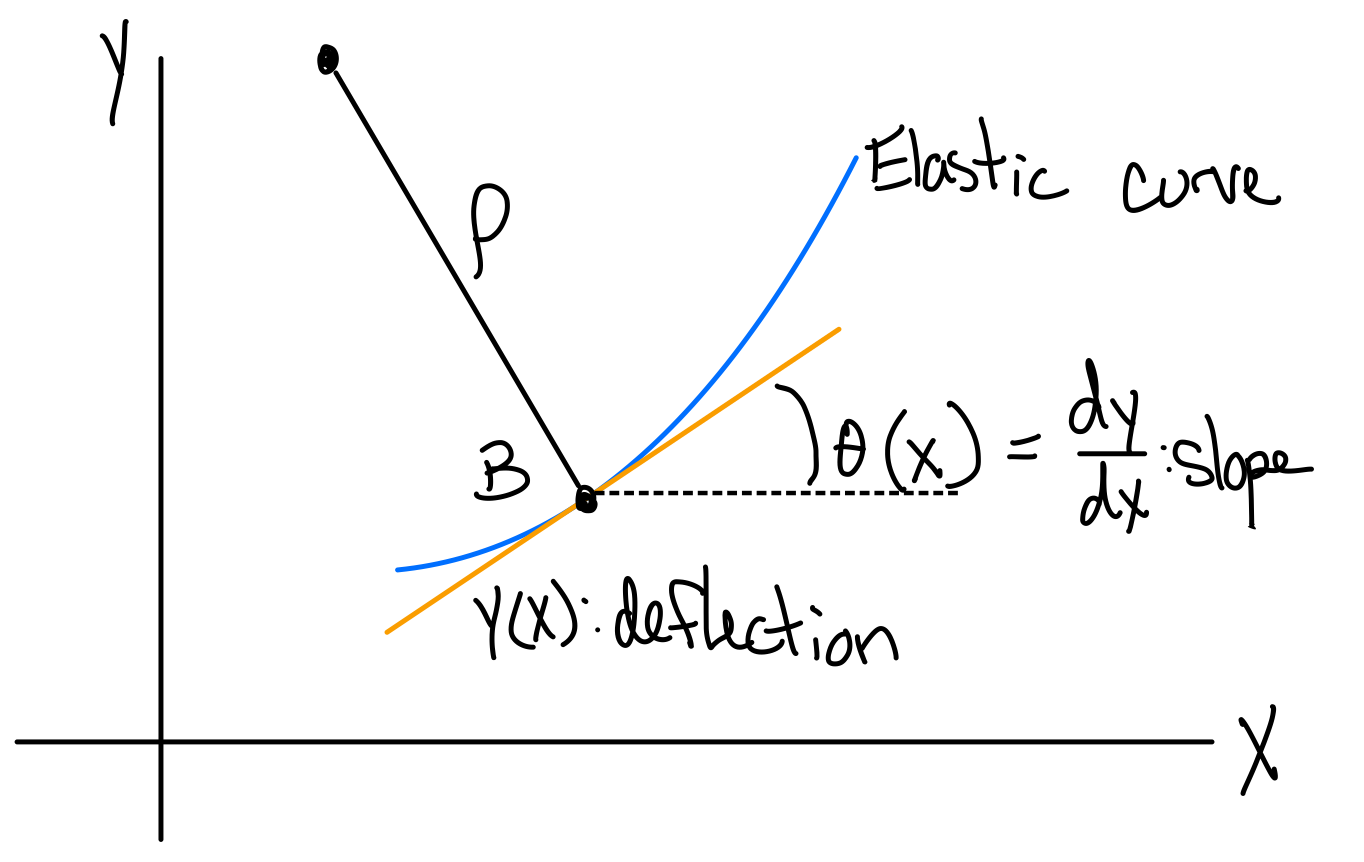
Elastic curve governing equation.

$$ \frac{d^2y}{dx^2} = \frac{M(x)}{EI}\ $$

To find the deflection shape:

Find the bending moment $ M(x) $.
Integrate both sides of the governing equation twice.
Solve for $ y(x) $.

Assumptions

$ y(x) $ is the vertical direction
Bending only: we will neglect effects of transverse shear
Small deflection angles

Differentiation

Elastic curve equation for constant E and I.

$$ EIy''(x) = M(x) $$

Differentiating the elastic curve equation.

$$ EIy'''(x) = \frac{dM(x)}{dx} = V(x) $$

Differentiating the elastic curve equation a second time.

$$ EIy''''(x) = \frac{dV(x)}{dx} = w(x) $$

$ EIy''(x): $ bending moment
$ EIy '''(x): $ shear force
$ EIy''''(x): $ distributed load

Integration

Shear force.

$$ V(x) = \int w(x) dx\ $$

Internal bending moment.

$$ M(x) = \int V(x)dx\ $$

Slope of the tangent line.

$$ \frac{dy}{dx} = \int \frac{1}{EI}M(x)dx\ $$

Deflection.

$$ y(x) = \int y'(x) dx\ $$

$ y(x): $ deflection
$ y'(x): $ slope

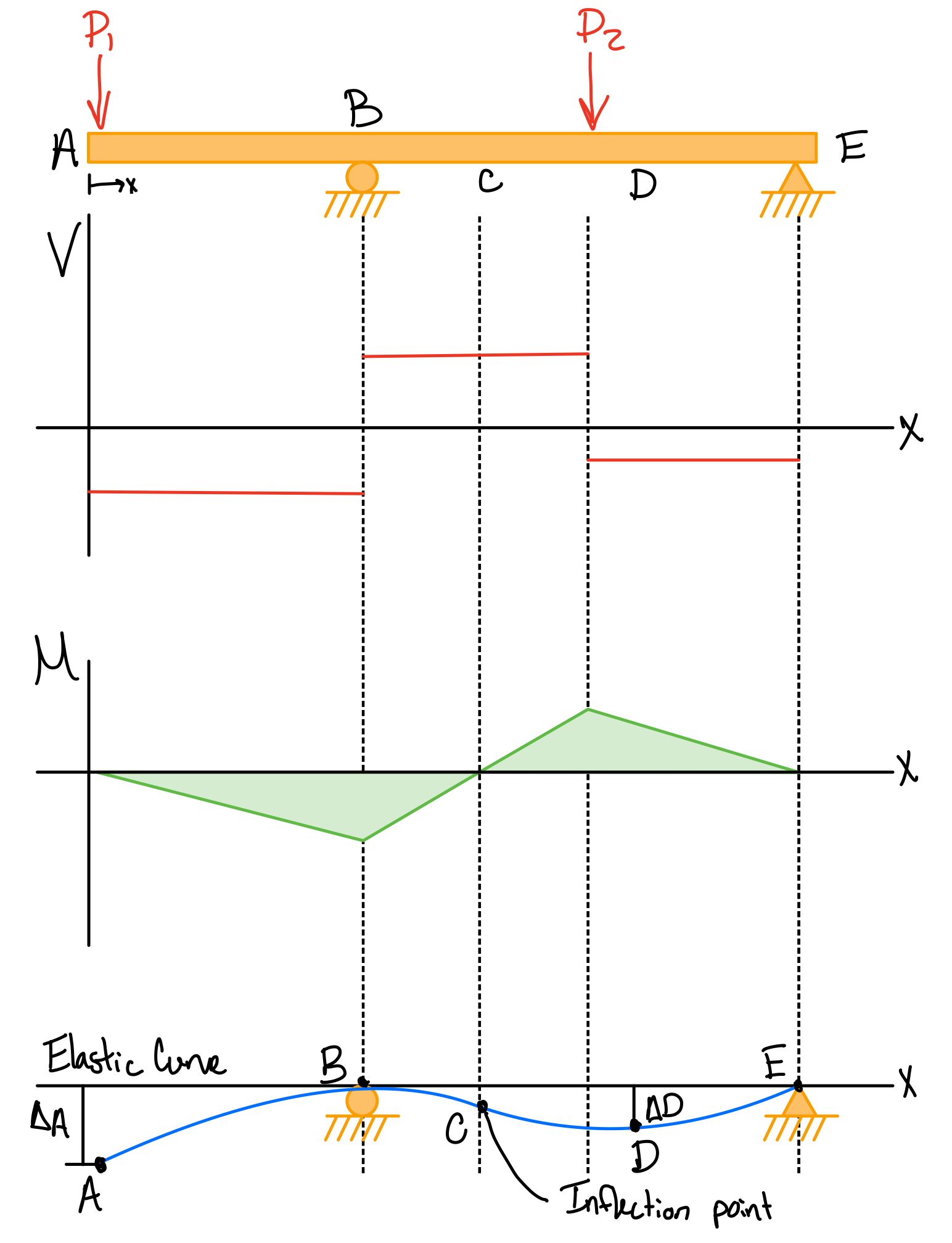
Example: Overhanging beam. #ovr-hng

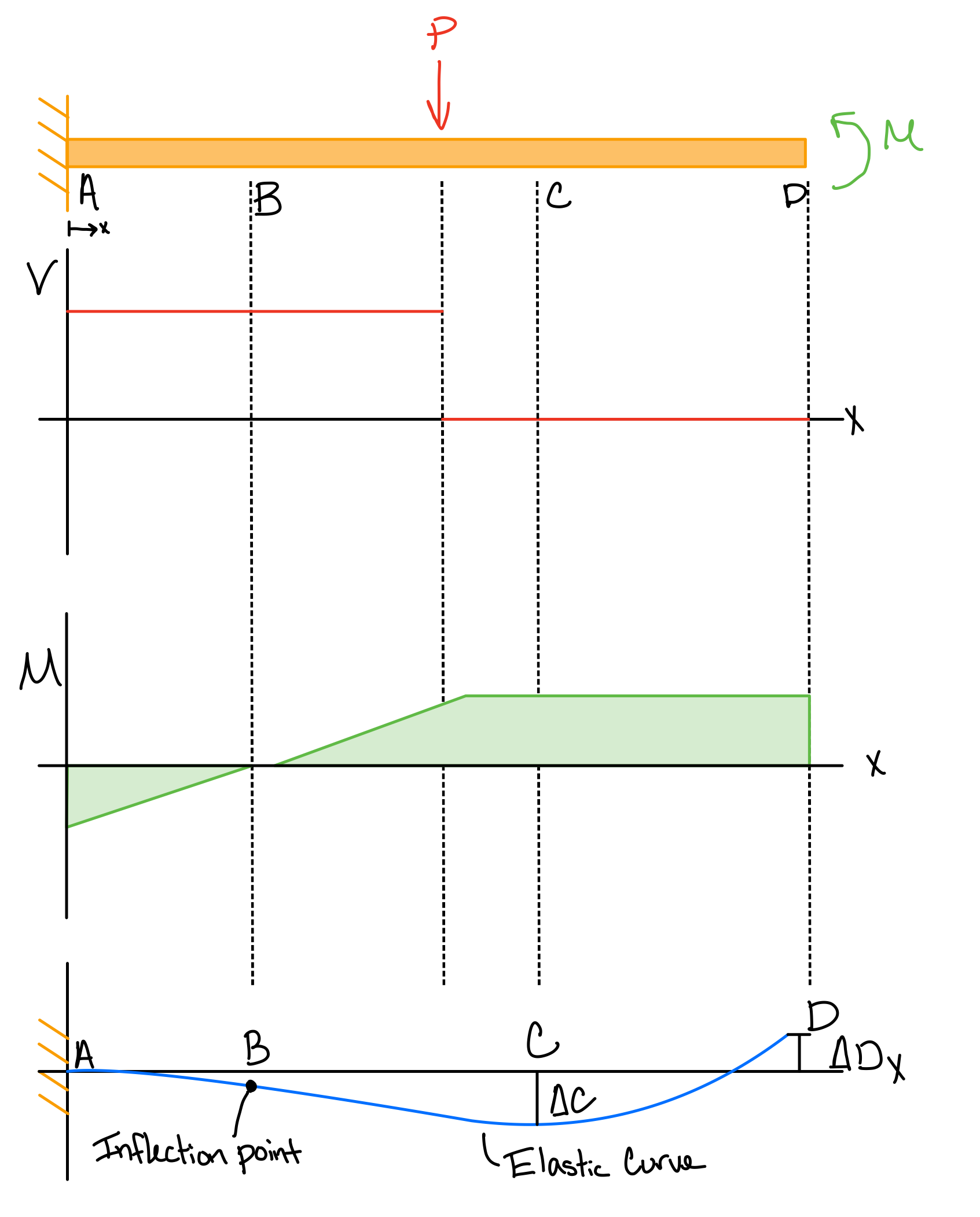
Example: Cantilever beam. #can-tlv

Beam Solutions

Common beam deflection solutions have been worked out.

Max. deflection $ y_{max} $	Slope at end $ \theta $	Elastic curve $ y(x) $
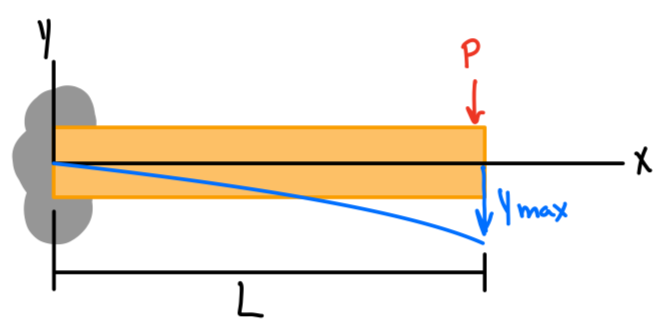$ -\frac{PL^3}{3EI} $	$ -\frac{PL^2}{2EI} $	$ \frac{P}{6EI}(x^3-3Lx^2) $
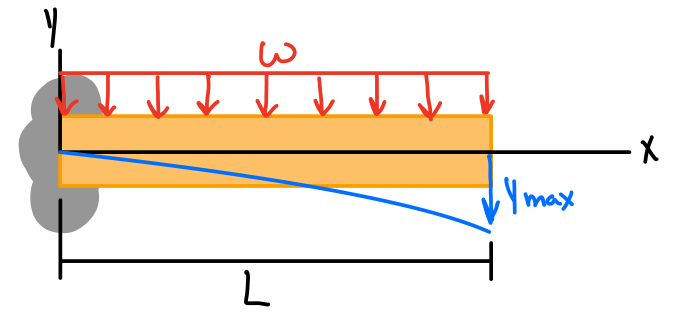$ -\frac{wL^4}{8EI} $	$ -\frac{wL^3}{6EI} $	$ -\frac{w}{24EI}(x^4-4Lx^3+6L^2x^2) $
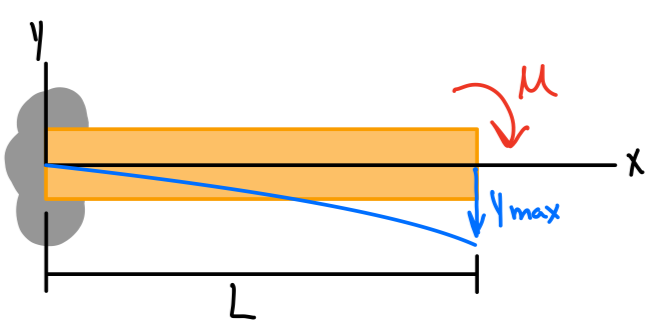$ -\frac{ML^2}{2EI} $	$ -\frac{ML}{EI} $	$ -\frac{M}{2EI}x^2 $
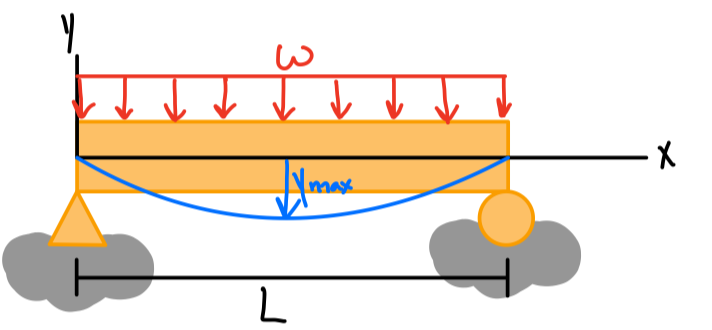$ -\frac{5wL^4}{384EI} $	$ \pm\frac{wL^3}{24EI} $	$ -\frac{w}{24EI}(x^4-2Lx^3+L^3x) $
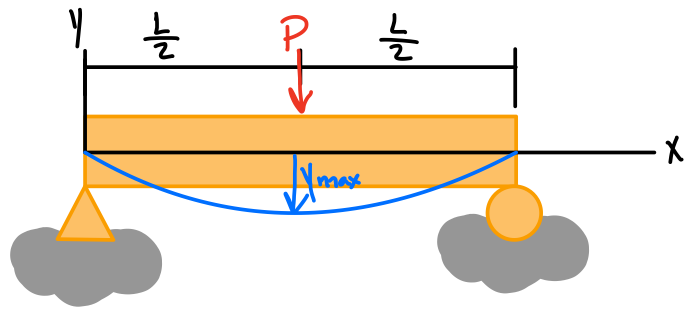$ -\frac{PL^3}{48EI} $	$ \pm\frac{PL^2}{16EI} $	For $ 0 \le x \le \frac{L}{2}: $ $ \frac{P}{48EI}(4x^3-3L^2x) $
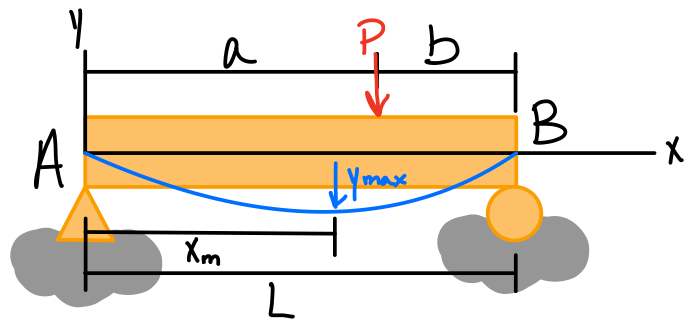For $ a>b: $ $ -\frac{Pb(L^2-b^2)^{\frac{3}{2}}}{9\sqrt{3}EIL} $ $ x_m = \sqrt{\frac{L^2-b^2}{3}} $	$ B: -\frac{Pb(L^2-b^2)}{6EIL} $ $ A: +\frac{Pa(L^2-a^2)}{6EIL} $	For $ x<a: $ $ \frac{Pb}{6EIL}(x^3-x(L^2-b^2)) $ For $ x=a: $ $ -\frac{Pa^2 b^2}{3EIL} $
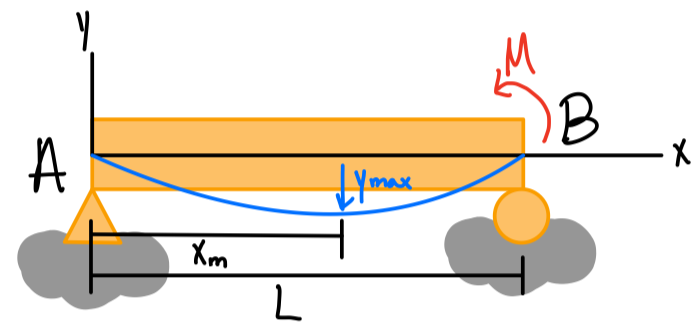$ -\frac{ML^2}{9\sqrt{3}EI} $ $ x_m = \frac{L}{\sqrt{3}} $	$ A: -\frac{ML}{6EI} $ $ B: +\frac{ML}{3EI} $	$ \frac{M}{6EIL}(x^3-L^2x) $

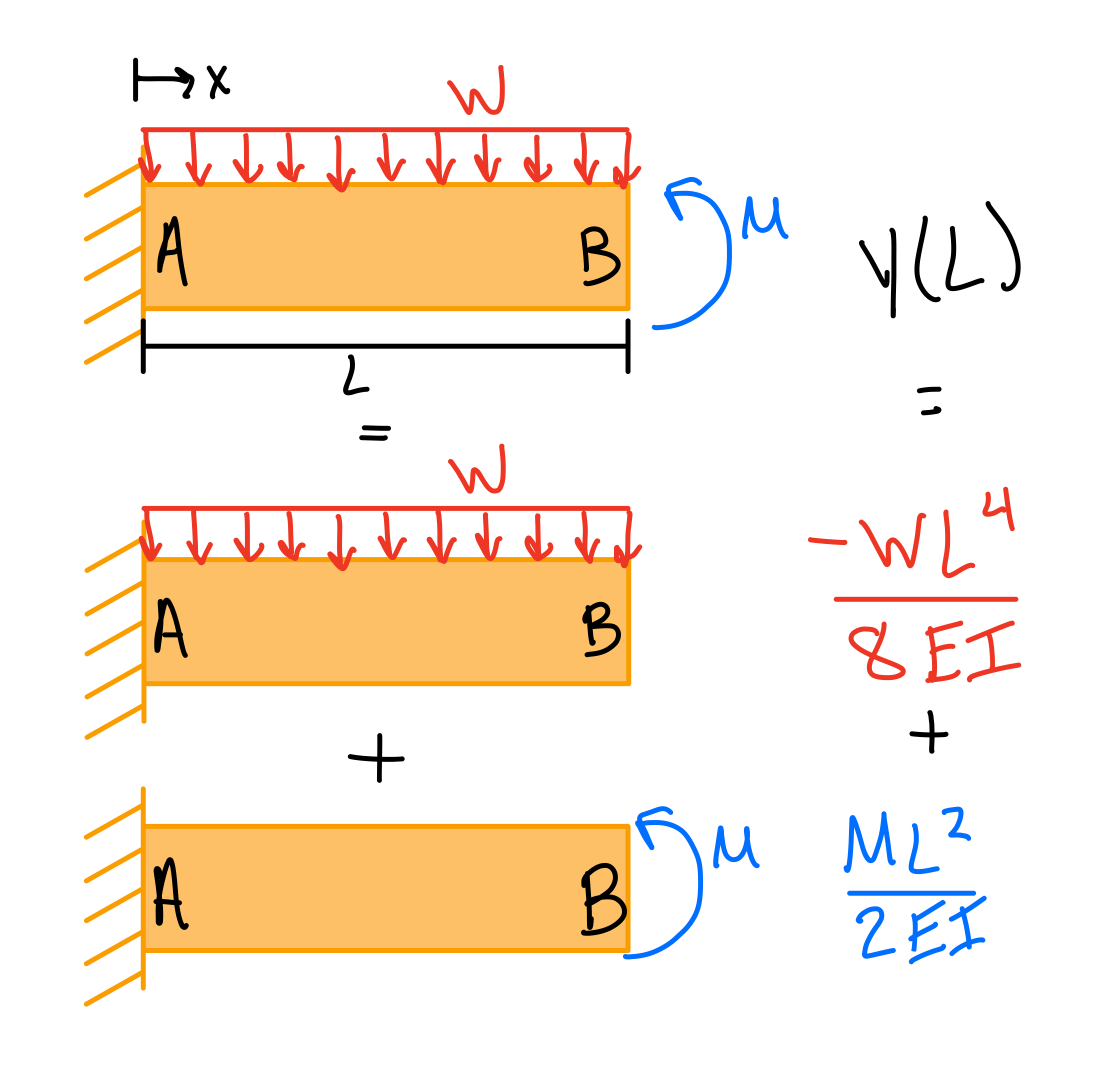
To solve loadings that are not in the table, use superposition to get the resulting deflection curve.

Example: Deflection from a moment and distributed load using superpositon. #dfl-spp

Max. deflection \( y_{max} \)	Slope at end \( \theta \)	Elastic curve \( y(x) \)
\( -\frac{PL^3}{3EI} \)	\( -\frac{PL^2}{2EI} \)	\( \frac{P}{6EI}(x^3-3Lx^2) \)
\( -\frac{wL^4}{8EI} \)	\( -\frac{wL^3}{6EI} \)	\( -\frac{w}{24EI}(x^4-4Lx^3+6L^2x^2) \)
\( -\frac{ML^2}{2EI} \)	\( -\frac{ML}{EI} \)	\( -\frac{M}{2EI}x^2 \)
\( -\frac{5wL^4}{384EI} \)	\( \pm\frac{wL^3}{24EI} \)	\( -\frac{w}{24EI}(x^4-2Lx^3+L^3x) \)
\( -\frac{PL^3}{48EI} \)	\( \pm\frac{PL^2}{16EI} \)	For \( 0 \le x \le \frac{L}{2}: \) \( \frac{P}{48EI}(4x^3-3L^2x) \)
For \( a>b: \) \( -\frac{Pb(L^2-b^2)^{\frac{3}{2}}}{9\sqrt{3}EIL} \) \( x_m = \sqrt{\frac{L^2-b^2}{3}} \)	\( B: -\frac{Pb(L^2-b^2)}{6EIL} \) \( A: +\frac{Pa(L^2-a^2)}{6EIL} \)	For \( x<a: \) \( \frac{Pb}{6EIL}(x^3-x(L^2-b^2)) \) For \( x=a: \) \( -\frac{Pa^2 b^2}{3EIL} \)
\( -\frac{ML^2}{9\sqrt{3}EI} \) \( x_m = \frac{L}{\sqrt{3}} \)	\( A: -\frac{ML}{6EI} \) \( B: +\frac{ML}{3EI} \)	\( \frac{M}{6EIL}(x^3-L^2x) \)