Mechanical Science & Engineering
MechSE Reference Pages

    Scroll back to top

    Axial Loading

    Notation and Convention

    Notation
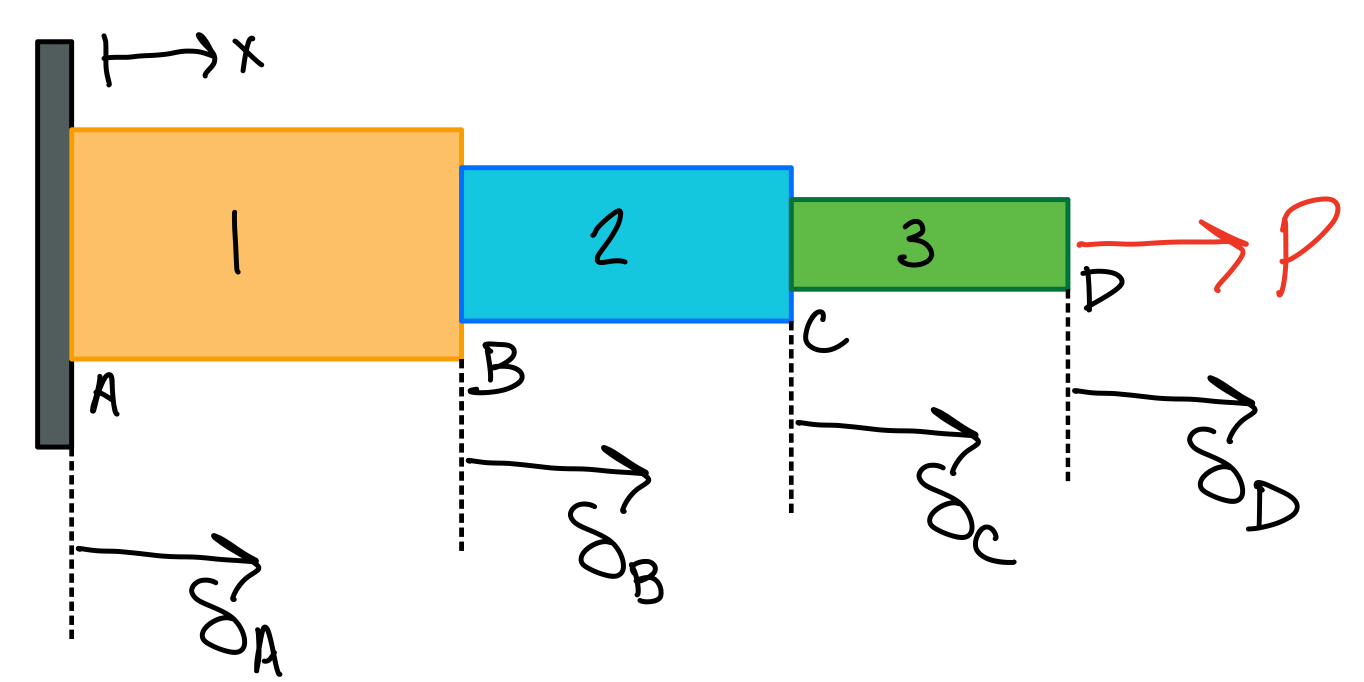
    • Displacement of points in space: the movement of a point relative to its initial position in space (ex; \( \delta_B \) )
    • Change in length of a segment: the relative displacement of a point with respect to another point (ex; \( \delta_{B/A} = \delta_B - \delta_A = \delta_1 \) ). This can be written multiple ways:
      Notation.
      $$ \delta_{AD} \equiv \delta_{DA} \equiv \delta_{A/D} \equiv \delta_{D/A}\ $$
    Sign Conventions for internal forces in a bar.
    • \( F>0 \) : tension
    • \( F<0 \) : compression
    • \( \delta>0 \) : elongation
    • \( \delta<0 \) : contraction

    Saint-Venant's Principle: slender beam case

    Notation

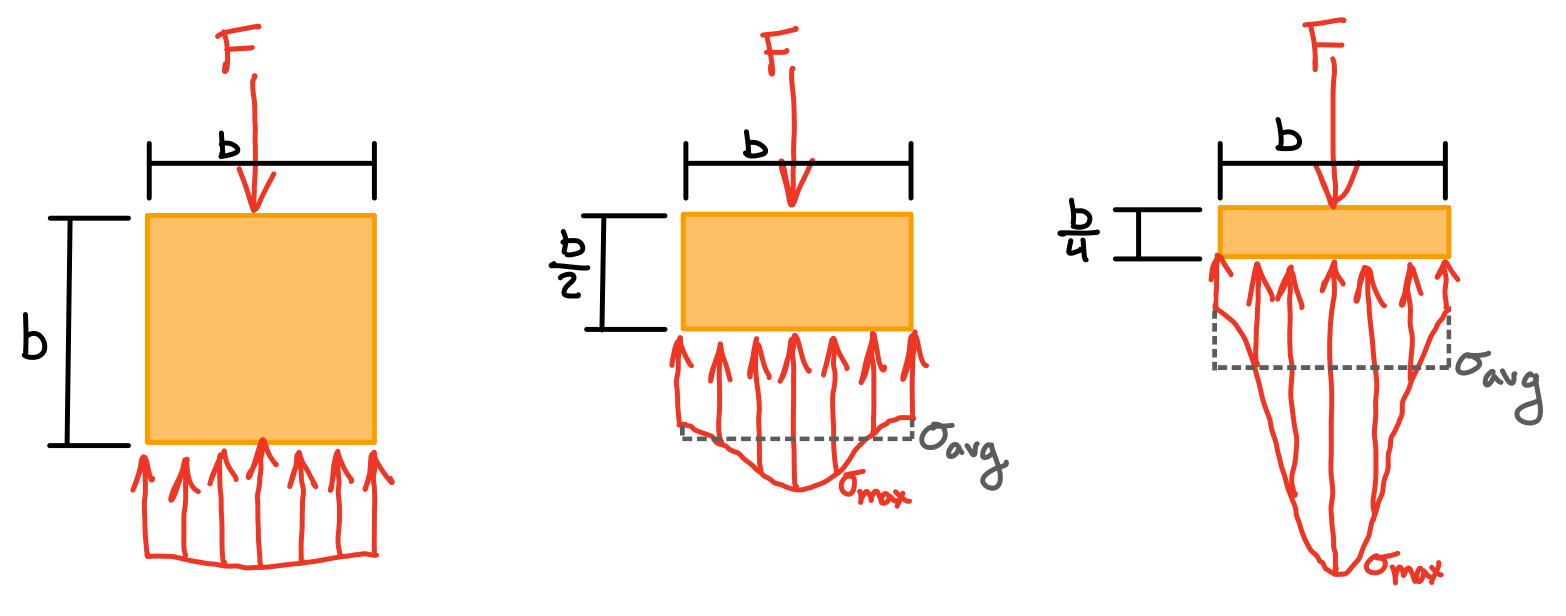
    Stress analysis very near to the point of application of load \( P \). Saint-Venant's principle: the stress and strain produced at points in a body sufficiently removed* from the region of external load application will be the same as the stress and strain produced by any other applied external loading that has the same statically equivalent resultant and is applied to the body within the same region.

    *farther than the widest dimension of the cross section

    Force-Deformation Relation

    Relation. #axl-fdr
    $$ \delta = \frac{PL}{EA}\ $$
    $$ P = \sigma A\ $$
    $$ P = E \varepsilon A\ $$
    $$ P = E\frac{\delta}{L}A\ $$
    Axial flexibility.
    $$ \delta = fP => f = \frac{L}{EA}\ $$
    Axial stiffness.
    $$ P = k\delta => k = \frac{EA}{L}\ $$

    Axially Varying Properties

    For non-uniform load, material property and cross-section area:
    Variable properties. #sts-vpr
    $$ \delta = \int_0^L\frac{F(x)}{E(x)A(x)}dx\ $$
    $$ \sigma = E\varepsilon\ $$
    $$ \frac{F(x)}{A(x)} = E(x)\varepsilon(x)\ $$
    $$ \frac{F(x)}{A(x)} = E(x)\frac{d\delta(x)}{dx}\ $$
    $$ d\delta = \frac{F(x)}{E(x)A(x)}dx\ $$
    Assume variations with \( x \) are "mild" (on length scale longer than cross-sectional length scales)

    Principle of Superposition

    Superposition: If the displacements are (1) small and (2) linearly related to the force components acting, the displacements caused by the components can be added up:
    Superposition.
    $$ \delta = \sum_i \delta_i = \sum_i \frac{F_i L_i}{E_i A_i}\ $$

    General Solving Procedure

    1. Draw a FBD
    2. Equilibrium equations: force balance and moment balance
    3. Constitutive equations: stress-strain or force-displacement relations
    4. Compatibility equations: geometric constraints

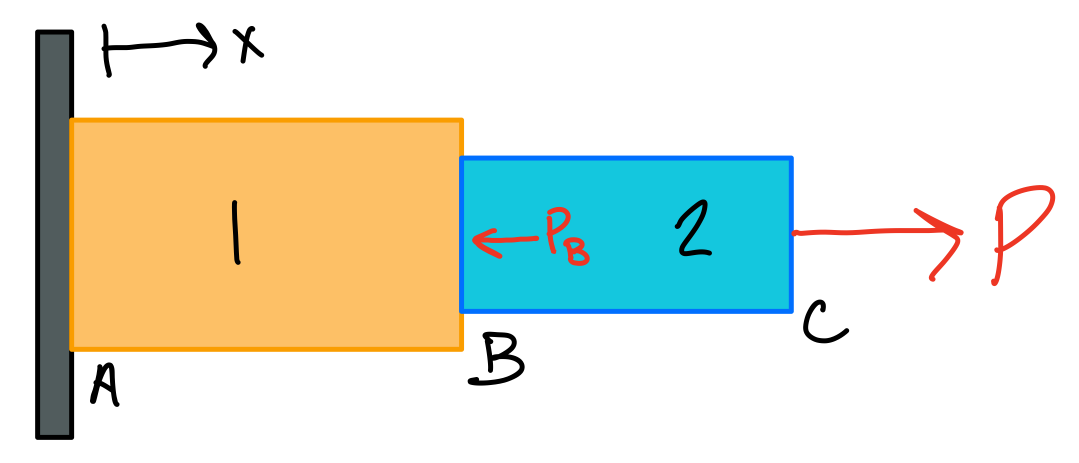
    Statically Determinate Problems

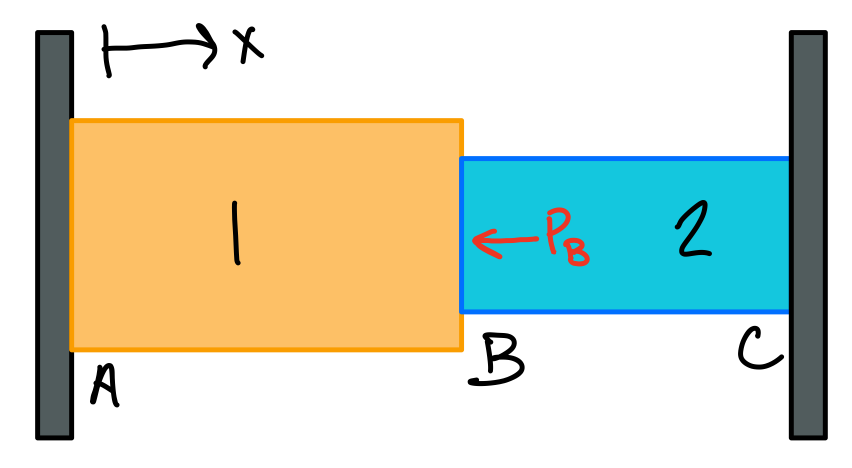
    Statically determinate
    All internal forces can be obtained from equilibrium analysis only

    Statically Indeterminate Problems

    Statically indeterminate
    Equilibrium does not determine all internal forces.

    Thermal Effects: Temperature Changes

    Notation
    • \( \Delta T > 0, \sigma < 0 \) : Compression
    • \( \Delta T < 0, \sigma > 0 \) : Tension

    \( \delta_T \) , \( \varepsilon_T \) present in addition to elastic \( \delta_E \) , \( \varepsilon_E \) (from internal forces). Superposition (small strains):

    Total strain.
    $$ \varepsilon_{tot} = \varepsilon_{E} + \varepsilon_{T}\ $$
    Total displacement.
    $$ \delta_{tot} = \delta_{E} + \delta_{T}\ $$

    Temperature changes with no applied loads
    A rod rests freely on a smooth horizontal surface. Temperature of the rod is raised by \( \Delta T \). Rod elongates by an amount.
    Displacement from temperature changes.
    $$ \delta_{T} = \alpha \Delta T L\ $$
    Linear coefficient of thermal expansion \( \alpha \), \( [\alpha] = \frac{1}{K},\frac{1}{°C},... \). This deformation is associated with an average thermal strain:
    Strain from temperature changes.
    $$ \varepsilon_{T} = \frac{\delta_T}{L} = \alpha T\ $$
    Temperature changes with statically indeterminate beam
    Initially, rod of length \( L \) is placed between two supports at a distance \( L \) from each other. With no internal forces, there is no stress or strain.
    Force balance.
    $$ R_{A} = R_{B} = 0\ $$
    Reaction force.
    $$ R_{A} = F\ $$
    After raising the temperature, total elongation of the rod is still zero. The total elongation is given by:
    Total elongation.
    $$ \delta = \frac{FL}{EA} + \alpha L \Delta T = 0\ $$
    The stress in the rod due to change in temperature is given by:
    Stress from temperature changes.
    $$ \sigma = -\alpha E \Delta T\ $$

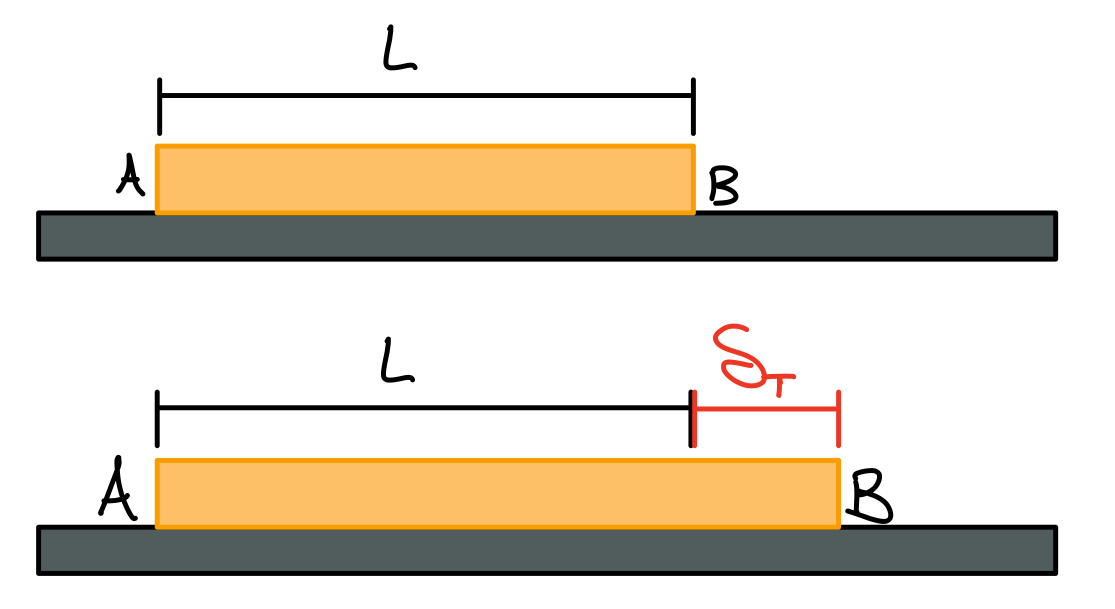
    Misfit Problems

    A misfit problem is one in which there is difference between a design distance and the manufactured length of a material. Some misfits are created intentionally to pre-strain a member. (e.g. spokes in a bicycle wheel or strings in a tennis racket). This type of problem neither modifies the equilibrium equations (1) nor the force-extension relations, (2) but the compatibility equations, (3) need to be modified.

    Heads up!

    Stress concentration factors build on this content in engineering materials and mechanical design.

    Stress concentraions

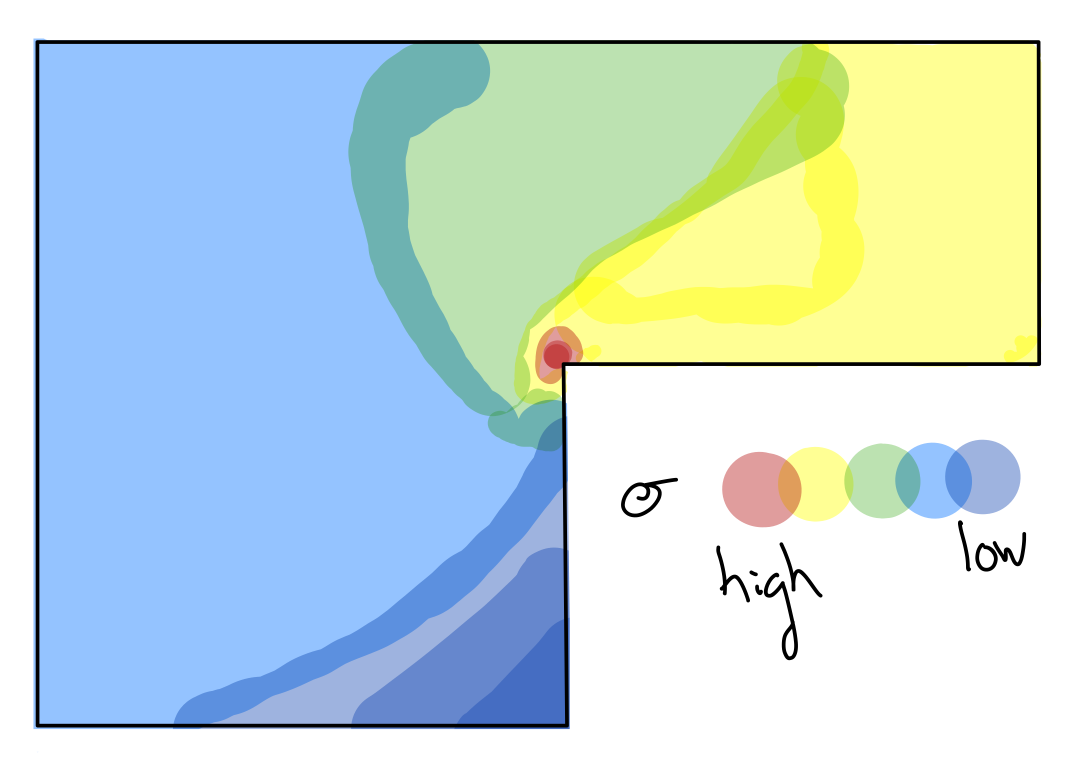
    The stress concentration factor is the highest at lowest cross-sectional area.

    Stress concentration factor.
    $$ K = \frac{\sigma_{max}}{\sigma_{avg}}\ $$

    • Found experimentally
    • Solely based on geometry