Force Systems
Equivalent systems
It can be helpful at times to reduce the forces on a body and combine resultant moments and simplify the analysis. For example, you can replace a force couple with their equivalent couple moment in a system. These forces and moments will have the same external effect on the body, but the internal forces on the rigid body may be different.Concentrated forces
Concentrated forces are forces acting at a specific point on a body. A concentrated force applied to a bar at point A.
Distributed loads
Distributed loads (usually written as \( w(x) \)) are forces applied over a length, volume, or area. The SI units for distributed loads are N/m. These loads, written as a function of length \( x \) can be simplified into an equivalent force, \( F_R \), which results in the same external loading on the rigid body. The magnitude of the equivalent force \( F_R \) is the area under the \( w(x) \) curve. The location of the resultant force \( F_R \) is the location of the centroid of the shape of the force curve.Rectangular loading
For a constant distributed load of magnitude c applied to a bar over a length l, the resultant force magnitude is Example distributed load (top) and its equivalent force system (bottom).
Triangular loading
For a triangular distributed load (a uniformly varying load), the magnitude of the load is equivalent to the area of the triangle. Example triangular distributed load (top) and its equivalent force system (bottom).
Nonuniform distributed loads
More complex distributed loads can be reduced to two distributed loads of uniform shape, or the integral of the distributed load function can be taken to obtain the area under \( w(x) \), which is \( F_R \).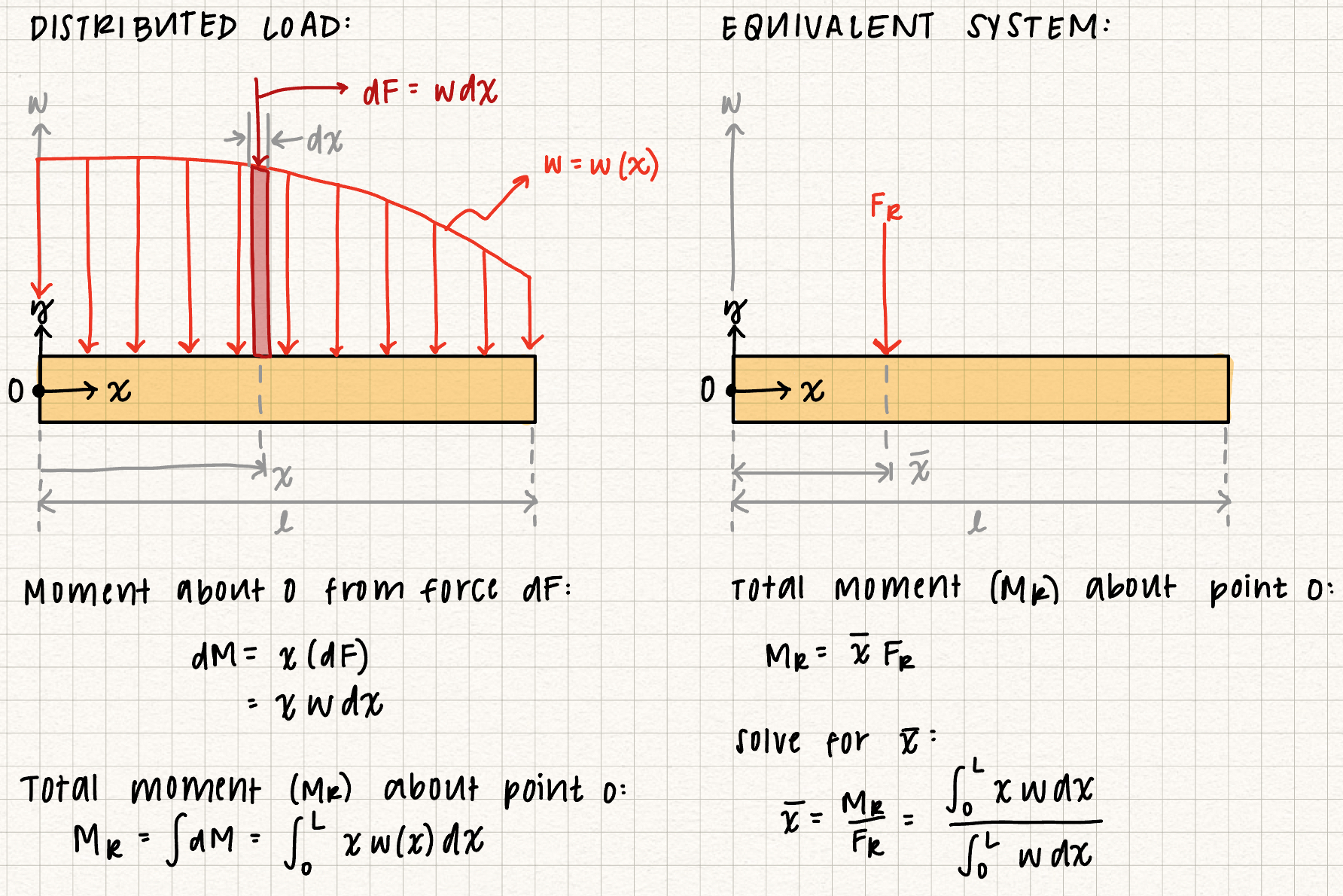
Nonuniform load.